| 恾俉丏侾丏侾 婘忋幚尡 |
 |
| | HOME | 栚師 | | 2009 (C) H.Ishikawa |
| 俉丏侾 | 婘忋偱幚尡偟偰傒傞 | ||
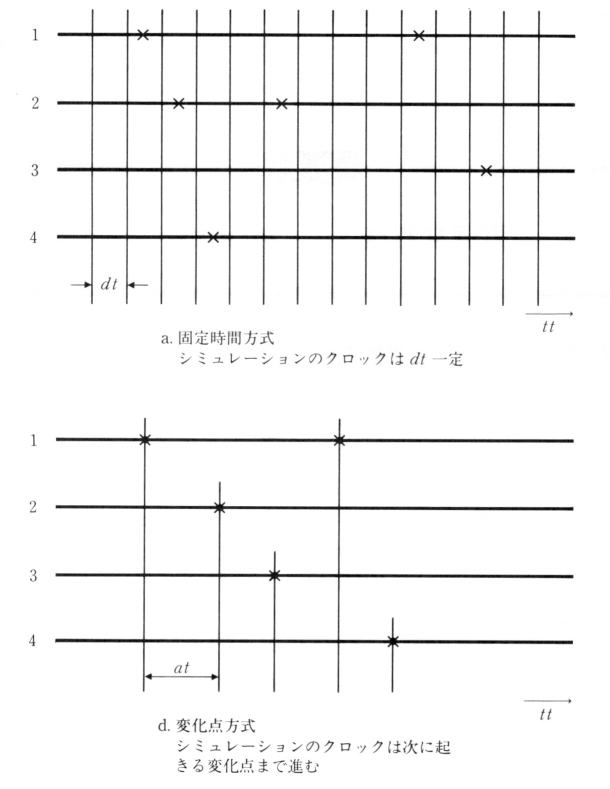
| 俉丏俀 | 僐儞僺儏乕僞偵傛傞椺戣偺僔儈儏儗乕僔儑儞亅亅屌掕帪娫曽幃亅亅 | ||
| 俉丏俁 | 崅懍側曽朄亅亅曄壔揰曽幃亅亅 | ||
| 俉丏係 | 偳偪傜偺僔儈儏儗乕僔儑儞曽幃偑偄偄偐 | ||
| 俉丏俆 | 僔儈儏儗乕僔儑儞帪娫偺寛傔曽 | ||
| 墘廗 |
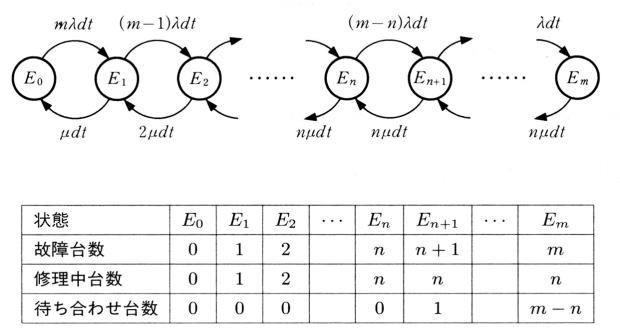
慜偺復傑偱偱丄偱偄偔偮偐偺娙扨側僔儈儏儗乕僔儑儞傪帋傒傑偟偨偑丄偦傟傜偼僐僀儞傪搳偘傞偲偐丄恓傪棊偲偡偲偐丄摨帪偵偼侾偮偺帠徾偟偐婲偙傜側偄応崌偱偟偨丅偟偐偟丄堦斒偵偼摨帪偵暲峴揑偵丄偄偔偮傕偺帠徾偑恑峴偡傞応崌偑偨偔偝傫偁傝傑偡丅偙偺摨帪恑峴偺僔儈儏儗乕僔儑儞傪峴側偆偵偼偳偆偟偨傜偄偄偱偟傚偆偐丅偙偺復偱偼丄婡夿廋棟偺栤戣偲偄偆丄暋悢偺婡夿偑偁傝丄暋悢偺廋棟幰偑偄傞偲偄偆丄摨帪恑峴偺揟宆揑側傕偺傪偲傝偁偘丄摨帪恑峴偺僔儈儏儗乕僔儑儞媄朄傪儅僗僞偡傞偙偲偲偟傑偡丅
俉丏侾丂婘忋偱幚尡偟偰傒傞
婡夿廋棟栤戣偲偼
丂崱偙偙偵丄m 戜偺惗嶻婡夿偑偁傞偲偟傑偡丅宱尡偐傜偡傞偲丄暯嬒 a 帪娫偡傞偲嬶崌偑埆偔側傝屘忈偟傑偡丅偦偺廋棟挷惍偼侾恖偺廋棟幰偵傛偭偰
h 帪娫偐偐傝傑偡丅惗嶻婡夿偼侾帪娫偁偨傝 r 墌偺廂塿乮廂擖乯偑偁傝丄廋棟幰偼侾恖偁偨傝侾帪娫
c 墌偺恖審旓偑偐偐傞傕偺偲偟傑偡丅壗恖偺廋棟幰傪梡堄偟廋棟偝偣傞偲丄棙塿乮廂塿儅僀僫僗旓梡乯偑嵟戝偲側傞偐丄偙傟偑婡夿廋棟偺栤戣偱偡1)丅
丂屘忈敪惗娫妘丄廋棟帪娫偦傟偧傟偑巜悢暘晍偺応崌丄棟榑揑夝愅偑壜擻偱偡偑2)丄偙偙偱偼偙傟傪僔儈儏儗乕僔儑儞偵傛傝夝愅偟偰傒傑偟傚偆丅
拲
1)丂僗僂僃乕僨儞偺岺嬈偱墳梡偝傟惉岟偟偰偄傞傕偺偲偟偰丄暥專(1)偵徯夘偑偁傞丅
2)丂俉丏係愡偵棟榑夝愅偺僾儘僌儔儉傪帵偡丅
婘忋幚尡
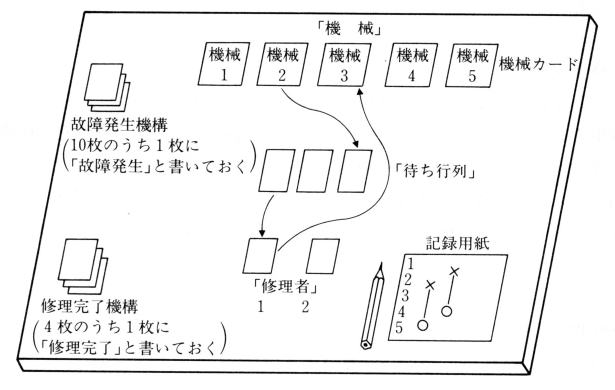
丂偙偺椺戣偺僔儈儏儗乕僔儑儞偼婡夿 m 戜丄廋棟幰n恖偑丄撈棫側摦偒傪偟傑偡偐傜丄偦偆娙扨偱偼偁傝傑偣傫丅僐儞僺儏乕僞傪梡偄傞慜偵丄婘忋幚尡傪僇乕僪傪梡偄偰帋傒偰摨帪摦嶌偺奣擮傪偮偐傓偙偲偲偟傑偟傚偆丅
丂婡夿偺戜悢 m=5 戜丄廋棟幰偺恖悢 n=2 恖丄屘忈偺暯嬒敪惗娫妘 a=10 帪娫丄暯嬒偺廋棟帪娫 h=4 帪娫偲壖掕偟傑偡丅
亙弨旛偡傞傕偺亜
丂屘忈敪惗婡峔丗侾侽枃偺僇乕僪丅偦偺偆偪偺侾枃偵乽屘忈敪惗乿偲彂偄偰偍偔乮侾侽帪娫偵侾夞屘忈偡傞偙偲傪丄堄枴偡傞乯丅
丂廋棟姰椆婡峔丗係枃偺僇乕僪丅偦偺偆偪偺侾枃偵乽廋棟姰椆乿偲彂偄偰偍偔乮廋棟帪娫偑係帪娫傪堄枴偡傞乯丅
丂婡夿僇乕僪丗俆枃偺僇乕僪丅婡夿偺斣崋侾乣俆傪彂偄偰偍偔丅
丂婰榐梡巻丗僔儈儏儗乕僔儑儞偺宱夁傪婰榐偡傞梡巻丅
亙婘忋僔儈儏儗乕僔儑儞亜
丂僔儈儏儗乕僔儑儞偺庤弴偼師偺偲偍傝偱偡丅
丂嘆丂弶婜愝掕
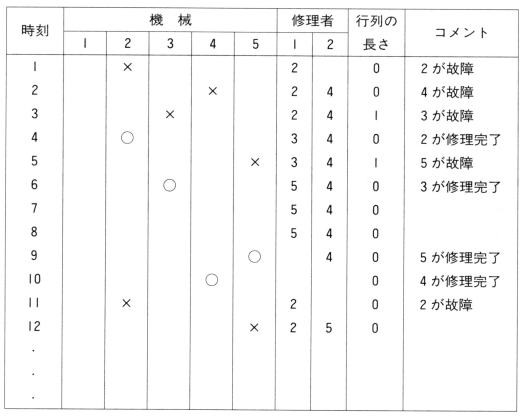
丂恾俉丏侾丏侾偺傛偆偵婘偺忋偺乽婡夿乿偺埵抲偵婡夿僇乕僪傪俆枃側傜傋傞丅傑偨乽懸偪峴楍乿偺埵抲丄乽廋棟幰乿偺埵抲傪嬻偗偰偍偔丅婰榐巻偵丄帪崗丄婡夿偺忬懺丄廋棟幰偑壗斣偺婡夿偺曐庣傪偟偰偄傞偐傪婰擖偱偒傞傛偆偵偟偰偍偔丅帪崗偼戞侾帪娫栚偲彂偄偰偍偔丅
丂嘇 屘忈敪惗
丂婡夿侾偺僇乕僪偑乽婡夿乿偺埵抲偵偍偄偰偁傟偽丄偦傟偼壱摥拞傪堄枴偟傑偡丅乽屘忈敪惗婡峔乿偺僇乕僪傪傛偔偒偭偰丄偦偺偆偪偺侾枃傪堷偔丅乽屘忈敪惗乿偺僇乕僪傪堷偄偨傜丄婡夿侾偺僇乕僪傪乽懸偪峴楍乿偺埵抲偵側傜傋傞丅婰榐梡巻偺侾帪娫栚偺婡夿侾偺棑偵亊乮屘忈敪惗偺儅乕僋乯傪偮偗傞丅
丂嘊丂屘忈敪惗孞曉偟
丂婡夿俀偐傜俆偵偮偄偰嘇傪孞傝曉偡丅
丂嘋 廋棟奐巒
丂師偵廋棟幰侾偺埵抲偵婡夿僇乕僪偑側偗傟偽丄偦偺廋棟幰偼廋棟拞偱側偄枹壱摥偺堄枴偱偁傞偺偱丄乽懸偪峴楍乿偺愭摢偺婡夿僇乕僪傪庢傝弌偟丄廋棟幰侾偺偲偙傠偵偍偔丅偦偟偰丄婰榐梡巻偺廋棟幰侾偺棑偵丄廋棟偡傞婡夿斣崋傪侾偲彂偄偰偍偔丅
丂嘍 廋棟姰椆
丂傕偟傕廋棟幰侾偺埵抲偵丄婡夿僇乕僪偑抲偄偰偁傟偽丄偦傟偼廋棟幰偑廋棟拞偱偁傞偙偲丄偮傑傝壱摥拞偑偁傞偙偲傪堄枴偟偰偄傞丅乽廋棟姰椆婡峔乿偺僇乕僪傪傛偔偒偭偰偦偺拞偐傜侾枃傪堷偔丅傕偟乽廋棟姰椆乿僇乕僪傪堷偄偨傜丄偦偺帪揰偱廋棟姰椆偱偁傞偐傜丄乽廋棟幰乿偺埵抲偵偁偭偨婡夿僇乕僪傪傕偲偺乽婡夿乿偺埵抲偵傕偳偡丅婰榐梡巻偺婡夿偺棑偵仜乮廋棟姰椆偺儅乕僋乯傪偮偗傞丅丂
丂嘐 廋棟姰椆孞曉偟
丂廋棟幰俀偵偮偄偰嘋嘍傪孞傝曉偡丅
丂嘑 埲忋偺帠偑丄侾帪娫偺拞偱摨帪偵婲偭偨帠偱偡丅帪寁傪侾帪娫恑傔丄嘇偐傜孞傝曉偡丅
丂埲忋偵傛傝丄悢廫帪娫暘傪孞傝曉偟丄婰榐梡巻傪尒傟偽丄昞俉丏侾丏侾偺傛偆偵側傞偱偟傚偆丅奺婡夿偑壗帪娫屘忈偱偁偭偨偐丄廋棟奐巒傑偱壗帪娫懸偨偝傟傞偐丄廋棟幰偼偳偺偔傜偄壱摥偟偰偄偨偐丄偙偺昞偐傜寁嶼偡傞偙偲偑偱偒傞偱偟傚偆丅
丂偙偺曽朄偼丄俁丏侾愡偱弎傋偨儀儖僰乕僀帋峴偺幚尡偺墳梡偱丄帪寁傪堦帪掆傔偰丄偡傋偰偺婡夿丄廋棟幰偵懳偟丄儀儖僰乕僀帋峴傪峴偭偨屻丄帪寁傪恑傔傞偲峫偊偰壓偝偄丅偙傟偑摨帪恑峴偺僔儈儏儗乕僔儑儞曽朄偱偡丅
| 恾俉丏侾丏侾 婘忋幚尡 |
 |
| 昞俉丏侾丏侾丂婰榐梡巻 |
 |
| 偙偺復巒傔 |
| 恾俉丏俀丏侾 婡夿廋棟栤戣偺忬懺慗堏恾 |
 |
| 恾俉丏俀丏俀 懸偪峴楍偺峔憿 |
 |
| 恾俉丏俀丏俁丂屌掕帪娫曽幃僔儈儏儗乕僔儑儞寢壥 (晹暘乯 |
 |
| S0820.java丂婡夿廋棟偺栤戣 (屌掕帪娫曽幃) 丂| Download | 幚峴 | |
/* S0820.java
* 婡夿廋棟偺栤戣 (屌掕帪娫曽幃)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.DecimalFormat;
public class S0820 extends Applet{
int M = 5; /* 婡夿偺戜悢 */
int N = 2; /* 廋棟幰偺恖悢 */
double A = 10.0; /* 暯嬒屘忈敪惗娫妘 */
double H = 4.0; /* 暯嬒廋棟帪娫 */
double DT = 0.5; /* 帪崗憹暘 */
double T_END = 30.0; /* 僔儈儏儗乕僔儑儞傪廔傞帪崗 */
public void paint(Graphics g) {
double tt = 0.0; /* 僔儈儏儗乕僔儑儞僋儘僢僋 */
int i; /* 懸偪峴楍偺for偺僇僂儞僞 */
int j; /* 婡夿偺for偺僇僂儞僞 */
int k; /* 廋棟幰偺for偺僇僂儞僞 */
int f = 0; /* 屘忈偟偰偄傞婡夿偺戜悢 */
int q = 0; /* 懸偪峴楍偺挿偝 */
int l = 0;
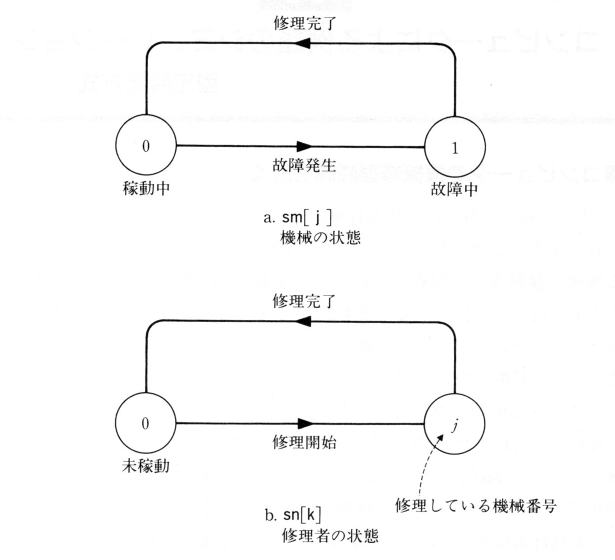
int sm[] = new int[M + 1]; /* 婡夿j偺忬懺 */
int sn[] = new int[N + 1]; /* 廋棟幰k偺忬懺 */
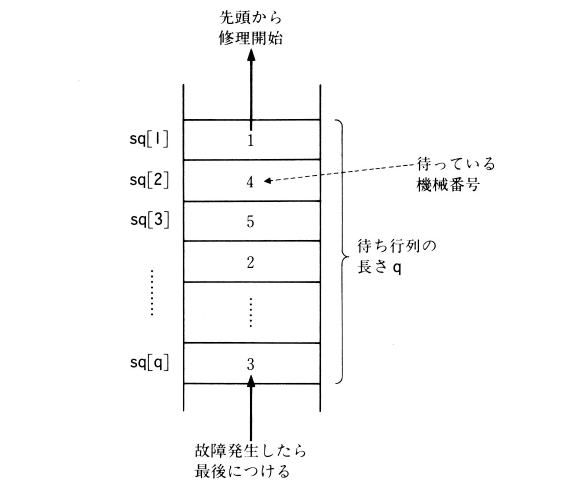
int sq[] = new int[M + 1]; /* 懸偪峴楍 */
double p[] = new double[M + 1]; /* 婡夿偑f戜屘忈偟偰偄傞帪娫偺妱崌 */
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
g.drawString(" tt sm[j] sn[k] sq[i]", 10, 10);
/* 奐巒 */
while (tt <= T_END) {
/* (1)屘忈敪惗 */
for (j = 1; j <= M; j ++) {
if (sm[j] == 0) { /* 婡夿偑壱摥拞側傜 */
if ((1.0 / A * DT) > Math.random()) { //(2)
sm[j] = 1; /* 偁傞妋棪偱屘忈偡傞 */
q = q + 1; /* (3)懸偪峴楍偺屻傠偵偮偔 */
sq[q] = j;
}
}
}
/* (4)屘忈廋棟 */
for (k = 1; k <= N; k ++) {
if (sn[k] == 0) { /* (5)廋棟幰偑枹壱摥側傜 */
if (q > 0) {
sn[k] = sq[1]; /* 懸偪峴楍偐傜庢傝弌偡 */
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i ++) {
sq[i] = sq[i + 1]; /* (6)懸偪峴楍傪1恑傔傞 */
}
}
}
} else {
if ((1.0 / H * DT) > Math.random()) { /* (7)廋棟幰偼婡夿傪廋棟偟 */
sm[sn[k]] = 0; /* 壱摥忬懺偵偡傞 */
sn[k] = 0;
}
}
}
/* (8)昞帵 */
g.drawString(" " + tt, 10, 20 + 10 * l);
for (j = 1; j <= M; j ++) g.drawString(" " + sm[j], 50 + 10 * j, 20 + 10 * l );
for (k = 1; k <= N; k ++) g.drawString(" " + sn[k], 100 + 10 * M +10 * k, 20 + 10 * l );
for (i = 1; i <= q; i ++) g.drawString(" " + sq[i], 150+ 10 * (M + N) + 10 * i, 20 + 10 * l );
l= l + 1;
/* 屘忈偟偰偄傞婡夿偺戜悢傪悢偊傞 */
f = 0;
for (j = 1; j <= M; j ++) {
if (sm[j] == 1) { f = f + 1; }
}
p[f] = p[f] + DT;
/* (9)帪崗傪恑傔傞 */
tt =tt + DT;
}
/* 寢壥弌椡 */
for (j = 0; j <= M; j ++) {
g.drawString("p["+ j + "]="+ " " + exFormat1.format((double)p[j] / T_END) ,10 , 20 + 10 * l + 10 * j);
}
}
}
|
| 偙偺復巒傔 |
| 恾俉丏俁丏侾丂屌掕帪娫曽幃偲曄壔揰曽幃 |
 |
| 恾俉丏俁丏俀丂曄壔揰曽幃僔儈儏儗乕僔儑儞寢壥 |
 |
| S0830.java丂婡夿廋棟偺栤戣 (曄壔揰曽幃) 丂| Download | 幚峴 | |
/* S0830.java
* 婡夿廋棟偺栤戣 (曄壔揰曽幃)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.DecimalFormat;
public class S0830 extends Applet{
int M = 5; /* 婡夿偺戜悢 */
int N = 2; /* 廋棟幰偺恖悢 */
double A = 10.0; /* 暯嬒屘忈敪惗娫妘 */
double H = 4.0; /* 暯嬒廋棟帪娫 */
double DT = 0.5; /* 帪崗憹暘 */
double T_END = 100.0; /* 僔儈儏儗乕僔儑儞傪廔傞帪崗 */
double INF = 1.0e100; /* 廫暘戝偒偄抣 */
double EPS = 1.0e-100; /* 廫暘彫偝偄抣 */
public void paint(Graphics g) {
double tt = 0.0; /* 僔儈儏儗乕僔儑儞僋儘僢僋 */
int i; /* 懸偪峴楍偺for偺僇僂儞僞 */
int j; /* 婡夿偺for偺僇僂儞僞 */
int k; /* 廋棟幰偺for偺僇僂儞僞 */
int f = 0; /* 屘忈偟偰偄傞婡夿偺戜悢 */
int q = 0; /* 懸偪峴楍偺挿偝 */
int l = 0; /* 昞帵峴 */
int sm[] = new int[M + 1]; /* 婡夿j偺忬懺 */
double tm[] = new double[M + 1]; /* (1)婡夿偵師偺忬懺曄壔偑婲傞傑偱偺帪娫 */
int sn[] = new int[N + 1]; /* 廋棟幰k偺忬懺 */
double tn[] = new double[N + 1]; /* (1)廋棟幰偵師偺忬懺曄壔偑婲傞傑偱偺帪娫 */
int sq[] = new int[M + 1]; /* 懸偪峴楍 */
double p[] = new double[M + 1]; /* (1)婡夿偑f戜屘忈偟偰偄傞帪娫偺妱崌 */
double at; /* 帪崗憹暘 */
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
DecimalFormat exFormat2 = new DecimalFormat(" 0.00");
g.drawString(" tt sm[j] sn[k] sq[i]", 10, 10);
/* (2)弶婜愝掕 */
for (j = 1; j <= M; j ++) {
sm[j] = 0; tm[j] = -A * Math.log(1 - Math.random());
}
for (k = 1; k <= N; k ++) {
sn[k] = 0; tn[k] = INF;
}
/* (3)奐巒 */
while (tt <= T_END) {
/* 屘忈敪惗 */
for (j = 1; j <= M; j ++) {
if (Math.abs(tm[j]) < EPS) { /* (4)婡夿j偑屘忈敪惗 */
sm[j] = 1; tm[j] = INF; /* (5) */
q = q + 1;
sq[q] = j;
}
}
/* (6)屘忈廋棟 */
for (k = 1; k <= N; k ++) {
if (Math.abs(tn[k]) < EPS) { /* (7)廋棟幰k偺廋棟偑姰椆 */
sm[sn[k]] = 0; tm[sn[k]] = -A * Math.log(1 - Math.random()); /* (8) */
}
if (Math.abs(tn[k]) <EPS || sn[k] == 0) { /* (9)k偑枹壱摦偺応崌 */
if (q > 0) { /* (10)懸偪峴楍傪庢傝弌偡 */
sn[k] = sq[1]; tn[k] = -H * Math.log(1 - Math.random());
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i ++) {
sq[i] = sq[i + 1];
}
}
} else { /* 懸偪峴楍偑嬻側傜廋棟幰k偼枹壱摥忬懺偵側傞 */
sn[k] = 0; tn[k] = INF;
}
}
}
/* (13)昞帵 */
g.drawString(" " + exFormat2.format(tt), 10, 20 + 10 * l);
for (j = 1; j <= M; j ++) g.drawString(" " + sm[j], 50 + 10 * j, 20 + 10 * l );
for (k = 1; k <= N; k ++) g.drawString(" " + sn[k], 100 + 10 * M +10 * k, 20 + 10 * l );
for (i = 1; i <= q; i ++) g.drawString(" " + sq[i], 150+ 10 * (M + N) + 10 * i, 20 + 10 * l );
l= l + 1;
/* (11)師偵忬懺曄壔偺婲傞帪崗傪媮傔傞 */
at = INF;
for (j = 1; j <= M; j ++) {
if (tm[j] < at) at = tm[j];
}
for (k = 1; k <= N; k++) {
if (tn[k] < at) at = tn[k];
}
/* (14)屘忈偟偰偄傞婡夿偺戜悢傪悢偊傞 */
f = 0;
for (j = 1; j <= M; j ++) {
if (sm[j] == 1) { f ++; }
}
p[f] = p[f] + at;
/* (12)帪娫傪恑傔傞 */
for (j = 1; j <= M; j ++) {
tm[j] = tm[j] - at;
}
for (k = 1; k <= N; k ++) {
tn[k] = tn[k] - at;
}
tt = tt+ at;
}
/* 寢壥弌椡 */
for (j = 0; j <= M; j ++) {
g.drawString("p["+ j + "]="+ " " + exFormat1.format((double)p[j] / T_END) ,10 , 20 + 10 * l + 10 * j);
}
}
}
|
| 偙偺復巒傔 |
俉丏係丂偳偪傜偺僔儈儏儗乕僔儑儞曽幃偑偄偄偐
| 恾俉丏係丏侾 |
 |
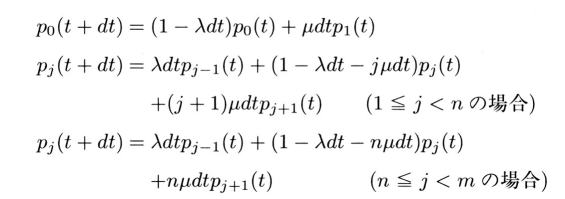 |
丒丒丒 | 幃俉丏係丏侾 |
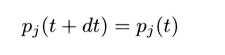 |
丒丒丒丒丒 | 幃俉丏係丏俀幃 |
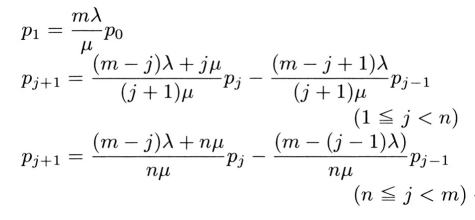 |
丒丒丒 | 幃俉丏係丏俁 |
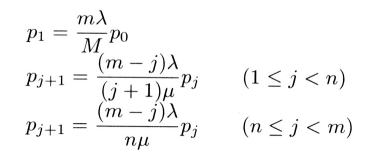 |
丒丒丒 | 幃俉丏係丏係 |
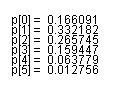
| 恾俉丏係丏俀丂S0840.java偺 寢壥 |
 |
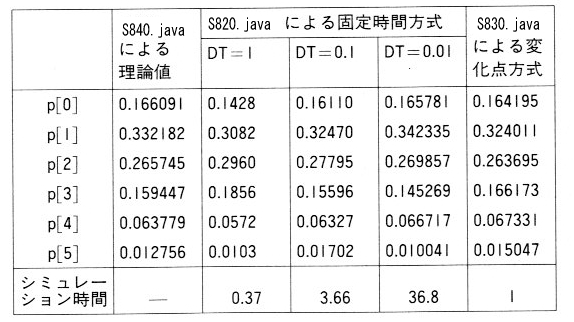
| 昞俉丏係丏侾 屌掕帪娫曽幃偲曄壔揰曽幃偺斾妑 |
 |
| S0840.java丂婡夿廋棟偺栤戣 (棟榑抣) 丂| Download | 幚峴 | |
/* S0840.java
* 婡夿廋棟偺栤戣 (棟榑抣)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.DecimalFormat;
public class S0840 extends Applet{
int M = 5; /* 婡夿偺戜悢 */
int N = 2; /* 廋棟幰偺恖悢 */
double A = 10.0; /* 暯嬒屘忈敪惗娫妘 */
double H = 4.0; /* 暯嬒廋棟帪娫 */
public void paint(Graphics g) {
int j; /* 婡夿偺for偺僇僂儞僞 */
double p[] = new double[M + 1]; /* 婡夿偑f戜屘忈偟偰偄傞帪娫偺妱崌 */
double p0 = 0.0;
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
p[0] = 1;
p[1] = (double)M * H / A * p[0];
for (j = 1; j <= N - 1; j ++) {
p[j + 1] = (double)(M - j) / (j + 1) * H / A * p[j];
}
for (j = N; j <= M - 1; j ++) {
p[j + 1] = (double)(M - j) / N * H / A * p[j];
}
for (j = 0; j<= M; j ++) {
p0 = p0 + p[j];
}
for (j = 0; j<= M; j ++) {
p[j] = p[j] / p0;
}
for (j = 0; j <= M; j ++) {
g.drawString("p["+ j + "] ="+ " " + exFormat1.format(p[j] ) ,10 , 20 + 10 * j);
}
}
}
|
| 偙偺復巒傔 |
俉丏俆丂僔儈儏儗乕僔儑儞帪娫偺寛傔曽
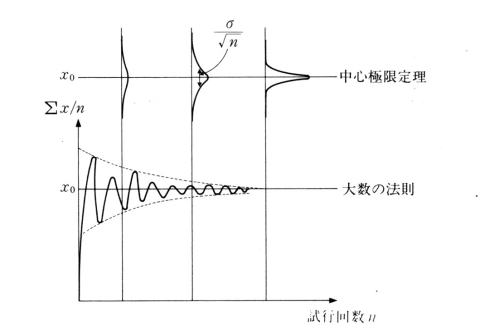
丂僔儈儏儗乕僔儑儞傪偍偙側偆応崌丆怣棅偵懌傞寢壥傪摼傞偺偵偳偺偔傜偄寁嶼婡傪夞偡偺偑昁梫偱偟傚偆偐丅JAVA傾僾儗僢僩傪巊偊偽丄嵟廔寢壥傪傾僂僩僾僢僩偡傞偺傒側傜偢丆搑拞偺宱夁傪僨傿僗僾儗僀偡傞偙偲偑偱偒傑偡偐傜丆偦偺宍傪傒偰丆廂懇忬嫷傪丆敾掕偡傞偙偲偑偱偒傑偡丅
丂僨傿僗僾儗僀偺夋柺偵偼丆墶幉偵帋峴夞悢偁傞偄偼僔儈儏儗乕僔儑儞僋儘僢僋丆廲幉偵寢壥傪偲傞偲丆恾俉丏俆丏侾偺傛偆側僌儔僼偑昞帵偝傟傞偱偟傚偆丅偡側傢偪丆巒傔偼偽傜偮偒偑戝偒偔丆偟偩偄偵丆廂懇偝傟偰峴偒傑偡丅俁丏係愡偺戝悢偺朄懃偲丆俁丏俆愡偺拞怱嬌尷掕棟傪丆巚偄偩偟偰壓偝偄丅廲幉偼偁傞帋峴偺寢壥丆惉岟偺夞悢偲帋峴偺夞悢偺斾偱偡偐傜丆戝悢偺朄懃偵傛傝丆帋峴夞悢
n 傪懡偔偡傞偲堦掕抣偵嬤偯偔傢偗偱偡丅偟偐傜偽丆偙偺応崌偺僶儔僣僉偼偳偆偱偟傚偆偐丅拞怱嬌尷掕棟偼丆丂x丂偺暘晍偵偐偐傢傜偢丆丂x丂傪丂n丂屄崌寁偟丆丂n丂偱妱傞偲丆昗弨曃嵎偑丆丂侾乛併n丂偺惓婯暘晍偲側傞偲偄偭偰偄傑偡丅丂n丂傪戝偒偔偡傞偲昗弨曃嵎偼彫偝偔拞怱偵嬤偢偔傢偗偱偡丅偟偐偟丆偦偺妱崌偼丂n丂傪丆侾侽侽攞偟偰傕丆昗弨曃嵎偼丆侾乛侾侽偵偟偐側傝傑偣傫丅偮傑傝丆侾寘惛搙傪忋偘傛偆偲偡傟偽丆僔儈儏儗乕僔儑儞帪娫傪侾侽侽攞偐偗傞昁梫偑偁傝傑偡丅
| 恾俉丏俆丏侾丂僔儈儏儗乕僔儑儞帪娫偲寢壥偺廂懇 |
 |
| 偙偺復巒傔 |
侾丏丂婡夿偺戜悢亖俆戜丄屘忈偺暯嬒敪惗娫妘亖侾侽帪娫丄暯嬒廋棟帪娫亖係帪娫丄侾帪娫偁偨傝偺婡夿侾戜偺廂塿亖俉枩墌丄廋棟幰侾恖侾帪娫偁偨傝偺旓梡亖俀枩墌偲偟偨偲偒丄嵟戝棙塿偑摼傜傟傞棟榑揑側廋棟幰偺恖悢傪媮傔側偝偄丅
丂丂乮夝摎乯丂丂A0810.java 丂| 幚峴 |
丂丂丂丂丂丂丂丂偙傟偵傛傟偽丄俀恖偑嵟椙
俀丏丂僾儘僌儔儉S0830.java偱丄廋棟帪娫傪埵憡k=3偺傾乕儔儞暘晍偲偟偨応崌偵偮偄偰丄僔儈儏儗乕僔儑儞偟側偝偄丅
丂丂乮夝摎乯丂丂A0820.java 丂| 幚峴 |
俁丏丂僾儘僌儔儉S0830.java傪夵憿偟偰丄屘忈偟偰偄傞婡夿偺妱崌 pf[j]/tt 傪丄帪乆崗乆昞帵偟丄僔儈儏儗乕僔儑儞偺廂懇忬嫷傪丄娤應偱偒傞傛偆偵偟側偝偄丅傑偨婡夿偺壱摥棪丄廋棟幰偺壱摥棪丄婡夿偺懸偪帪娫偺暘晍丄婡夿偺懸偪崌傢偣暯嬒帪娫丄偦偺暘嶶傪媮傔傞傛偆偵偟側偝偄丅
丂丂乮夝摎乯丂丂A0830.java 丂| 幚峴 |
係丏丂侾杮偺摦椡慄傪 m 恖偺梟愙岺偑嫟梡偟偰偄傑偡丅梟愙岺偼儔儞僟儉偵抐懕揑偵侾俙偺揹棳傪巊梡偟傑偡丅偦偺帪娫偺暯嬒抣偼 h 暘偱娫妘偺暯嬒偼 a 暘偱偡丅揹棳偺攇宍傪僔儈儏儗乕僔儑儞偟側偝偄丅
丂丂乮夝摎乯丂丂A0840.java 丂| 幚峴 |
| 偙偺復巒傔 |
| | HOME | 栚師 | | 2009 (C) H.Ishikawa |