| 図4.1.1 区間[a, b)の一様分布 |
 |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |
| 4.1 | 区間を決めた一様分布の乱数を作る−−区間一様乱数−− | ||
| 4.2 | 指数分布の乱数を作る−−指数乱数−− | ||
| 4.3 | ポアソン分布の乱数発生方法−−ポアソン乱数−− | ||
| 4.4 | アーラン乱数を作る −アーラン乱数− | ||
| 4.5 | 正規分布の乱数を作る −正規乱数− | ||
| 4.6 | 任意の分布の乱数を作る | ||
| 演習 |
第2章で、一様乱数を発生させるMath.random()メソッドについて学びました。システム・シミュレーションにおいては、一様乱数のみならず、さまざまな分布の乱数を用いることがあります。本章では、一様乱数を変換してさまざまな分布の乱数を作り出す手法を学びます。
逆関数法
Math.random()メソッドで得られる乱数は、0と1の間、すなわち、区間 [0,1) ですが、それを区間 [a.b) のような特定区間の一様乱数を得るにはどうしたらよいのでしょうか。
一般に、区間 [0,1) の一様乱数から特定区間の一様乱数を得るには、次の逆関数法がよく使われます。
区間 [0,1) の一様乱数の確率密度関数 f(x) は、図4.1.1aのようになります(注)。これを積分した分布関数 g(x) は図4.1.1bのようになります。 g(x) の値は0から1の値をとりますから、区間 [0,1) の一様乱数を発生させ、 g(x) の逆関数(図4.1.1bの縦軸)に代入すれば、区間 [a, b) の乱数が得られます。これを逆関数法による乱数の変換といいます。
| 図4.1.1 区間[a, b)の一様分布 |
 |
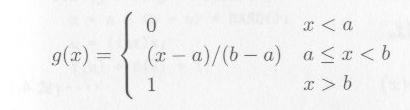 |
・・・・・ | 式4.1.1 |
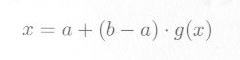 |
・・・・・ | 式4.1.2 |
| 図4.1.2 区間一様乱数の発生結果 |
 |
| S0410.java 区間一様乱数の発生 | Download | 実行 | |
/* S0410.java
* 区間一様乱数の発生
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0410 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int NUMBER = 10000;
int SIZE = 20; /* ヒストグラムの大きさ */
int j; /* forのカウンタ */
int u; /* xの整数部分 */
double x; /* 一様乱数n個の合計 */
double a = 5; /* 一様分布の下限 */
double b = 15; /* 一様分布の上限 */
int f[] = new int[SIZE]; /* 頻度 */
/* グラフィックの準備 */
int SPACE = 40;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0,0.0,20,0.1501, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "x",1, "f[x] / NUMBER", 0.050,g);
/*メイン*/
for (j = 0; j < NUMBER; j ++) {
x = a + (b - a) * Math.random();
u = (int)x;
f[u] = f[u] + 1;
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < SIZE; u ++) {
w.line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER,g);
}
}
}
|
| この章始め |
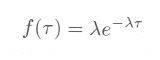 |
・・・・・ | 式4.2.1 |
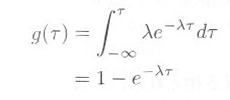 |
・・・・・ | 式4.2.2 |
| 図4.2.1 指数分布 |
 |
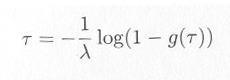 |
・・・・・ | 式4.2.3 |
| 図4.2.2 指数乱数の発生結果 |
 |
| S0420.java 指数乱数の発生 | Download | 実行 | |
/* S0420.java
* 指数乱数の発生
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0420 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int NUMBER = 10000;
int j; /* forのカウンタ */
int u; /* τの整数部分 */
int f[] = new int[100]; /* uの頻度 */
double tau; /* τ */
double lambda = 1; /* λ */
/* グラフィックの準備 */
int SPACE = 40;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0,0.0,15,0.8, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "tau", 1, "f[tau] / NUMBER", 0.1,g);
/*メイン*/
for (j = 0; j <= NUMBER; j++) {
tau = -1.0 / lambda * Math.log(1.0 - Math.random());
u = (int)tau;
f[u] = f[u] + 1;
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < 15; u ++) {
w.line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER, g);
}
}
}
|
| この章始め |
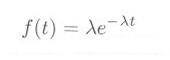 |
・・・・・ | 式4.3.1 |
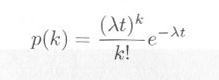 |
・・・・・ | 式4.3.2 |
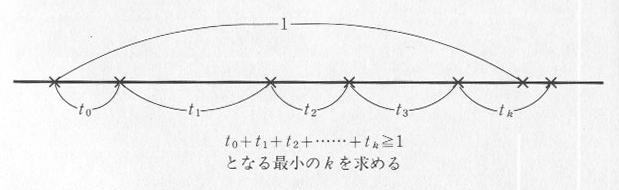
| 図4.3.1 ポアソン乱数の作り方 |
 |
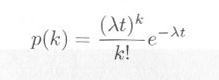 |
・・・・・ | 式4.3.2 |
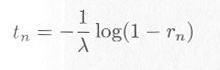 |
・・・・・ | 式4.3.4 |
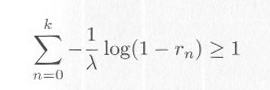 |
・・・・・ | 式4.3.5 |
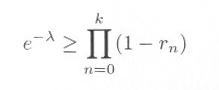 |
・・・・・ | 式4.3.6 |
S0430.javaの実行結果を図4.3.2に示します。
| 図4.3.2 ポアソン乱数の発生結果 |
 |
| S0430.java ポアソン乱数の発生 | Download | 実行 | |
/* S0430.java
* ポアソン乱数の発生
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0430 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int NUMBER = 10000;
int SIZE = 20; /* ヒストグラムの大きさ */
int j; /* forのカウンタ */
int k; /* 本文kの説明参照 */
int f[] = new int [SIZE]; /* kの頻度 */
double lambda = 1; /* λ */
/* グラフィックの準備 */
int SPACE = 40;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0,0.0,SIZE,0.5, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "k", 1, "f[k] / NUMBER", 0.1,g);
/*メイン*/
for (j = 0; j < NUMBER; j++) {
k = poisson(lambda);
f[k] = f[k] + 1;
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (k = 0; k < SIZE; k ++) {
w.line(0, k + 0.5, 0, k + 0.5, (double)f[k] / NUMBER, g);
}
}
int poisson(double lambda) {
double xp;
int k = 0;
xp = Math.random();
while (xp >= Math.exp(-lambda)) {
xp = xp * Math.random();
k = k + 1;
}
return (k);
}
}
|
| この章始め |
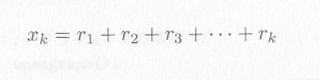 |
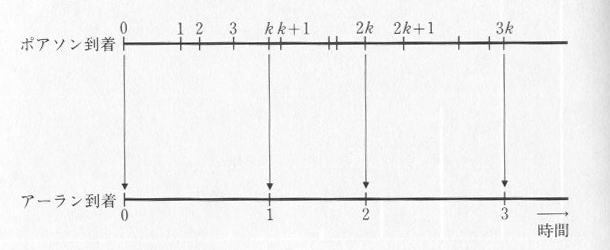
| 図4.4.1 ポアソン到着と位相 k のアーラン到着 |
 |
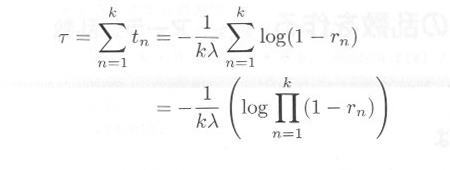 |
・・・・・ | 式4.4.1 |
| 図4.4.2 アーラン乱数の発生結果 |
 |
| S0440.java アーラン乱数の発生 | Download | 実行 | |
/* S0440.java
* アーラン乱数の発生
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0440 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int NUMBER = 1000;
int SIZE = 20; /* ヒストグラムの大きさ */
double KIZAMI = 0.2; /* 0.2ずつに区切ってヒストグラムへ */
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int i; /* forのカウンタ */
int f[] = new int[SIZE]; /* 頻度 */
int k = 1; /* 位相 k=1,2,4,8,16 */
double lambda = 1; /* λ */
/* グラフィックの準備 */
int SPACE = 40;
int HIGHT = 640;
int WIDTH = 640;
w.setWindow(0, 0.0,0.0,4.001,0.4,SPACE,HIGHT/5-SPACE,WIDTH-SPACE,0);
w.axis(0, "", 0.2, "k = 1", 0.1,g);
w.setWindow(1, 0.0,0.0,4.001,0.4,SPACE,2*HIGHT/5-SPACE,WIDTH-SPACE,HIGHT/5);
w.axis(1, "", 0.2, "k = 2", 0.1, g);
w.setWindow(2, 0.0,0.0,4.001,0.4,SPACE,3*HIGHT/5-SPACE,WIDTH-SPACE,2*HIGHT/5);
w.axis(2, "", 0.2, "k = 4", 0.1,g);
w.setWindow(3, 0.0,0.0,4.001,0.4,SPACE,4*HIGHT/5-SPACE,WIDTH-SPACE,3*HIGHT/5);
w.axis(3, "", 0.2, "k = 8", 0.1,g);
w.setWindow(4, 0.0,0.0,4.001,0.4,SPACE,HIGHT-SPACE,WIDTH-SPACE,4*HIGHT/5);
w.axis(4, "", 0.2, "k = 16", 0.1,g);
/* メイン */
for (i = 0; i < 5; i ++) {
for (j = 0; j < NUMBER; j++) {
u = (int)(erlang(lambda, k) / KIZAMI);
if (u < SIZE) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < SIZE; u ++) {
w.line(i, (u+0.5) * KIZAMI, 0, (u+0.5) * KIZAMI, (double)f[u] / NUMBER, g);
f[u] = 0;
}
k = k * 2; /* 2倍のkの値で続ける */
}
}
double erlang(double lambda, int k){
double tp = 1.0;
double tau;
int n;
for (n = 1; n <= k; n ++) {
tp = tp * (1 - Math.random());
}
tau = -1.0 / lambda / (double)k * Math.log(tp);
return (tau);
}
}
|
| この章始め |
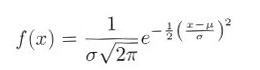 |
・・・・・ | 式4.5.1 |
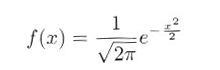 |
・・・・・ | 式4.5.2 |
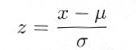 |
・・・・・ | 式4.5.3 |
| 図4.5.1 正規分布 |
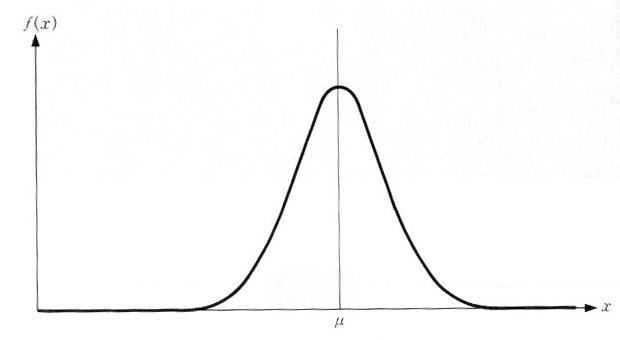 |
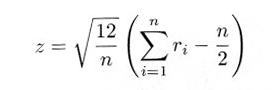 |
・・・・・ | 式4.5.4 |
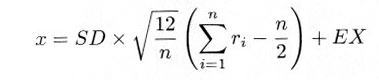 |
・・・・・ | 式4.5.5 |
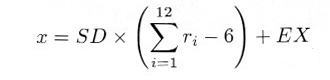 |
・・・・・ | 式4.5.6 |
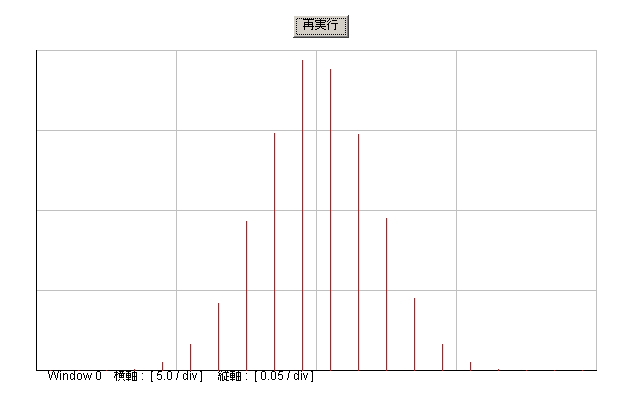
S0450.javaの実行結果を図4.5.2に示します。
| 図4.5.2 正規乱数の発生結果 |
 |
| S0450.java 正規乱数の発生 | Download | 実行 | |
/* S0450.java
* 正規乱数の発生
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0450 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int NUMBER = 10000;
int SIZE = 20; /* ヒストグラムの大きさ */
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int f[] = new int [SIZE]; /* ヒストグラム */
double ex = 10; /* 平均値 */
double sd = 2; /* 標準偏差 */
/* グラフィックの準備 */
int SPACE = 40;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0,0.0,20.0,0.2, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "", 5, "", 0.05,g);
/* メイン */
for (j = 0; j < NUMBER; j++) {
u = (int)(normal(ex, sd));
if (u >= 0 || u < SIZE) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < SIZE; u ++) {
w.line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER, g);
}
}
double normal(double ex, double sd){
double xw = 0.0;
double x;
int n;
for (n = 1; n <= 12; n ++) { /* 12個の一様乱数の合計 */
xw = xw + Math.random();
}
x = sd * (xw - 6.0) + ex;
return (x);
}
}
|
| この章始め |
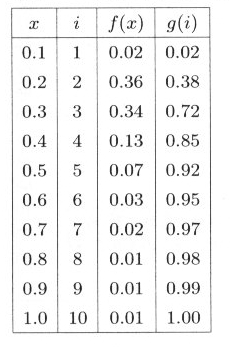
| 表4.6.1 与えられた度数分布 |
 |
| 図4.6.1 累積分布の逆関数による乱数発生 |
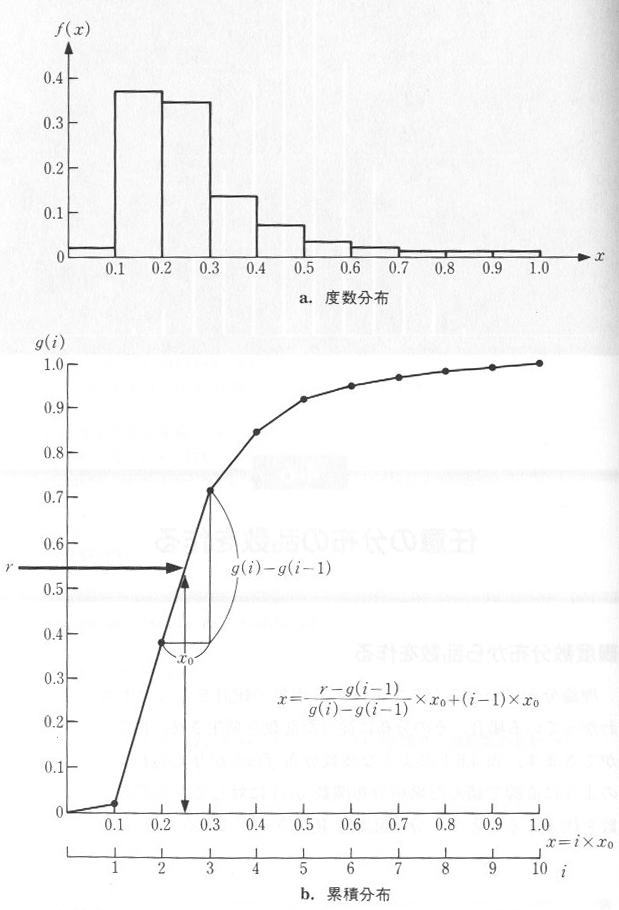 |
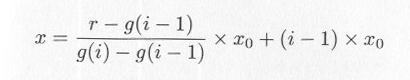 |
・・・・・ | 式4.6.1 |
| 図4.6.2 任意分布乱数の発生結果 |
 |
| S0460.java 任意分布乱数の発生 | Download | 実行 | |
/* S0460.java
* 任意分布乱数の発生
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0460 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
int SIZE = 10; /* ヒストグラムの大きさ */
public void paint(Graphics g){
Window w ;
w = new Window();
int NUMBER = 10000;
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int f[] = new int [SIZE]; /* ヒストグラム */
/* グラフィックの準備 */
int SPACE = 40;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0,0.0,10.0,0.4, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "", 1, "", 0.05,g);
/* メイン */
for (j = 0; j <= NUMBER; j++) {
u = (int)(general() * SIZE);
if (u >= 0) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < SIZE; u ++) {
w.line(0, u+0.5, 0, u+0.5, (double)f[u] / NUMBER, g);
}
}
double general() {
double g[]= {0.0,0.02,0.38,0.72,0.85,0.92,0.95,0.97,0.98,0.99,1.0};
double x0 = 1.0 / SIZE;
double r,x;
int i = 0;
r = Math.random();
while (g[i] < r) {
i = i + 1;
}
x = (r - g[i - 1]) / (g[i] - g[i - 1]) * x0 + (i - 1) * x0;
return (x);
}
}
|
| この章始め |
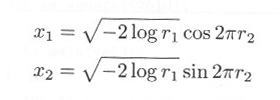 |
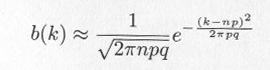 |
| この章始め |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |