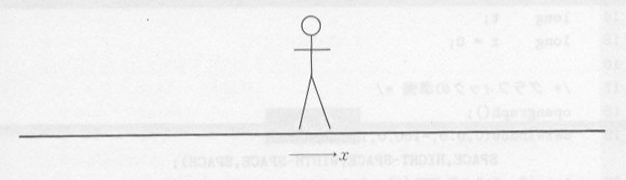
| 図6.1.1 1次元ランダムウォーク |
 |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |
| 6.1 | 1次元ランダムウォーク | ||
| 6.2 | 2次元ランダムウォークのシミュレーション | ||
| 6.3 | 拡散のシミュレーション | ||
| 6.4 | ほこりはすみにたまる | ||
| 演習 |
液体や気体中に浮遊する微粒子は、不規則な運動をくりかえしています。この現象は、1827年に植物学者ブラウンによって、水に浮く花粉の不規則な運動として初めて発見されました。この現象は、酔っぱらいが、ちどり足で歩くのとにていることから、ランダムウォークあるいは酔歩の問題と呼ばれます。
6.1 1次元ランダムウォーク
1次元ランダムウォーク
まずはじめに、簡単な1次元のランダムウォークを考えてみます。図6.1.1のように1本の道の上で、酔っぱらいが、ふらふらといったりきたりしているとします。
| 図6.1.1 1次元ランダムウォーク |
 |
酔っぱらいが、ある時刻で x の場所にいたとして、次の時刻に前へ行くか、後ろへ行くかは、まったくランダムで、予測が着きません。このような場合の、 x について、シミュレーションしてみましょう。
プログラムのポイント
プログラムS0610.javaは、1次元ランダムウォークのシミュレーション・プログラムで、各クロックごとに、(1)において確率1/2で、前へ進むか、後ろに進むかをきめています。その結果を図6.1.2に示します。横軸時刻
t 、縦軸 x のグラフとして表現しています。このランダムウォークは、3.1節でのべたベルヌーイ試行を時刻 t ごとにおこなっているものです。
またこれは、勝ったり負けたりのゲームで、持ち金の金額の変化をあらわしています。
| 図6.1.2 1次元ランダムウォークのシミュレーション結果 |
 |
| S0610.java 1次元ランダムウォーク | Download | 実行 | |
/* S0610.java
* 1次元ランダムウォーク
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0610 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g) {
Window w ;
w = new Window();
int SPACE = 30;
int HIGHT = 400;
int WIDTH = 640;
long t = 0;
long x = 0;
long T_END = 1000; /* 終りの時刻 */
double P = 0.5; /* 確率1/2 */
/*グラフィックの準備*/
w.setWindow(0, 0.0,-100.0,T_END,100.0, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "t", T_END/10, "x", 10, g);
w.moveTo(0, 0.0, 0.0, g);
/*メイン*/
for (t = 0; t < T_END; t ++) {
if (P > Math.random()) { //(1) 確率1/2で前へ進むか、後ろに進むか
x = x + 1;
} else {
x = x - 1;
}
g.setColor(Color.green);
w.lineTo(0, (double)(t), (double)(x), g);
}
stop();
}
}
|
| この章始め |
| 図6.2.1 2次元ランダムウォーク |
 |
| 図6.2.2 2次元ランダムウォークのシミュレーション結果 |
 |
| S0620.java 2次元ランダムウォーク | Download | 実行 | |
/* S0620.java
* 2次元ランダムウォーク
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0620 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g) {
Window w ;
w = new Window();
int SPACE = 30;
int HIGHT = 400;
int WIDTH = 640;
double X_MAX = 80.0;
double Y_MAX = 50.0;
double x,y; /* 粒子の座標 */
double th; /* θ */
int t; /*時刻*/
long T_END = 10000; /* 終りの時刻 */
/*グラフィックの準備*/
w.setWindow(0, -X_MAX, -Y_MAX, X_MAX, Y_MAX, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
w.axis(0, "", 10,"", 10, g);
w.moveTo(0, 0, 0, g);
/*メイン*/
x = 0.0;
y = 0.0;
for (t = 1; t <= T_END; t ++) {
th = 2.0 * Math.PI * Math.random(); //(1)
x = x + Math.cos(th); //(2)
y = y + Math.sin(th); //(2)
g.setColor(Color.green);
w.lineTo(0, x, y, g); //(3)
}
stop();
}
}
|
| この章始め |
拡散過程 (文献(10)参照)
 |
・・・ | 式6.3.1 |
| ・・・・・ | 式6.3.2 |
| 図6.3.1 粒子の位置 |
 |
| 図6.3.2 拡散のシミュレーション結果(途中の図 長時間CPU占有注意) |
 |
| S0630.java 拡散のシミュレーション | Download | 実行 (長時間CPU占有注意)| |
/* S0630.java
* 拡散のシミュレーション
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0630 extends Applet implements ActionListener {
Button button0;
Button button1;
int sw =0;
public void init() {
button0 = new Button(" 実行 ");
button1 = new Button("クリア");
add(button0);
add(button1);
button0.addActionListener(this);
button1.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
if (label.equals(" 実行 ")) sw = 1; else sw = 0;
repaint();
}
public void paint(Graphics g) {
Window w ;
w = new Window();
int SPACE = 30;
int HIGHT = 400;
int WIDTH = 640;
int PARTICLE = 10000; /* 粒子の数 */
double MAX = 50.0;
long T_END = 1000;
double x[] = new double[PARTICLE]; /* すべての粒子は原点にある */
double y[] = new double[PARTICLE];
int i; /* 粒子のカウンタ */
long t = 0; /* 時刻 */
double th; /* θ */
double d1; /* 原点からの距離の和 */
double d; /* 原点からの距離の平均値 */
/*グラフィックの準備*/
w.setWindow(0, -MAX,-MAX,MAX,MAX, SPACE,HIGHT-SPACE,HIGHT-SPACE,SPACE);
w.axis(0, "", MAX, "", MAX, g);
w.setWindow(1, 0,0,T_END,MAX, HIGHT,HIGHT/2,WIDTH-SPACE,SPACE);
w.axis(1, "時間", T_END / 5, "原点からの平均距離", MAX / 5, g);
w.moveTo(1, 0.0, 0.0, g);
/*メイン*/
if ( sw == 1) {
while (t < T_END) {
d1 = 0.0;
for (i = 0; i < PARTICLE; i ++) {
th = 2.0 * Math.PI * Math.random();
if (x[i] <= MAX && x[i] >= -MAX && y[i] <= MAX && y[i] >= -MAX) {
g.setColor(Color.white);
w.putPixel(0, x[i], y[i], g);} /* 前の粒子の位置を消す */
x[i] = x[i] + Math.cos(th);
y[i] = y[i] + Math.sin(th);
if (x[i] <= MAX && x[i] >= -MAX && y[i] <= MAX && y[i] >= -MAX) {
g.setColor(Color.blue);
w.putPixel(0, x[i], y[i], g); } /* 次の粒子の位置を表示 */
d1 = d1 + Math.sqrt(x[i] * x[i] + y[i] * y[i]);
}
w.axis(0, "",MAX,"",MAX, g); /* 消された軸を再度書く */
d = (double)(d1 / PARTICLE);
t = t + 1;
w.lineTo(1, t, d, g);
}
stop();
}
}
}
|
| この章始め |
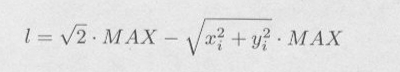 |
・・・・・ | 式6.4.1 |
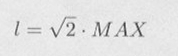 |
・・・・・ | 式6.4.2 |
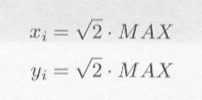 |
・・・・・ | 式6.4.3 |
| 図6.4.1 粒子の動き方 |
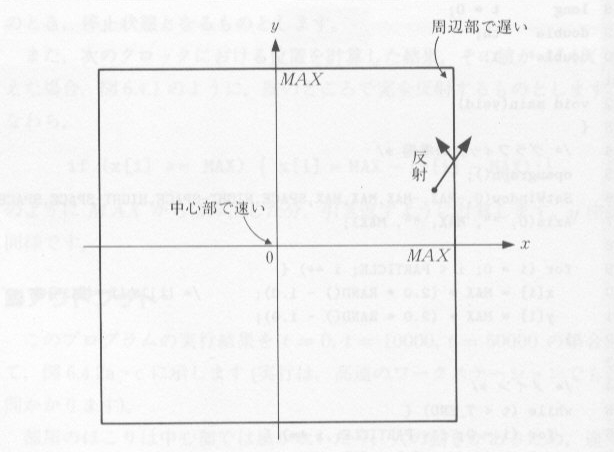 |
| 図6.4.2 ほこりはすみにたまるシミュレーション結果(長時間CPU占有注意) |
 |
| S0640.java ホコリのシミュレーション | Download | 実行(長時間CPU占有注意) | |
/* S0640.java
* ホコリのシミュレーション
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0640 extends Applet implements ActionListener {
Button button0;
Button button1;
int sw =0;
public void init() {
button0 = new Button(" 実行 ");
button1 = new Button("クリア");
add(button0);
add(button1);
button0.addActionListener(this);
button1.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
if (label.equals(" 実行 ")) sw = 1; else sw = 0;
repaint();
}
public void paint(Graphics g) {
Window w ;
w = new Window();
int SPACE = 30;
int HIGHT = 400;
int WIDTH = 640;
int PARTICLE = 1000; /* 粒子の数 */
double MAX = 50.0;
long T_END = 10000;
double x[] = new double[PARTICLE];
double y[] = new double[PARTICLE];
int i; /* 粒子のカウンタ */
long t = 0;
double th;
double l;
/*グラフィックの準備*/
w.setWindow(0, -MAX,-MAX,MAX,MAX, SPACE,HIGHT-SPACE,HIGHT-SPACE,SPACE);
w.axis(0, "", MAX, "", MAX, g);
/*開始*/
if ( sw == 1) {
for (i = 0; i < PARTICLE; i ++) {
x[i] = MAX * (2.0 * Math.random() - 1.0); /* 始めは一様に分布 */
y[i] = MAX * (2.0 * Math.random() - 1.0);
g.setColor(Color.green);
w.putPixel(0, x[i], y[i], g);
}
/*メイン*/
while (t < T_END) {
for (i = 0; i < PARTICLE; i ++) {
g.setColor(Color.white);
w.putPixel(0, x[i], y[i], g);
th = 2.0 * Math.PI * Math.random();
l = (Math.sqrt(2.0) * MAX - Math.sqrt(x[i] * x[i] + y[i] * y[i])) / MAX;
x[i] = x[i] + l * Math.cos(th);
y[i] = y[i] + l * Math.sin(th);
if (x[i] >= MAX) { x[i] = 2*MAX - x[i];} /* 反射 右の壁 */
if (x[i] <= -MAX) { x[i] = -2*MAX - x[i];} /* 反射 左の壁 */
if (y[i] >= MAX) { y[i] = 2*MAX - y[i];} /* 反射 上の壁 */
if (y[i] <= -MAX) { y[i] = -2*MAX - y[i];} /* 反射 下の壁 */
g.setColor(Color.blue);
w.putPixel(0, x[i], y[i], g);
}
w.axis(0, "", MAX, "", MAX ,g);
t = t + 1;
}
stop();
}
}
}
|
| この章始め |
| この章始め |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |