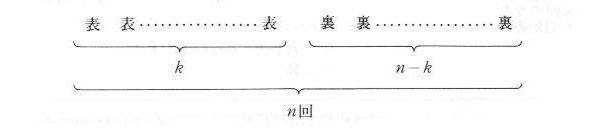
| 図3.1.1 コイン投げ |
 |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |
| 3.1 | コインを投げる実験−−二項分布−− | ||
| 3.2 | ごくまれにしか起こらないこと−−ポアソン分布−− | ||
| 3.3 | ごくまれにしか起こらないことの時間間隔−−指数分布−− | ||
| 3.4 | 大数の法則−−何回も繰り返す−− | ||
| 3.5 | 中心極限定理−−たくさんのサイコロを投げる−− | ||
| 演習 |
| 図3.1.1 コイン投げ |
 |
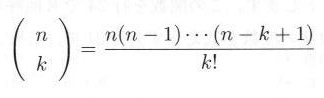 |
・・・・・ | 式3.1.1 |
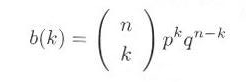 |
・・・・・ | 式3.1.2 |
| 図3.1.2 ベルヌーイ試行 |
 |
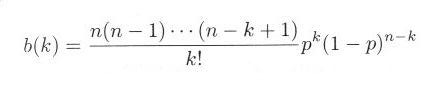 |
・・・・・ | 式3.1.3 |
| 図3.1.3 ベルヌーイの試行の シミュレーション結果 |
 |
| S0310.java ベルヌーイの試行のシミュレーション | Download | 実行 | |
/* S0310.java
* ベルヌーイ試行のシミュレーション
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.*;
public class S0310 extends Applet{
public void paint(Graphics g) {
int M = 1000000; /*発生させる乱数の数*/
int j; /* forのカウンタ */
int k; /* 表の出た回数 */
int n = 6; /* コイン投げの回数 */
int b[] = new int [20]; /* 度数 */
double p = 0.5; /* 表の出る確率 */
double binom; /* 理論値 */
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
for (j = 1; j <= M; j ++) {
k = bernoulli(p, n);
b[k] = b[k] + 1;
}
g.drawString(" k simulation theory", 10, 10);
for (k = 0; k <= n; k ++) {
binom = (double) b[k] / M;
g.drawString(" " + k, 10 , 20 + 10 * k);
g.drawString(" " + exFormat1.format(binom), 40 , 20 + 10 * k);
g.drawString(" " + exFormat1.format(binomial(p, n, k)), 120 , 20 + 10 * k);
}
}
public static int bernoulli(double p, int n){
int k, i;
k = 0;
for (i = 1; i <= n; i++) {
if (p > Math.random()) {
k = k + 1;
}
}
return (k);
}
public static double binomial(double p, int n, int k){
int i;
int k1 = 1;
int n1 = 1;
double b;
for (i = 1; i <= k; i ++) {
k1 = k1 * i;
}
for (i = n - k + 1; i <= n; i++) {
n1 = n1 * i;
}
b = (double)n1 / k1 * Math.pow(p,(double)k) * Math.pow((1 - p), (double)(n - k));
return (b);
}
}
|
| この章始め |
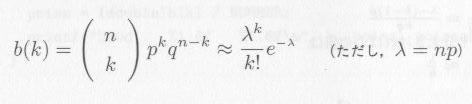 |
・・・・・ | 式3.2.1 |
| 図3.2.1 ポアソン分布の シミュレーション結果 |
 |
| S0320.java ポアソン分布のシミュレーション | Download | 実行 | |
/* S0320.java
* pが小さくnが大きい場合のベルヌーイ試行(ポアソン分布)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.*;
public class S0320 extends Applet{
public void paint(Graphics g) {
int NUMBER = 1000000;
int j; /* forのカウンタ */
int k; /* 成功の回数 */
int n; /* 試行回数 */
int b[] = new int [20]; /* 度数 */
double p; /* 確率 */
double lambda; /* λ */
double poiss; /* ポアソン分布のシミュレーション結果 */
p = 0.01; /* 確率小 */
n = 100; /* 回数大 */
lambda = n * p;
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
for (j = 1; j <= NUMBER; j ++) {
k = bernoulli(p, n);
b[k] = b[k] + 1;
}
g.drawString(" k simulation theory", 10, 10);
for (k = 0; k <= 10; k ++) { /* k=10まで表示 */
poiss = (double)b[k] / NUMBER;
g.drawString(" " + k, 10 , 20 + 10 * k);
g.drawString(" " + exFormat1.format(poiss), 40 , 20 + 10 * k);
g.drawString(" " + exFormat1.format(poisson(lambda, k)), 120 , 20 + 10 * k);
}
}
/* ベルヌーイの試行 */
public static int bernoulli(double p, int n)
{
int k, i;
k = 0;
for (i = 1; i <= n; i++) {
if (p > Math.random()) {
k = k + 1;
}
}
return (k);
}
/* ポアソン分布の理論値 */
public static double poisson(double lambda, int k)
{
int i;
long k1 = 1;
double b;
for (i = 1; i <= k; i ++) { /* kの階乗の計算 */
k1 = k1 * i;
}
b = Math.pow(lambda, (double)k) / (double)k1 * Math.exp(-lambda);
return (b);
}
}
|
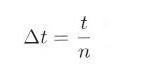 |
・・・・・ | 式3.2.2 |
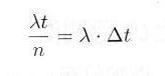 |
・・・・・ | 式3.2.3 |
| 図3.2.1 時系列的な事象発生 |
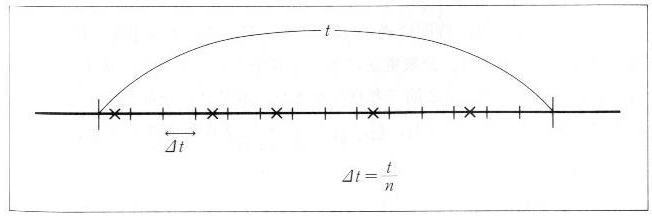 |
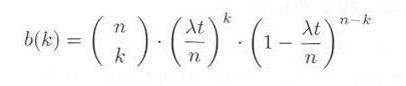 |
・・・・・ | 式3.2.4 |
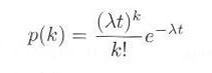 |
・・・・・ | 式3.2.5 |
| この章始め |
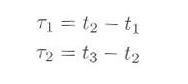 |
・・・・・ | 式3.3.1 |
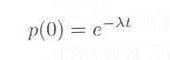 |
・・・・・ | 式3.3.2 |
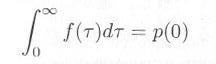 |
・・・・・ | 式3.3.3 |
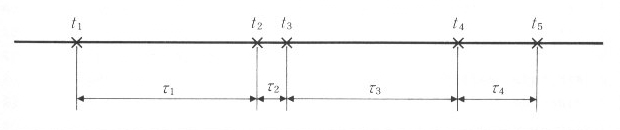
| ・・・・・ | 式3.3.4 |
| 図3.3.1 到着の間隔 |
 |
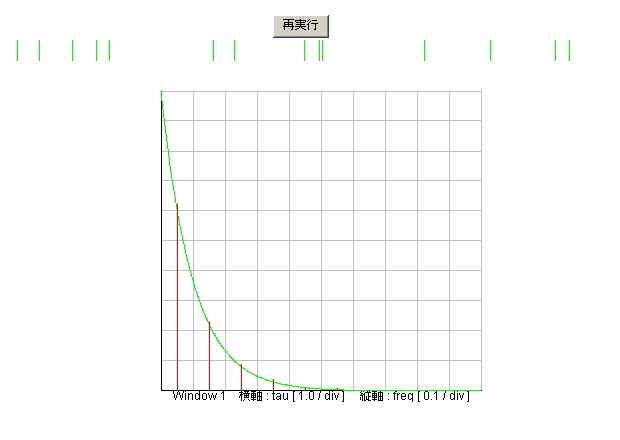
| 図3.3.2 指数分布のシミュレーション結果 |
 |
| S0330.java 指数分布のシミュレーション | Download | 実行 | |
/* S0330.java
* 指数分布のシミュレーション
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0330 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
double T_END = 1000.0; /* シミュレーション終了時刻 */
double T_DISP = 20.0; /* 事象表示時刻 */
int TAU_MAX = 10; /* τの最大値 */
long j; /* 事象発生の回数 */
int f[] = new int[TAU_MAX + 1]; /* ヒストグラム */
int u; /* τの整数部分 */
double lambda = 1; /* λ */
double dt = 0.01; /* 微小時間 */
double t0 = 0.0; /* 一つ前の事象が発生した時刻 */
double t = 0.0; /* 現在の時刻 */
double tau = 0.0; /* 事象発生の間隔τ */
/* グラフィックの準備 */
int SPACE = 20;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0, 0.0, T_DISP, 1.0, 0, (int)(2.5*SPACE), WIDTH, (int)(1.5*SPACE));
w.setWindow(1, 0.0, 0.0, T_DISP/2.0, 1.0,
(int)(0.25*WIDTH), (int)(HIGHT-SPACE), (int)(0.75*WIDTH), (int)(4*SPACE));
w.axis(1, "tau", 1.0, "freq", 0.1, g);
/* メイン */
g.setColor(Color.green);
w.moveTo(1, 0, exponent(lambda, 0), g);
while (tau <= TAU_MAX) {
w.lineTo(1, tau, exponent(lambda, tau),g);
tau = tau + dt;
}
j = 0;
while (t <= T_END) {
if ((lambda * dt) > Math.random()) {
if (t < T_DISP) { w.line(0, t, 0, t, 1,g); }
tau = t - t0;
u = (int)tau;
if (u <= TAU_MAX) { f[u] = f[u] + 1;}
t0 = t;
j = j + 1;
}
t = t + dt;
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < TAU_MAX ; u ++) {
w.line(1, u + 0.5, 0, u + 0.5, (double)f[u] / j,g);
}
}
public double exponent(double lambda, double tau) {
return(lambda * Math.exp(-lambda * tau));
}
}
|
| この章始め |
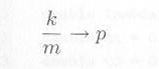 |
・・・・・ | 式3.4.1 |
| 図3.4.1 大数の法則シミュレーション結果 |
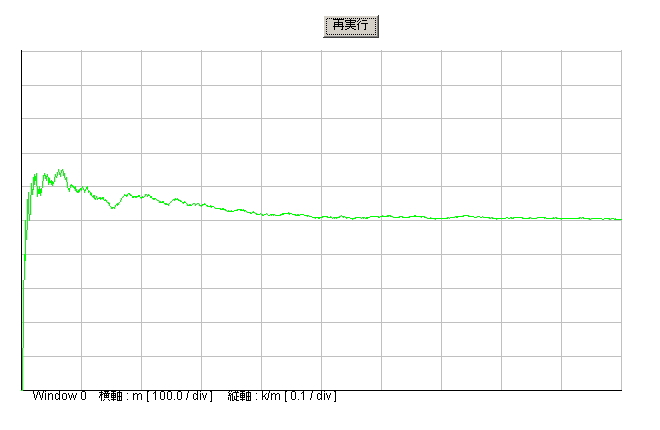 |
| S0340.java 大数の法則シミュレーション | Download | 実行 | |
/* S0340.java
* 大数の法則
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0340 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int SPACE = 20;
int HIGHT = 400;
int WIDTH = 640;
int NUMBER = 1000;
double P = 0.5;
int m;
int k = 0;
w.setWindow(0, 0.0, 0.0, (double)NUMBER, 1.0, SPACE, HIGHT-SPACE, WIDTH-SPACE, 2*SPACE);
w.axis(0, "m", (double)(NUMBER / 10), "k/m", 0.1 , g);
g.setColor(Color.green);
w.moveTo(0, 0.0, 0.0, g);
for (m = 1; m <= NUMBER; m ++) {
if (P > Math.random()) {k = k + 1;}
w.lineTo(0, (double)m, (double)(k) / (double)(m), g);
}
}
}
|
| この章始め |
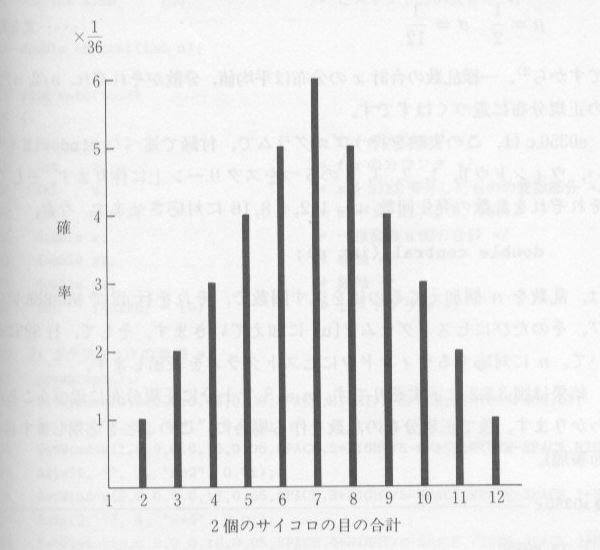
| 図 3.5.1 2個のサイコロ |
 |
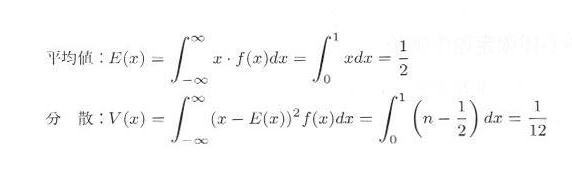 |
・・・・・ | 式3.5.1 |
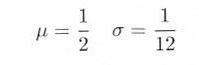 |
・・・・・ | 式3.5.2 |
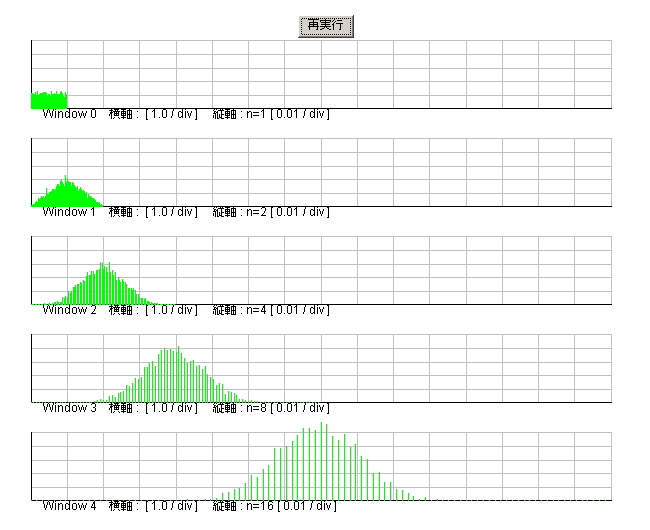
| 図3.5.2 中心極限定理のシミュレーション結果 |
 |
| S0350.java 中心極限定理のシミュレーション | Download | 実行 | |
/* S0350.java
* 中心極限定理
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0350 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g) {
Window w;
w = new Window();
int SPACE = 30;
int HIGHT = 640;
int WIDTH = 640;
int NUMBER = 5000;
double P = 0.5; /* 確率p */
int SIZE = 100; /* ヒストグラムの大きさ */
int j; /* forのカウンタ */
int i; /* forのカウンタ */
int u; /* xをSIZE等分したものの整数部分 */
int n = 1; /* n = 1, 2, 4, 8, 16 */
double x; /* 一様乱数n個の合計 */
double x1; /* 横軸 */
double y1; /* 縦軸 */
int f[] = new int[SIZE]; /* ヒストグラム */
/* グラフィックの準備 */
int hight = HIGHT / 5 - SPACE;
w.setWindow(0, 0.0, 0.0, 16, 0.05, SPACE, hight, WIDTH - SPACE, SPACE);
w.axis(0, "", 1, "n=1", 0.01, g);
w.setWindow(1, 0.0, 0.0, 16, 0.05, SPACE, 2 * hight, WIDTH - SPACE, hight + SPACE);
w.axis(1, "", 1, "n=2", 0.01, g);
w.setWindow(2, 0.0, 0.0, 16, 0.05, SPACE, 3 * hight, WIDTH - SPACE, 2 * hight + SPACE);
w.axis(2, "", 1, "n=4", 0.01, g);
w.setWindow(3, 0.0, 0.0, 16, 0.05, SPACE, 4 * hight, WIDTH - SPACE, 3 * hight + SPACE);
w.axis(3, "", 1, "n=8", 0.01, g);
w.setWindow(4, 0.0, 0.0, 16, 0.05, SPACE, 5 * hight, WIDTH - SPACE, 4 * hight + SPACE);
w.axis(4, "", 1, "n=16", 0.01, g);
g.setColor(Color.green);
/* メイン */
for (i = 0; i < 5; i++) {
for (j = 1; j <= NUMBER; j++) {
x = central(n);
u = (int) (x * SIZE / n);
f[u] = f[u] + 1;
}
/* ヒストグラムを書く */
for (u = 0; u < SIZE; u++) {
x1 = (double)u / SIZE * n;
y1 = (double)f[u] / NUMBER;
w.line(i, x1, 0, x1, y1, g);
f[u] = 0;
}
n = n * 2;
}
}
public double central(int n) {
int k;
double x = 0.0;
for (k = 0; k < n; k++) {
x = x + Math.random();
}
return (x);
}
}
|
| この章始め |
| この章始め |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |