| 図5.1.1 ビュフォンの針 |
 |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |
| 5.1 | モンテカルロ法の古典−−ビュフォンの針−− | ||
| 5.2 | 乱数によりπを求めるもう1つの例−−モンテカルロ法による数値積分−− | ||
| 5.3 | 乱数により球の体積を求める−−モンテカルロ法による多重積分−− | ||
| 演習 |
| 図5.1.1 ビュフォンの針 |
 |
| 図5.1.2 ビュフォンの針 実行結果 |
 |
| S0510.java ビュフォンの針 | Download | 実行 | |
/* S0510.java
* ビュフォンの針
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0510 extends Applet implements ActionListener {
Button button0;
Button button1;
boolean sw = false;
public void init() {
button0 = new Button(" 実行 ");
button1 = new Button("クリア");
add(button0);
add(button1);
button0.addActionListener(this);
button1.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
if (label.equals(" 実行 "))
sw = true;
else
sw = false;
repaint();
}
public void paint(Graphics g) {
Window w;
w = new Window();
int height;
int width;
int NUMBER = 1000; /* 落とした針の本数 */
double MAX = 8.0;
double P = 0.5; /* 確率p */
int j; /* forのカウンタ */
int xl; /* forのカウンタ */
int n1 = 0; /* 針が交わった回数 */
double x0, y0; /* 針の中央の座標 */
double x1, y1, x2, y2; /* 針の先端の座標 */
double th; /* θ */
/* スクリーンの大きさを読み取る */
width = getSize().width;
height = getSize().height;
/* グラフィックの準備 */
w.setWindow(0, 0, 0, MAX, MAX * height / width, 0, height, width - 1, 0);
for (xl = 0; xl <= MAX; xl++) {
w.line(0, xl, 0, xl, MAX, g); /* 平行線 */
}
g.setColor(Color.green); /* 緑 */
/* メイン */
if (sw == true) {
for (j = 1; j <= NUMBER; j++) {
x0 = MAX * Math.random();
y0 = MAX * height / width * Math.random();
th = 2 * Math.PI * Math.random();
x1 = x0 + Math.cos(th) / 2;
y1 = y0 + Math.sin(th) / 2;
x2 = x0 - Math.cos(th) / 2;
y2 = y0 - Math.sin(th) / 2;
w.line(0, x1, y1, x2, y2, g);
if ((int)x1 != (int)x2) { /* (1)針の両端の座標の整数部が異なっている時 */
n1 = n1 + 1;
}
}
g.setColor(Color.black);
g.drawString("pi = " + (double)(j) /(double)(n1) * 2.0, 20, 10);
}
}
}
|
| この章始め |
 |
・・・・・ | 式5.2.1 |
 |
・・・・・ | 式5.5.2 |
| 図5.2.1 1/4円 |
 |
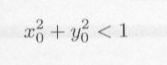 |
・・・・・ | 式5.2.3 |
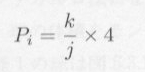 |
・・・・・ | 式5.2.4 |
| 図5.2.2 モンテカルロ法によるπの計算結果 |
 |
| S0520.java モンテカルロ法によるπの計算 | Download | 実行 | |
/* S0520.java
* モンテカルロ法によるπ
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0520 extends Applet implements ActionListener {
Button button0;
Button button1;
boolean sw = false;
public void init() {
button0 = new Button(" 実行 ");
button1 = new Button("クリア");
add(button0);
add(button1);
button0.addActionListener(this);
button1.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
if (label.equals(" 実行 "))
sw = true;
else
sw = false;
repaint();
}
public void paint(Graphics g) {
Window w;
w = new Window();
int height;
int width;
int NUMBER = 10000; /* 雨滴の数 */
int SPACE = 30;
int j; /* forのカウンタ */
int xl; /* forのカウンタ */
int n1 = 0; /* 円の中に入った雨滴 */
double x0, y0; /* 雨滴の座標 */
double pi = 0.0; /* πの近似値 */
/* スクリーンの大きさを読み取る */
width = getSize().width;
height = getSize().height;
/* グラフィックの準備 */
w.setWindow(0, 0, 0, 1, 1, SPACE, height/2 + SPACE, height/2 + SPACE, SPACE);
w.axis(0, "", 1.0,"", 1.0, g);
w.setWindow(1, 0, 0, NUMBER, 4,
SPACE, height - SPACE, width - SPACE, height/2 + 2*SPACE);
w.axis(1, "j", NUMBER / 10, "pi",1.0, g);
/* メイン */
if (sw == true) {
w.moveTo(1, 0.0, 0.0, g);
for (j = 1; j <= NUMBER; j ++) {
x0 = Math.random();
y0 = Math.random();
if (x0 * x0 + y0 * y0 < 1.0) { /* 円の中に入った場合 */
n1 = n1 + 1;
g.setColor(Color.blue);
w.putPixel(0, x0, y0, g);
}
pi = (double)n1 / j * 4;
g.setColor(Color.green);
w.lineTo(1, (double)j, pi, g);
}
g.setColor(Color.black);
g.drawString(" pi = " + pi, 10, 10);
stop();
}
}
}
|
| この章始め |
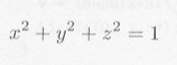 |
・・・・・ | 式5.3.1 |
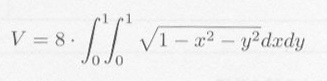 |
・・・・・ | 式5.3.2 |
| 図5.3.1 球 |
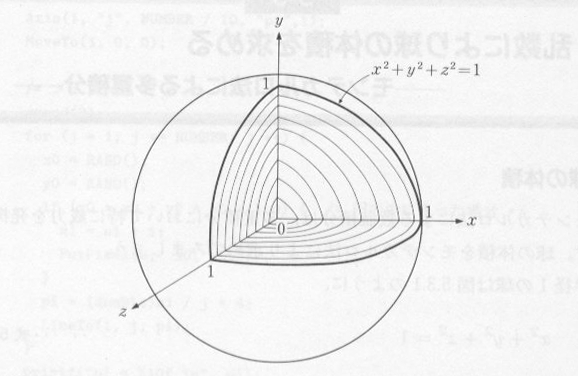 |
| 図5.3.2 モンテカルロ法による球の体積計算結果 |
 |
| S0530.java モンテカルロ法による球の体積計算 | Download | 実行 | |
/* S0530.java
* モンテカルロ法による球の体積計算
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0530 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int SPACE = 20;
int HIGHT = 400;
int WIDTH = 640;
int NUMBER = 1000; /* 乱数の組の数 */
int j; /* forのカウンタ */
int n1 = 0; /* 球の中に入った数 */
double x0, y0, z0; /* 点の座標 */
double v = 0.0; /* 体積の近似値 */
w.setWindow(0, 0, 0, NUMBER, 8, SPACE, HIGHT-SPACE, WIDTH-SPACE, SPACE);
w.axis(0, "j", NUMBER / 10, "v", 1, g);
g.setColor(Color.green);
w.moveTo(0, 0.0, 0.0, g);
for (j = 1; j <= NUMBER; j ++) {
x0 = Math.random();
y0 = Math.random();
z0 = Math.random();
if (x0 * x0 + y0 * y0 + z0 * z0 < 1.0) { /* 球の中に入った場合 */
n1 = n1 + 1;
}
v = (double)n1 / j * 8;
w.lineTo(0, j, v, g);
}
g.setColor(Color.black);
g.drawString(" v = " + v, 10, 10);
stop();
}
}
|
| この章始め |
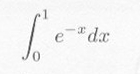 |
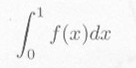 |
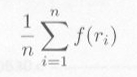 |
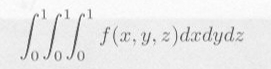 |
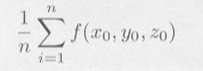 |
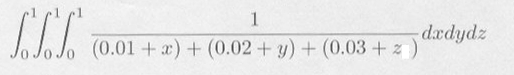 |
| この章始め |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |