| 図2.2.1 S0220.java の実行結果 |
 |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |
| 2.1 | でたらめな数の列--乱数-- | ||
| 2.2 | Javaの乱数発生機構 --Math.random()メソッド-- | ||
| 2.3 | Cの乱数は本当の乱数か--頻度の検定-- | ||
| 2.4 | もう1つの乱数検定方法--ポーカ検定-- | ||
| 演習 |
何の規則性もなしに、物事が起こることをコンピュータで実験するには、でたらめな数の列--乱数--が必要です。この章では、シミュレーションに必ず必要となる、乱数の発生方法と、その性質を理解します。
乱数とは
乱数とは、なんらかの方法で、どの数も等しい確率で、でたらめになるように選んで、数字の列を作ったものです。例えば、さいころをふって出た目を記録すれば、それは1から6までの乱数になります。あるいは、1円のアルミの硬貨を
100枚用意しておき、その1枚、1枚に、00、01、02、・・・、99という番号を書いておき、それを十分かきまぜて、目をつぶって取り出せば、00から99までの乱数となります。
コンピュータによる乱数作り
コンピュータで乱数を発生させるには、いくつかの方法がありますが、例えばある数字(これを“たね”と言います)をなんども掛けあわせると、0から9までの数字がほぼ同数ずつ現われ、規則性も少ないので、乱数発生して使われます。このような方法で作られる乱数は、真の意味の乱数ではなく、疑似乱数と言います。
コンピュータの疑似乱数を乱数として使用する場合は、次のような条件を満足しなければなりません。
① 周期が長いこと
疑似乱数では、まったく同じ数列が繰り返し出現する場合があります。その周期が短いと乱数としての意味がなくなります。
② 統計的検定に耐えること
たとえ、周期が長くとも、
0、 0、 0、 1、 1、 1、 2、 2、 2、 2
といった、ある種の法則に従って出現する数列は、乱数とは言えません。あとで述べる統計的検定という方法で、試験をします。
③ 再現性があること
シミュレーションに用いる場合、同一の乱数を使用して、異なったモデルでシミュレーションし、比較検討する場合があります。またプログラムのデバッグ時にも何度も同じ系列の乱数を必要とする場合があります。すなわち乱数に、再現性が必要されます。
④ 乱数発生のスピードが早いこと
シミュレーションでは、乱数を何度も繰り返し用いて実験を行い、多数回の実験結果から普遍性のある共通因子を求めます。このため乱数発生に要する計算スピードが早くなければなりません。
次に述べるように、Java言語には、Math.random()メソッドという乱数発生機構があり、これは、上記①~④の条件がよく満足されます。
| この章始め |
Math.random()メソッド
JavaのMath クラスのなかにMath.random()メソッドは、あります。(メソッドはC言語の、関数に相当します)
public static double random()
と定義されており、このメソッドが呼び出されるたびに、0.0 以上で、1.0 より小さい正の符号の付いた double 値を返します。戻り値は、この範囲からの一様分布によって擬似乱数的に選択されます。
本ホームページにおいては、このMath.random()メソッドをすべてのプログラムで用いますので、詳しく調べてみることにしましょう。
ためしに簡単なJavaプログラム S0220.java をつくり実行してみます。結果は、20個の小数点以下の乱数が出力されました。
もう一度、このプログラムを実行してみると、別系列の乱数が発生されます。Math.random()メソッドは、実行するたびに初期化され、新しい乱数が作られることに、注意してください。
| 図2.2.1 S0220.java の実行結果 |
 |
| S0220.java Math.randomを使ってみる | Download | 実行 | |
/* S0220.java
* Math.random()を使ってみる
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
public class S0220 extends Applet{
public void paint(Graphics g) {
int NUMBER = 20;
int j;
double r;
for (j = 1; j <= NUMBER; j++){
r = Math.random(); //乱数発生
g.drawString("" + r, 10, j * 10); //rをStringに変換し、draw
}
}
}
|
| この章始め |
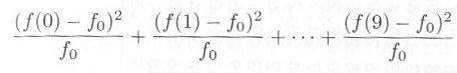 |
・・・・・ | 式2.3.1 |
というものを考えてみます。これを通常 χ2 カイ自乗と読む)と言います。この量は、サンプリング・データと、理論度数とのくい違いの程度を表わしています。もしサンプリング・データと理論度数のくい違いがまったくなければ、χ2 = 0 となり、くい違いが大きいほど χ2 は大きくなります。
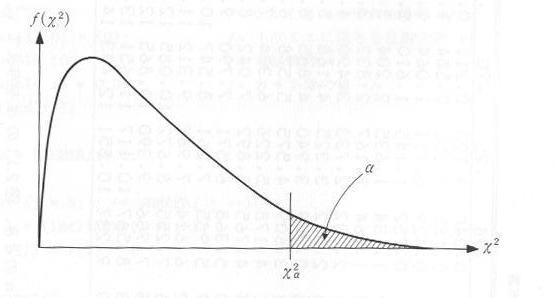
同じ母集団からのサンプリングのやり方は、何通りもあるので、 χ2 は”χ2分布”という分布に従うことが知られています。χ2分布は自由度と呼ばれるパラメータを持っていて、この例では9(キザミの数-1)です。χ2分布は図2.3.1のような形をしており、χ2分布表を表2.3.1に示します。この表は、 χα2 と χα2 の右側の面積αの関係を表わしており、サンプリング・データから得られた χ2 が χα2 より小さければ、”危険率αで理論度数とサンプリング・データが等しい”と言えることになります。
| 図2.3.1 χ2分布 |
 |
頻度検定のプログラム
プログラムS0230.javaでは xs として χ2 を計算しています。このプログラムの実行をクリックして見てください。図2.3.2のように、xs が出力されます。一方、表2.3.1から危険率5%の χα2 は 16.919 ですから、xs はこの値より小さく、したがって5%の危険率で一様分布であると言ってよいことがわかります。すなわち、Math.random()メソッドの頻度テストは合格したことになります。
| 図2.3.2 S0230.javaの実行結果 |
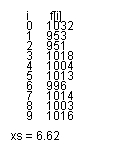 |
| S0230.java 頻度検定 | Download | 実行 | |
/* S0330.java
* 頻度検定
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
public class S0230 extends Applet{
public void paint(Graphics g){
int NUMBER = 10000; /* 発生させる乱数の数 */
int j; /* forのカウンタ */
int i; /* 0.1ごとのキザミの番号 */
int f[] = new int [10]; /* キザミiに落ちる乱数の数 */
double f0; /* 理論度数 */
double xs = 0.0; /* カイ自乗の値 */
f0 = NUMBER/10.0;
for (j = 1; j <= NUMBER; j ++){
i = (int)(Math.random() * 10);
f[i] = f[i] + 1;
}
g.drawString(" i f[i]", 10, 10);
/*頻度の検定*/
for (i = 0; i <= 9; i ++){
g.drawString(" " + i , 10 , 20 + 10 * i);
g.drawString(" " + f[i] , 30 , 20 + 10 * i);
xs = xs + (f[i] - f0) * (f[i] - f0) / f0;
}
g.drawString("xs = " + xs , 10, 30 + 10 * i);
}
}
|
| この章始め |
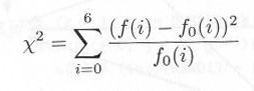 |
・・・・・ | 式2.4.1 |
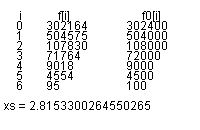
このプログラムの実行してみましょう。図2.4.2が得られます。Math.random()メソッドは、ポーカテストにおいても合格します。
| 図2.4.1 ポーカーテストの方法 |
 |
| 図2.4.2 S0240.java の実行結果 |
 |
| S0240.java ポーカ検定 | Download | 実行 | |
/* S0240.java
* ポーカ検定
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
public class S0240 extends Applet{
public void paint(Graphics g) {
int NUMBER = 1000000; /* 発生させる乱数の数 */
int i; /* 表に示すi */
int count; /* 表に示すcount */
int j, j1, j2, k; /* forのカウンタ */
int f[] = new int[7]; /* iごとの度数 */
int f0[] = new int[7]; /* 理論度数 */
int n[] = new int[5]; /* 5個の数字の並び */
double xs = 0.0; /* カイ自乗値 */
double diff; /* 理論値との差 */
f0[0] = (int)(NUMBER * 0.3024);
f0[1] = (int)(NUMBER * 0.5040);
f0[2] = (int)(NUMBER * 0.1080);
f0[3] = (int)(NUMBER * 0.0720);
f0[4] = (int)(NUMBER * 0.0090);
f0[5] = (int)(NUMBER * 0.0045);
f0[6] = (int)(NUMBER * 0.0001);
for (k = 1; k <= NUMBER; k ++){
for (j = 0; j < 5; j ++){
n[j] = (int)(Math.random() * 10);
}
count = 0;
for (j1 = 0; j1 < 4; j1 ++){
for (j2 = j1 + 1; j2 < 5; j2 ++){
if (n[j1] == n[j2]) {
count = count + 1;
}
}
}
if (count == 10){
i = 6;
} else if (count == 6){
i = 5;
} else{
i = count;
}
f[i] = f[i] + 1;
}
g.drawString(" i f[i] f0[i]", 10, 10);
for (i = 0; i <= 6; i++){
g.drawString(" " + i, 10 , 20 + 10 * i);
g.drawString(" " + f[i], 40 , 20 + 10 * i);
g.drawString(" " + f0[i], 120 , 20 + 10 * i);
diff = f[i] - f0[i];
xs = xs + diff * diff / f0[i];
}
g.drawString(" xs = " + xs, 10, 30 + 10 * i);
}
}
|
| この章始め |
2. 1桁の区間0から9までの乱数があったとき、同じ数が現われるまでの間隔を、ギャップといいます。その長さが r である確率は、
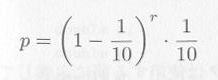 |
| この章始め |
| | HOME | 目次 | | 2009 (C) H.Ishikawa |