 |
|
�W�D�����i�s�̃V�~�����[�V�����Z�@�|�|�@�B�C���̖�����Ɂ|�|
|
�O�̏͂܂łŁA�ł������̊ȒP�ȃV�~�����[�V���������݂܂������A�����̓R�C���𓊂���Ƃ��A�j�𗎂Ƃ��Ƃ��A�����ɂ͂P�̎��ۂ����N����Ȃ��ꍇ
�ł����B�������A��ʂɂ͓����ɕ��s�I�ɁA�������̎��ۂ��i�s����ꍇ����������܂��B���̓����i�s�̃V�~�����[�V�������s�Ȃ��ɂ͂ǂ������炢��
�ł��傤���B���̏͂ł́A�@�B�C���̖��Ƃ����A�����̋@�B������A�����̏C���҂�����Ƃ����A�����i�s�̓T�^�I�Ȃ��̂��Ƃ肠���A�����i�s�̃V�~�����[
�V�����Z�@���}�X�^���邱�ƂƂ��܂��B
�@�B�C�����Ƃ�
�@�������ɁAm ��̐��Y�@�B������Ƃ��܂��B�o�����炷��ƁA���� a ���Ԃ���Ƌ�������Ȃ�̏Ⴕ�܂��B���̏C�������͂P�l�̏C���҂ɂ����
h ���Ԃ�����܂��B���Y�@�B�͂P���Ԃ����� r �~�̎��v�i�����j������A�C���҂͂P�l������P����
c �~�̐l�����������̂Ƃ��܂��B���l�̏C���҂�p�ӂ��C��������ƁA���v�i���v�}�C�i�X��p�j���ő�ƂȂ邩�A���ꂪ�@�B�C���̖��ł�1)�B
�@�̏ᔭ���Ԋu�A�C�����Ԃ��ꂼ�ꂪ�w�����z�̏ꍇ�A���_�I��͂��\�ł���2)�A�����ł͂�����V�~�����[�V�����ɂ���͂��Ă݂܂��傤�B
��
1)�@�X�E�F�[�f���̍H�Ƃʼn��p���ꐬ�����Ă�����̂Ƃ��āA����(1)�ɏЉ����B
2)�@�W�D�S���ɗ��_��͂̃v���O�����������B
�������
�@���̗��̃V�~�����[�V�����͋@�B m ��A�C����n�l���A�Ɨ��ȓ��������܂�����A�����ȒP�ł͂���܂���B�R���s���[�^��p����O�ɁA����������J�[�h��p���Ď��݂ē�������̊T�O�����ނ��ƂƂ��܂��傤�B
�@�@�B�̑䐔 m=5 ��A�C���҂̐l�� n=2 �l�A�̏�̕��ϔ����Ԋu a=10 ���ԁA���ς̏C������ h=4 ���ԂƉ��肵�܂��B
������������́�
�@�̏ᔭ���@�\�F�P�O���̃J�[�h�B���̂����̂P���Ɂu�̏ᔭ���v�Ə����Ă����i�P�O���ԂɂP��̏Ⴗ�邱�Ƃ��A�Ӗ�����j�B
�@�C�������@�\�F�S���̃J�[�h�B���̂����̂P���Ɂu�C�������v�Ə����Ă����i�C�����Ԃ��S���Ԃ��Ӗ�����j�B
�@�@�B�J�[�h�F�T���̃J�[�h�B�@�B�̔ԍ��P�`�T�������Ă����B
�@�L�^�p���F�V�~�����[�V�����̌o�߂��L�^����p���B
������V�~�����[�V������
�@�V�~�����[�V�����̎菇�͎��̂Ƃ���ł��B
�@�@�@�����ݒ�
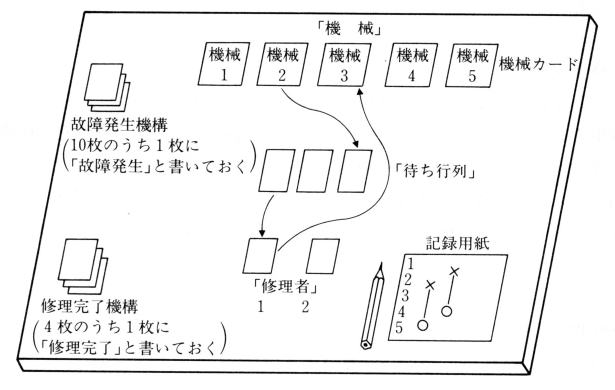
�@�}�W�D�P�D�P�̂悤�Ɋ��̏�́u�@�B�v�̈ʒu�ɋ@�B�J�[�h���T���Ȃ�ׂ�B�܂��u�҂��s��v�̈ʒu�A�u�C���ҁv�̈ʒu���Ă����B�L�^���ɁA�����A�@�B�̏�ԁA�C���҂����Ԃ̋@�B�̕ێ�����Ă��邩���L���ł���悤�ɂ��Ă����B�����͑�P���ԖڂƏ����Ă����B
�@�A �̏ᔭ��
�@�@�B�P�̃J�[�h���u�@�B�v�̈ʒu�ɂ����Ă���A����͉ғ������Ӗ����܂��B�u�̏ᔭ���@�\�v�̃J�[�h���悭�����āA���̂����̂P���������B�u�̏ᔭ
���v�̃J�[�h����������A�@�B�P�̃J�[�h���u�҂��s��v�̈ʒu�ɂȂ�ׂ�B�L�^�p���̂P���Ԗڂ̋@�B�P�̗��Ɂ~�i�̏ᔭ���̃}�[�N�j������B
�@�B�@�̏ᔭ���J�Ԃ�
�@�@�B�Q����T�ɂ��ćA���J��Ԃ��B
�@�C �C���J�n
�@���ɏC���҂P�̈ʒu�ɋ@�B�J�[�h���Ȃ���A���̏C���҂͏C�����łȂ����ғ��̈Ӗ��ł���̂ŁA�u�҂��s��v�̐擪�̋@�B�J�[�h�����o���A�C���҂P�̂Ƃ���ɂ����B�����āA�L�^�p���̏C���҂P�̗��ɁA�C������@�B�ԍ����P�Ə����Ă����B
�@�D �C������
�@�������C���҂P�̈ʒu�ɁA�@�B�J�[�h���u���Ă���A����͏C���҂��C�����ł��邱�ƁA�܂�ғ��������邱�Ƃ��Ӗ����Ă���B�u�C�������@�\�v�̃J�[
�h���悭�����Ă��̒�����P���������B�����u�C�������v�J�[�h����������A���̎��_�ŏC�������ł��邩��A�u�C���ҁv�̈ʒu�ɂ������@�B�J�[�h�����Ƃ�
�u�@�B�v�̈ʒu�ɂ��ǂ��B�L�^�p���̋@�B�̗��Ɂ��i�C�������̃}�[�N�j������B�@
�@�E �C�������J�Ԃ�
�@�C���҂Q�ɂ��ćC�D���J��Ԃ��B
�@�F �ȏ�̎����A�P���Ԃ̒��œ����ɋN�������ł��B���v���P���Ԑi�߁A�A����J��Ԃ��B
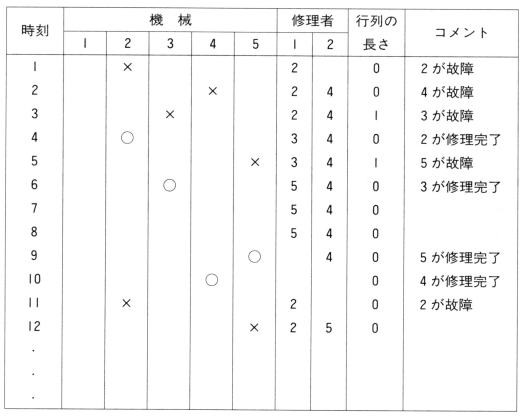
�@�ȏ�ɂ��A���\���ԕ����J��Ԃ��A�L�^�p��������A�\�W�D�P�D�P�̂悤�ɂȂ�ł��傤�B�e�@�B�������Ԍ̏�ł��������A�C���J�n�܂ʼn����ԑ҂�����邩�A�C���҂͂ǂ̂��炢�ғ����Ă������A���̕\����v�Z���邱�Ƃ��ł���ł��傤�B
�@���̕��@�́A�R�D�P�߂ŏq�ׂ��x���k�[�C���s�̎����̉��p�ŁA���v���ꎞ��߂āA���ׂĂ̋@�B�A�C���҂ɑ��A�x���k�[�C���s���s������A���v��i�߂�ƍl���ĉ������B���ꂪ�����i�s�̃V�~�����[�V�������@�ł��B
| �}�W�D�P�D�P ������� |
 |
| �\�W�D�P�D�P�@�L�^�p�� |
 |
�R���s���[�^�ŋ@�B�C����������
�@�W�D�P�߂̊�������ŁA�����i�s���ۂ̃V�~�����[�V�����̊T�O�͂��߂��Ǝv���܂����A��������S���ԕ��������Ȃ��ƁA�M���̂�����@�B�̉ғ����A�C��
�҂̉ғ����Ȃǂ͋��߂��܂���B�܂��A�����̐i�ߕ����A�P���Ԃ�P�ʂɂ��Ă��܂����A�R�D�R�߂ŏq�ׂ��悤�ɏ\���ɔ����Ȏ��ԂƂ��āA���̒��ɂQ�̎�
�ۂ̋N����Ȃ��悤�ɂ��Ȃ���Ȃ�܂���B���̂悤�ȖړI�̂��߂ɂ́A�R���s���[�^�̎�������̂��ǂ��ł��傤�B�����ŁA���������R���s���[�^�ŃV
�~�����[�V�������邱�Ƃɂ��܂��傤�B
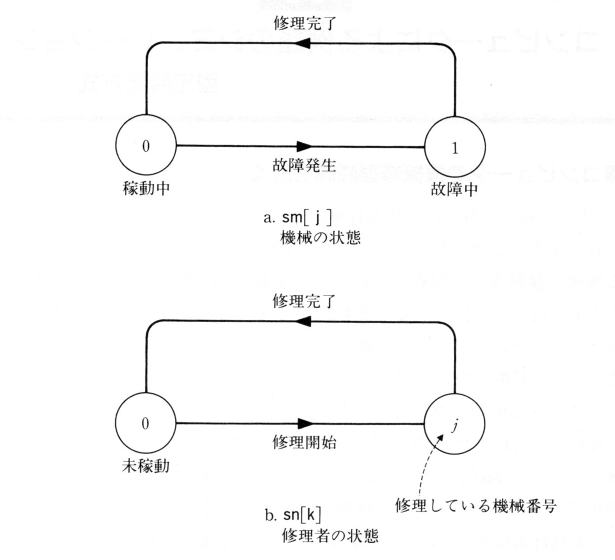
�@�v���O����S0820.java�ł́A���̕ϐ���p���܂��B��������ŁA���̏�ɒu���Ă����u�@�B�v�J�[�h�́A sm[j] �ɑ������A���̒l���O�ł���A�ғ����A�P�ł���Ό̏ᒆ�ł��邱�Ƃ������܂��B�C���҂̏�Ԃ�
sn[k] �ŕ\�킵�܂��B���̒l���A�O�ł���Ζ��ғ��i�Ђ܂ȏ�ԁj�A�P�`�T�ł���@�B�P����@�B�T���C�����Ă��邱�Ƃ������܂��B���̗l�q��}�W�D�Q�D�P�Ɏ����܂��B���̂悤�Ȑ}����ԑJ�ڐ}�ƌ����܂��B�܂��A
q �͑҂��s��̒������A sq[q] �͑҂��s��� q �ԖڂɂȂ��ł���@�B�̔ԍ���\�킷���ƂƂ��܂��B
| �}�W�D�Q�D�P �@�B�C�����̏�ԑJ�ڐ} |
 |
�v���O�����̃|�C���g
�@�v���O����S0820.java���A�@�B�C���̖����V�~�����[�V��������v���O�����ł��B�W�D�P�߂̊�������ƑΔ䂷��ƁA(1)���A�A�A�B�ɑΉ����܂��B(2)���u�̏ᔭ���@�\�v�ɑ������܂��B(3)�ő҂��s��ɂ��܂��B(4)���W�D�P�߂̇C�A�D�A�E�ɑ������܂��B(5)���C�̏C���J�n�ł��B
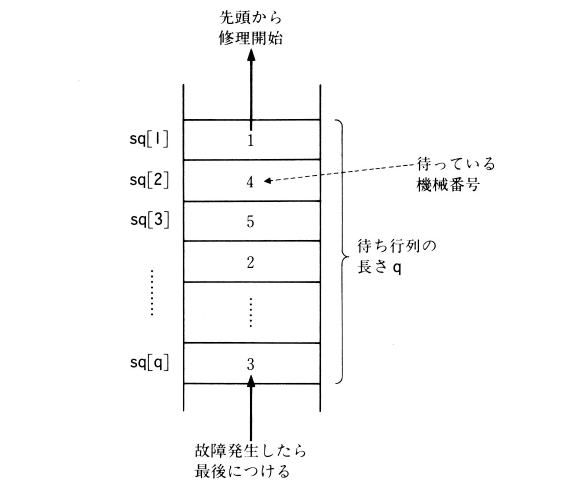
�@�҂��s�� sq[q] �͐}�W�D�Q�D�Q�̂悤�ȍ\���ƂȂ��Ă���Aq �̒l���҂��s��̍Ō���������Ă��܂�����A q+1 �ɋ@�B�ԍ������邱�Ƃ́A�҂��s��ɐV���ɂȂ�Ԃ��Ƃ��Ӗ����A sq[1] ���Ƃ�o���Α҂��s��̐擪���Ƃ�o���܂��B(6)�ɂ����āA�s�P�����O�i�ނ��Ƃ������Ă��܂��B(7)�́u�C�������@�\�v�������Ă��܂��B(8)�ȍ~�͋L�^�p���ւ̋L���ɑ������A(9)�͎����� DT �����i�߂܂��B
| �}�W�D�Q�D�Q �҂��s��̍\�� |
 |
���s
���s����ƁAm=5, n=2, a=10, h=4�̏ꍇ�A�}�W�D�Q�D�R�̌��ʂ������ADT=0.5�Ƃ��Ă��܂�����A�O�D�T���Ԃ��̋L�^���Ƃ��A�\�W�D�P�D�P�ƑΔ䂷�邱�Ƃ��ł��܂��B
�}�W�D�Q�D�R�@�Œ莞�ԕ����V�~�����[�V��������
(�����j |
 |
| S0820.java�@�@�B�C���̖�� (�Œ莞�ԕ���) �@| Download | ���s | |
/* S0820.java
* �@�B�C���̖�� (�Œ莞�ԕ���)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.DecimalFormat;
public class S0820 extends Applet{
int M = 5; /* �@�B�̑䐔 */
int N = 2; /* �C���҂̐l�� */
double A = 10.0; /* ���ό̏ᔭ���Ԋu */
double H = 4.0; /* ���ϏC������ */
double DT = 0.5; /* �������� */
double T_END = 30.0; /* �V�~�����[�V�������I�鎞�� */
public void paint(Graphics g) {
double tt = 0.0; /* �V�~�����[�V�����N���b�N */
int i; /* �҂��s���for�̃J�E���^ */
int j; /* �@�B��for�̃J�E���^ */
int k; /* �C���҂�for�̃J�E���^ */
int f = 0; /* �̏Ⴕ�Ă���@�B�̑䐔 */
int q = 0; /* �҂��s��̒��� */
int l = 0;
int sm[] = new int[M + 1]; /* �@�Bj�̏�� */
int sn[] = new int[N + 1]; /* �C����k�̏�� */
int sq[] = new int[M + 1]; /* �҂��s�� */
double p[] = new double[M + 1]; /* �@�B��f��̏Ⴕ�Ă��鎞�Ԃ̊��� */
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
g.drawString
(" tt sm[j] sn[k] sq[i]",
10, 10);
/* �J�n */
while (tt <= T_END) {
/* (1)�̏ᔭ�� */
for (j = 1; j <= M; j ++) {
if (sm[j] == 0) { /* �@�B���ғ����Ȃ� */
if ((1.0 / A * DT) > Math.random()) { //(2)
sm[j] = 1; /* ����m���Ō̏Ⴗ�� */
q = q + 1; /* (3)�҂��s��̌��ɂ� */
sq[q] = j;
}
}
}
/* (4)�̏�C�� */
for (k = 1; k <= N; k ++) {
if (sn[k] == 0) { /* (5)�C���҂����ғ��Ȃ� */
if (q > 0) {
sn[k] = sq[1]; /* �҂��s����o�� */
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i ++) {
sq[i] = sq[i + 1];
/* (6)�҂��s���1�i�߂� */
}
}
}
} else {
if ((1.0 / H * DT) > Math.random()) {
/* (7)�C���҂͋@�B���C���� */
sm[sn[k]] = 0;
/* �ғ���Ԃɂ��� */
sn[k] = 0;
}
}
}
/* (8)�\�� */
g.drawString(" " + tt, 10, 20 + 10 * l);
for (j = 1; j <= M; j ++) g.drawString(" " + sm[j],
50 + 10 * j, 20 + 10 * l );
for (k = 1; k <= N; k ++) g.drawString(" " + sn[k],
100 + 10 * M +10 * k, 20 + 10 * l );
for (i = 1; i <= q; i ++) g.drawString(" " + sq[i],
150+ 10 * (M + N) + 10 * i, 20 + 10 * l );
l= l + 1;
/* �̏Ⴕ�Ă���@�B�̑䐔�𐔂��� */
f = 0;
for (j = 1; j <= M; j ++) {
if (sm[j] == 1) { f = f + 1; }
}
p[f] = p[f] + DT;
/* (9)������i�߂� */
tt =tt + DT;
}
/* ���ʏo�� */
for (j = 0; j <= M; j ++) {
g.drawString("p["+ j + "]="+ " "
+ exFormat1.format((double)p[j] / T_END) ,
10 , 20 + 10 * l + 10 * j);
}
}
}
|
�ʂȕ��@�ŋ@�B�C����������
�@�W�D�Q�߂̃v���O�����́A�ȕւł����A���̓_�ɓ����܂��B����́A����
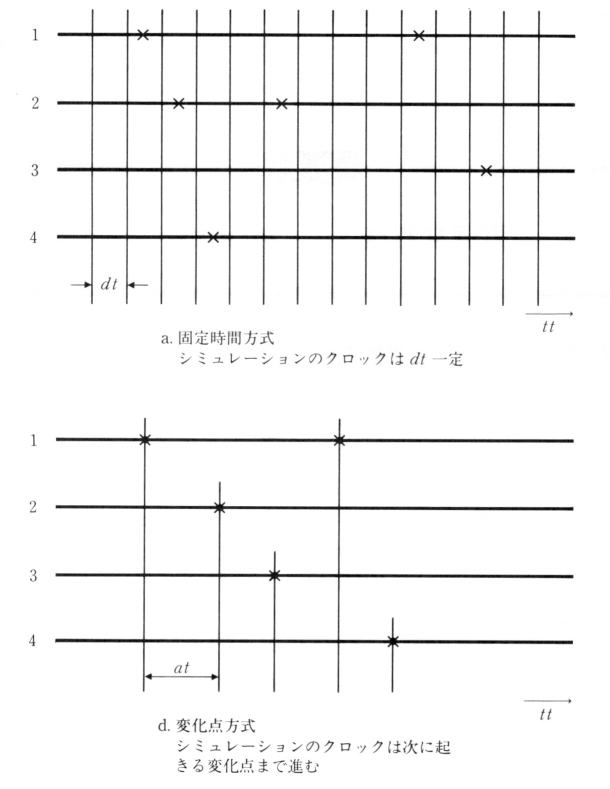
tt �̐i�ߕ��ɂ��Ăł��Btt �́A�L�U�~ DT �ό̏�Ԋu a ���邢�͕��ϏC������ h �ɔ䂵�\������������K�v������܂��B�R�D�Q�߂ŏq�ׂ��Ƃ���Adt ���傫���Ƃ������Ƃ́A���鎞�ԓ��ɔ������鎖�ۂ͂Q�����z�ƂȂ邱�Ƃ��Ӗ����A�����_���ȃ|�A�\�����z�Ƃ͈قȂ��Ă��܂��܂��B
�@����ł� DT ������������Ƃ���A���̕ω����Ȃ����i�̏�����������A�C���������Ȃ����j�ɂ��A�v�Z�����Ȃ���Ȃ炸�A�V�~�����[�V�������Ԃ������Ȃ�܂��B
�@����ɔ�ׁA�����ŏq�ׂ�ω��_�����́A�}�W�D�R�D�P���̂悤�ɕω����N����܂ł̎��Ԃ��v�Z���āA���̊Ԃ̎������X�L�b�v��������ŁA���炩�̏�ԕ�
��������Ƃ������A��ԕω��̃v���O�����������悤�ɂ��܂��B���̂��߂ɂ́A���݂��炠�Ɖ��b�i�����j��Ɏ��̏�Ԃ��ω����邩�Ƃ����A���Ԃɑ������闐
����p���܂��B����ɂ͂S�͂ŏq�ׂ����@���p�����܂��B�Ⴆ�A��̗��ŁA����@�B���C�������ƂȂ����Ƃ��A���Ɍ̏Ⴗ��܂ł̎��Ԃ͎w�����z�ƂȂ�
�܂�����A�v���O����S0420.java�ō�����w�����z������p���A���Ɍ̏Ⴗ��܂ł̎��Ԃ��v�Z���܂��B
�@�����_�������̎w�����z�݂̂Ȃ炸�A�S���ŏq�ׂ��e��̕��z������p����A���܂��܂Ȏ��ԊԊu���V�~�����[�V�����ł��邱�Ƃ��A���̕����̓����ł��B
| �}�W�D�R�D�P�@�Œ莞�ԕ����ƕω��_���� |
 |
�v���O�����̃|�C���g
�@���ăv���O����S0830.java�ɂ��A�ω��_�����̃V�~�����[�V�����̐��������܂��B�v���O����S0820.java�ɔ�ׁA�v���O��������Ⓑ���Ȃ��Ă��܂��Bsm[j], sn[k], q, sq[q] �͂W�D�Q�߂̏ꍇ�Ɠ����ł��B(1)�����̕ϐ��ɉ����āAtm[j], tn[k] �Ƃ����ϐ������炽�ɓ������܂��Btm[j] �́A�@�Bj�� sm[j] �̏�Ԃɂ��Ɖ����ԂƂǂ܂��Ă��邩�A���̎c�莞�Ԃ�\�킵�܂��B�Ⴆ�Asm[1]=0 �ŁAtm[1]=3.68 �ł���A�u�@�B�P�����݉ғ����ŁA����3.68���Ԍ�Ɍ̏Ⴊ��������v���Ƃ��Ӗ����܂��B�܂�
sn[2]=3 �� tn[2]=1.20 �ł���A�u�C����2�́A���@�B�R��ێ炵�Ă���A���ƂP�D�Q�O���Ԍ�ɏC����������v���Ƃ��Ӗ����܂��B����
tm[j] ���邢�� tn[k] �ɂ����āA�@�B�̏C�������������A���邢�͕ێ�҂��C�����J�n���邽�тɎw�������������A���ɋN����ω��_�܂ł̎��Ԃ��Z�b�g���邱�ƂƂ��܂��B
�@���Ɏ���tt�̐i�ߕ��Ɋւ��ẮA���ׂĂ̋@�B�� tm[j] �A���邢�́A���ׂĂ̕ێ�҂� tn[k] �̒�����ł��������l�i���ꂪ�ł��߂��N���鎖�ۂł��j��T���A���̒l���O�ɂȂ�܂Ői�߂܂��B
�@(2)�ŋ@�B 1 ���� M ���u�ғ����v�ɁA�C���� 1 ���� N �܂ł��u���ғ��v�ɏ����ݒ肵�܂��B�����ŏC���҂̑҂����Ԃ���ɐݒ肵�܂��B�@(3)���炪���C���E�v���O�����ŁA�@�B1����M�ɑ���Ԃ̕ω��������܂��B(4)�� tm[j] ���O�̋@�B�A���Ȃ킿�̏Ⴕ���@�B������(5)�� sm[j]=1 �ɕω������A�҂��s��ɂȂ�ׂ܂��B�����ŁA tm[j] �̒l�͕��������_�ł�����A���x�����Z���J��Ԃ��Ă���ԂɁA���S�ɂO�łȂ����Ƃ��z�肳��܂��̂ŁA tm[j] �̐�Βl�� EPS �Ƃ����\���������l��菬�����ꍇ���O�Ƃ݂Ȃ��Ă��܂��B
�@(6)���C���҂̓������L�q���Ă��܂��B(7)�� tn[k]=0 �̏C�����I�����C���҂�T���A(8)�ł��̏C�����Ă����@�B���ғ���Ԃɂ��܂��B(9)����
k �̏C���҂����������C���������������A�ȑO���疢�ғ��̏ꍇ�͑҂��s��ׂ܂��B�҂��s��ɋ@�B������A(10)���̒��ɂȂ��ł���@�B�����o���ĕێ炵�܂��B
�@(11)�ŁA tm[j], tn[k] �̒��ŁA�ł��������l��T���A�����at�Ƃ��܂��B���̒l���A���̌n�̒��ŁA���ɂ������ԕω��܂ł̎��ԂƂȂ�܂��B(12)�ȉ��ŁA���ׂĂ�
tm[j], tn[k] ���� at �������A�܂��N���b�N tt �� at �����i�߂܂��B
�@(13)�ȉ����r���o�߂��L�^���镔���A(14)�ȉ����̏Ⴕ�Ă���@�B�̑䐔�𐔂��镔���ł��B
���s����
�@���s����ƁAm=5, n=2, a=10, h=4 �̏ꍇ�A�}�W�D�R�D�Q�̌��ʂ������܂��B�����͕s�A���I�ɐi�s���Ă���A�P�s�o�͂��邽�тɋ@�B���A�C���҂̏�Ԃ��ω����Ă���̂��킩��܂��B
| �}�W�D�R�D�Q�@�ω��_�����V�~�����[�V�������� |
 |
| S0830.java�@�@�B�C���̖�� (�ω��_����) �@| Download | ���s | |
/* S0830.java
* �@�B�C���̖�� (�ω��_����)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.DecimalFormat;
public class S0830 extends Applet{
int M = 5; /* �@�B�̑䐔 */
int N = 2; /* �C���҂̐l�� */
double A = 10.0; /* ���ό̏ᔭ���Ԋu */
double H = 4.0; /* ���ϏC������ */
double DT = 0.5; /* �������� */
double T_END = 100.0; /* �V�~�����[�V�������I�鎞�� */
double INF = 1.0e100; /* �\���傫���l */
double EPS = 1.0e-100; /* �\���������l */
public void paint(Graphics g) {
double tt = 0.0; /* �V�~�����[�V�����N���b�N */
int i; /* �҂��s���for�̃J�E���^ */
int j; /* �@�B��for�̃J�E���^ */
int k; /* �C���҂�for�̃J�E���^ */
int f = 0; /* �̏Ⴕ�Ă���@�B�̑䐔 */
int q = 0; /* �҂��s��̒��� */
int l = 0; /* �\���s */
int sm[] = new int[M + 1]; /* �@�Bj�̏�� */
double tm[] = new double[M + 1];
/* (1)�@�B�Ɏ��̏�ԕω����N��܂ł̎��� */
int sn[] = new int[N + 1]; /* �C����k�̏�� */
double tn[] = new double[N + 1];
/* (1)�C���҂Ɏ��̏�ԕω����N��܂ł̎��� */
int sq[] = new int[M + 1]; /* �҂��s�� */
double p[] = new double[M + 1];
/* (1)�@�B��f��̏Ⴕ�Ă��鎞�Ԃ̊��� */
double at; /* �������� */
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
DecimalFormat exFormat2 = new DecimalFormat(" 0.00");
g.drawString
(" tt sm[j] sn[k] sq[i]",
10, 10);
/* (2)�����ݒ� */
for (j = 1; j <= M; j ++) {
sm[j] = 0; tm[j] = -A * Math.log(1 - Math.random())
}
for (k = 1; k <= N; k ++) {
sn[k] = 0; tn[k] = INF;
}
/* (3)�J�n */
while (tt <= T_END) {
/* �̏ᔭ�� */
for (j = 1; j <= M; j ++) {
if (Math.abs(tm[j]) < EPS) { /* (4)�@�Bj���̏ᔭ�� */
sm[j] = 1; tm[j] = INF; /* (5) */
q = q + 1;
sq[q] = j;
}
}
/* (6)�̏�C�� */
for (k = 1; k <= N; k ++) {
if (Math.abs(tn[k]) < EPS) {
/* (7)�C����k�̏C�������� */
sm[sn[k]] = 0;
tm[sn[k]] = -A * Math.log(1 - Math.random());
/* (8) */
}
if (Math.abs(tn[k]) <EPS || sn[k] == 0) {
/* (9)k�����ғ��̏ꍇ */
if (q > 0) { /* (10)�҂��s������o�� */
sn[k] = sq[1];
tn[k] = -H * Math.log(1 - Math.random());
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i ++) {
sq[i] = sq[i + 1];
}
}
} else {
/* �҂��s��Ȃ�C����k�͖��ғ���ԂɂȂ� */
sn[k] = 0; tn[k] = INF;
}
}
}
/* (13)�\�� */
g.drawString(" " + exFormat2.format(tt), 10, 20 + 10 * l);
for (j = 1; j <= M; j ++) {
g.drawString(" " + sm[j],
50 + 10 * j, 20 + 10 * l );}
for (k = 1; k <= N; k ++) {
g.drawString(" " + sn[k],
100 + 10 * M +10 * k, 20 + 10 * l );}
for (i = 1; i <= q; i ++) {
g.drawString(" " + sq[i],
150+ 10 * (M + N) + 10 * i, 20 + 10 * l );}
l= l + 1;
/* (11)���ɏ�ԕω��̋N�鎞�������߂� */
at = INF;
for (j = 1; j <= M; j ++) {
if (tm[j] < at) at = tm[j];
}
for (k = 1; k <= N; k++) {
if (tn[k] < at) at = tn[k];
}
/* (14)�̏Ⴕ�Ă���@�B�̑䐔�𐔂��� */
f = 0;
for (j = 1; j <= M; j ++) {
if (sm[j] == 1) { f ++; }
}
p[f] = p[f] + at;
/* (12)���Ԃ�i�߂� */
for (j = 1; j <= M; j ++) {
tm[j] = tm[j] - at;
}
for (k = 1; k <= N; k ++) {
tn[k] = tn[k] - at;
}
tt = tt+ at;
}
/* ���ʏo�� */
for (j = 0; j <= M; j ++) {
g.drawString("p["+ j + "]="+ " "
+ exFormat1.format((double)p[j] / T_END)
,10 , 20 + 10 * l + 10 * j);
}
}
}
|
�Œ莞�ԕ����ƕω��_����
�@���������Q�̕����i�Œ莞�ԕ����ƕω��_�����j�ŃV�~�����[�V���������݂܂����B�����̔�r���������Ǝv���܂��B��r���ڂ͌v�Z�@���ԂƁA���_�l�ɑ���덷�ł��B T_END=10000 ���ԕ��̃V�~�����[�V�������Œ莞�ԕ����ɂ��Ă�dt=1 ���ԁA0.1 ���ԁA0.01 ���ԂƂ��Ď��s���A�ω��_�����Ɣ�r���邱�ƂƂ��܂��B
���_�l
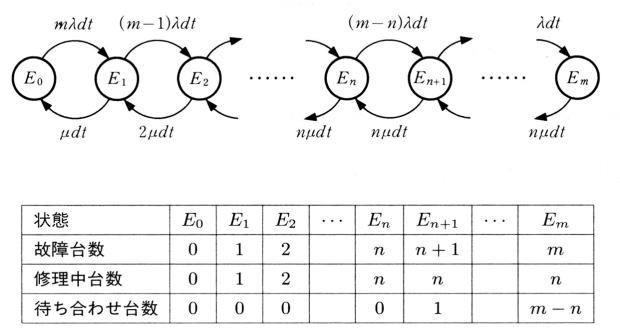
�@���_�l�͌̏ᔭ���Ԋu�A�C�����ԂƂ��w�����z�̏ꍇ�A���̂悤�ɋ��߂邱�Ƃ��ł��܂��B�@�B��j �䂱���Ă����Ԃ�Ej
�Ə����ƁA��ԑJ�ڐ}�́A�}�W�D�S�D�P�̂悤�ɏ������Ƃ��ł��܂��B�����Ń� �͒P�ʎ��Ԃ�����̌̏�m���A��
�͒P�ʎ��Ԃ�����̏C�������m���ŁA��=1/a�A��=1/h
�ł��B���̐}�ō�����E�ֈڍs����Ƃ������Ƃ́A�@�B�������̏Ⴗ��Ƃ������ƂŁA���̑J�ڂ͌̏Ⴕ�Ă��Ȃ��@�B�̑䐔�ɔ�Ⴕ�Ă�����܂��B�]��
�āAdt �Ƃ����������Ԃ̊Ԃ�(m-j)��dt
�Ƃ����m���őJ�ڂ��邱�ƂɂȂ�܂��B�E���獶�ւ̑J�ڂ́A�̏Ⴕ�Ă����@�B���A�C��������Ă����Ƃ����Ӗ��ŁA���̊����́Aj ��n
���傫���ꍇ�́An��dt �Ƃ����m���ŁAj ��n ��菬�����ꍇ�́A���ݏC�����̑䐔�ɔ�Ⴕ��j��dt �Ƃ����m���ŏC���������܂��B
�@���鎞��t ��Ej �Ƃ�����Ԃɂ���m����pj(t) �Ə����A���̐}����A�������Ԍo�ߌ��pj(t+dt) �����̂悤�ɁA����킷���Ƃ��ł��܂��B
| �}�W�D�S�D�P |
 |
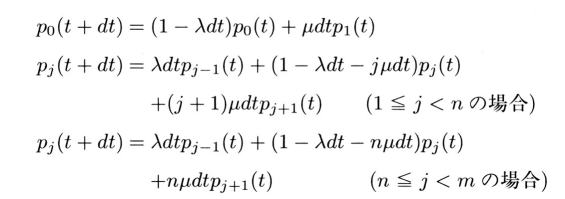 |
�E�E�E |
���W�D�S�D�P |
�����ŁA����Ԃ̉������߂邽�߁A
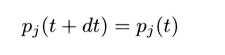 |
�E�E�E�E�E |
���W�D�S�D�Q�� |
�Ƃ��A��������߂�pj�Ə����ƁA�����̎��W�D�S�D�P��
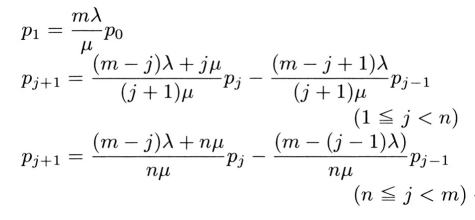 |
�E�E�E |
���W�D�S�D�R |
�܂��B����炩��Ap0 ����p1 ,p1 ����p2 ,p3 ����p4 �Ƃ����悤�ɋ��߂Ă����ƁA
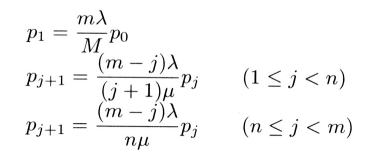 |
�E�E�E |
���W�D�S�D�S |
�������A(p1 + p2 + p3 +�E�E�E+ pm = 1)
�Ƃ����Q�����邱�Ƃ��ł��܂��B
�@���̎�����v���O����S0840.java���������Ƃ��ł��܂��B���̃v���O�����ł�pj �� p[j] �Am �� M �An �� N �A1/�� �� A �A1/�� �� H �ƕ\�킵�Ă��܂��B
�������̔�r
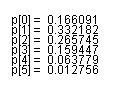
�@�O�߂Ŏg�������l���S0840.java�ɂ��A���_�l���v�Z���A�Œ莞�ԕ����ƕω��_�����̔�r�������Ȃ��܂��B�}�W�D�S�D�Q������
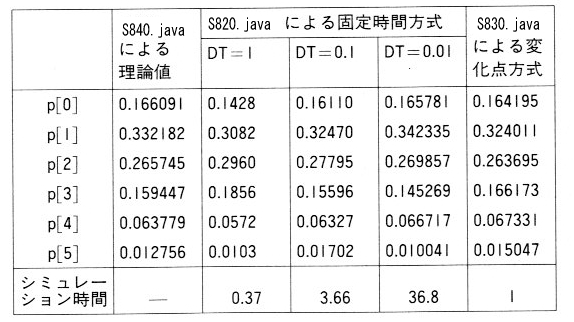
��܂��B��r�\��\�W�D�S�D�P�Ɏ����܂��B�ω��_�����͎��s���x�����������A���x���ǂ����Ƃ��킩��܂��B�܂��Œ莞�ԕ����́A���Ƃŏq�ׂ�A�ɊǗ���
��̂悤�ɂP���P�ʂɋN����ω����V�~�����[�V��������ꍇ�Ȃǂɂ́A�v���O�������P���ƂȂ�܂�����A�ǂ��p�����܂��B���ɂ���Ďg��������̂���
�낵���B
�}�W�D�S�D�Q�@S0840.java��
���� |
 |
| �\�W�D�S�D�P �Œ莞�ԕ����ƕω��_�����̔�r |
 |
| S0840.java�@�@�B�C���̖�� (���_�l) �@| Download | ���s | |
/* S0840.java
* �@�B�C���̖�� (���_�l)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.DecimalFormat;
public class S0840 extends Applet{
int M = 5; /* �@�B�̑䐔 */
int N = 2; /* �C���҂̐l�� */
double A = 10.0; /* ���ό̏ᔭ���Ԋu */
double H = 4.0; /* ���ϏC������ */
public void paint(Graphics g) {
int j; /* �@�B��for�̃J�E���^ */
double p[] = new double[M + 1];/* �@�B��f��̏Ⴕ�Ă��鎞�Ԃ̊��� */
double p0 = 0.0;
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
p[0] = 1;
p[1] = (double)M * H / A * p[0];
for (j = 1; j <= N - 1; j ++) {
p[j + 1] = (double)(M - j) / (j + 1) * H / A * p[j];
}
for (j = N; j <= M - 1; j ++) {
p[j + 1] = (double)(M - j) / N * H / A * p[j];
}
for (j = 0; j<= M; j ++) {
p0 = p0 + p[j];
}
for (j = 0; j<= M; j ++) {
p[j] = p[j] / p0;
}
for (j = 0; j <= M; j ++) {
g.drawString("p["+ j + "] ="+ " " + exFormat1.format(p[j] )
,10 , 20 + 10 * j);
}
}
}
|
�@�V�~�����[�V�����������Ȃ��ꍇ�C�M���ɑ��錋�ʂ�̂ɂǂ̂��炢�v�Z�@���̂��K�v�ł��傤���BJAVA�A�v���b�g���g���A�ŏI���ʂ�
�A�E�g�v�b�g����݂̂Ȃ炸�C�r���̌o�߂��f�B�X�v���C���邱�Ƃ��ł��܂�����C���̌`���݂āC�������C���肷�邱�Ƃ��ł��܂��B
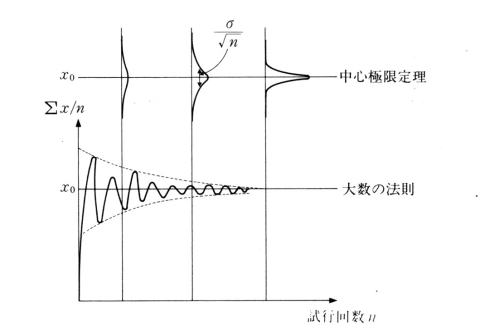
�@�f�B�X�v���C�̉�ʂɂ́C�����Ɏ��s���邢�̓V�~�����[�V�����N���b�N�C�c���Ɍ��ʂ��Ƃ�ƁC�}�W�D�T�D�P�̂悤�ȃO���t���\�������ł��傤�B��
�Ȃ킿�C�n�߂͂�����傫���C�������ɁC��������čs���܂��B�R�D�S�߂̑吔�̖@���ƁC�R�D�T�߂̒��S�Ɍ��藝���C�v�������ĉ������B�c���͂��鎎�s
�̌��ʁC�����̉Ǝ��s�̉̔�ł�����C�吔�̖@���ɂ��C���s��
n
�𑽂�����ƈ��l�ɋ߂Â��킯�ł��B������C���̏ꍇ�̃o���c�L�͂ǂ��ł��傤���B���S�Ɍ��藝�́C�@x�@�̕��z�ɂ�����炸�C�@x�@���@n�@���v
���C�@n�@�Ŋ���ƁC�W�������C�@�P�^��n�@�̐��K���z�ƂȂ�Ƃ����Ă��܂��B�@n�@��傫������ƕW�����͏��������S�ɋ߂����킯�ł��B�������C��
�̊����́@n�@���C�P�O�O�{���Ă��C�W�����́C�P�^�P�O�ɂ����Ȃ�܂���B�܂�C�P�����x���グ�悤�Ƃ���C�V�~�����[�V�������Ԃ��P�O�O�{������
�K�v������܂��B
| �}�W�D�T�D�P�@�V�~�����[�V�������Ԃƌ��ʂ̎��� |
 |
�P�D�@�@�B�̑䐔���T��A�̏�̕��ϔ����Ԋu���P�O���ԁA���ϏC�����ԁ��S���ԁA�P���Ԃ�����̋@�B�P��̎��v���W���~�A�C���҂P�l�P���Ԃ�����̔�p���Q���~�Ƃ����Ƃ��A�ő嗘�v�������闝�_�I�ȏC���҂̐l�������߂Ȃ����B
�@�@�i�j�@�@A0810.java �@| ���s |
�@�@�@�@�@�@�@�@����ɂ��A�Q�l���ŗ�
�Q�D�@�v���O����S0830.java�ŁA�C�����Ԃ��ʑ�k=3�̃A�[�������z�Ƃ����ꍇ�ɂ��āA�V�~�����[�V�������Ȃ����B
�@�@�i�j�@�@A0820.java �@| ���s |
�R�D�@�v���O����S0830.java���������āA�̏Ⴕ�Ă���@�B�̊��� pf[j]/tt ���A���X���X�\�����A�V�~�����[�V�����̎������A�ϑ��ł���悤�ɂ��Ȃ����B�܂��@�B�̉ғ����A�C���҂̉ғ����A�@�B�̑҂����Ԃ̕��z�A�@�B�̑҂����킹���ώ��ԁA���̕��U�����߂�悤�ɂ��Ȃ����B
�@�@�i�j�@�@A0830.java �@| ���s |
�S�D�@�P�{�̓��͐��� m �l�̗n�ڍH�����p���Ă��܂��B�n�ڍH�̓����_���ɒf���I�ɂP�`�̓d�����g�p���܂��B���̎��Ԃ̕��ϒl�� h ���ŊԊu�̕��ς� a ���ł��B�d���̔g�`���V�~�����[�V�������Ȃ����B
�@�@�i�j�@�@A0840.java �@| ���s |
|
 |
