 |
前章で、シミュレーションの基本となる乱数発生の準備ができました。本章では、確率論としてよく知られているいくつかの理論を、実際に乱数を使って実験
をして、確かめることにします。単に数式として理解していたつもりのことが、確率実験をすることによって具体性が増し、理解が深まることでしょう。
本章以後では、計算結果をグラフ表示しますので、スクリーン座標と論理座標を変換するclass、Window.javaを使用します。
ベルヌーイ試行
コイン投げのように繰り返し行う試行で、表が出るか裏がでるかというように、ただ2つの結果だけが可能で、それらの起こる確率が各試みを通じて一定であるなら、これをベルヌーイの試行といいます。
この表が出るか、裏が出るか2つの確率を p と q で表わしたとき(ただし p + q = 1 ), n 回のベルヌーイ試行を行ったとしましょう。
| 図3.1.1 コイン投げ |
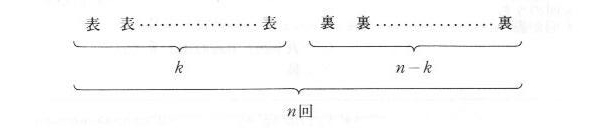 |
たまたま、図3.1.1 という順序で結果が現われたとすると、それが起こる確率は
pk・qn-k です。このほかの順序で、表が k 回、裏が n - k 回起こる確率も同様に pk・qn-k です。これらの確率の和が、 n 回の試行中に k 回の表と n - k 回の裏が出る確率となります。そのような系列の数は、 n 個の物から一度に k 個の物をとり出す方法に等しいので、
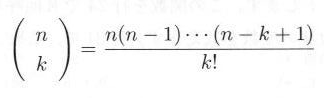 |
・・・・・ |
式3.1.1 |
となることが知られています。(この数を2項係数と言う。)したがって、 n 回のベルヌーイの試行を行って、成功の数(表の出た回数)だけが関心時で、その順序は問題にしないとき、
k 回の成功と n - k 回の失敗が起こる確率は、
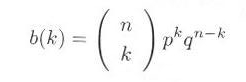 |
・・・・・ |
式3.1.2 |
であらわされます。これを二項分布と言います。
二項分布のシミュレーション
p = 0.5 、すなわちコイン投げの例をコンピュータでシミュレーションしてみましょう。図3.1.2
のとおり、コインを n 回ずつくぎって、 m 回、計 n×m 回投げることとします。
| 図3.1.2 ベルヌーイ試行 |
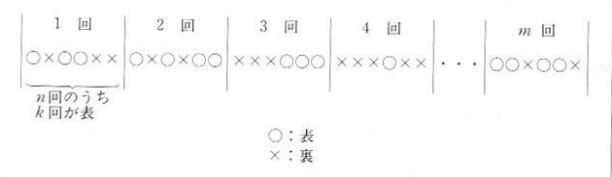 |
n 回のうち k 回成功(表が出る)と考えます。プログラムS0310.javaでは、この n 回のコイン投げを
int bernoulli(double p, int n);
というメソッドで表現しています。つまり、このメソッドは、成功した回数を値として返します。このメソッドの中にある
p > Math.random() は、 Math.random() の値が p より小さい時、表が出たことを意味することとして、k をカウントします。このメソッドを、M 回呼び、 b[k] として成功した回数 k の度数を数えます。これを M で割り、二項分布を求めます。
二項分布の理論値
次に理論値を計算します。先の式3.1.2は
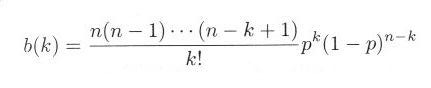 |
・・・・・ |
式3.1.3 |
となりますから、プログラムS0310.javaのメソッド
double binomial(double p, int n , int k);
でこの式を計算します。n1 で (n-1)・・・(n-k+1) を計算して、k1 でk! を計算しています。
下のS0310.javaを実行してみましょう。図3.1.3のようにシミュレーションと理論値はよく一致しています。たしかにコイン投げの結果は二項分布になることがわかります。
図3.1.3 ベルヌーイの試行の
シミュレーション結果 |
 |
| S0310.java ベルヌーイの試行のシミュレーション | Download | 実行 | |
/* S0310.java
* ベルヌーイ試行のシミュレーション
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.*;
public class S0310 extends Applet{
public void paint(Graphics g) {
int M = 1000000; /*発生させる乱数の数*/
int j; /* forのカウンタ */
int k; /* 表の出た回数 */
int n = 6; /* コイン投げの回数 */
int b[] = new int [20]; /* 度数 */
double p = 0.5; /* 表の出る確率 */
double binom; /* 理論値 */
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
for (j = 1; j <= M; j ++) {
k = bernoulli(p, n);
b[k] = b[k] + 1;
}
g.drawString(" k simulation theory", 10, 10);
for (k = 0; k <= n; k ++) {
binom = (double) b[k] / M;
g.drawString(" " + k, 10 , 20 + 10 * k);
g.drawString(" " + exFormat1.format(binom), 40 , 20 + 10 * k);
g.drawString(" " + exFormat1.format(binomial(p, n, k)),
120 , 20 + 10 * k);
}
}
public static int bernoulli(double p, int n){
int k, i;
k = 0;
for (i = 1; i <= n; i++) {
if (p > Math.random()) {
k = k + 1;
}
}
return (k);
}
public static double binomial(double p, int n, int k){
int i;
int k1 = 1;
int n1 = 1;
double b;
for (i = 1; i <= k; i ++) {
k1 = k1 * i;
}
for (i = n - k + 1; i <= n; i++) {
n1 = n1 * i;
}
b = (double)n1 / k1 * Math.pow(p,(double)k)
* Math.pow((1 - p), (double)(n - k));
return (b);
}
}
|
ポアソン分布とは
コイン投げの場合、表の出る確率は、 p=0.5 という比較的大きな値でした。ここではベルヌーイ試行のうち p が小さい、ごくまれにしか起こらな
い場合を考えてみましょう。例えば、1ページあたりのミスプリントの数、一日あたりの交通事故の件数、パンに入っている乾ぶどうの数などです。ミスプリン
トの場合を例にとりますと、1文字を印刷するときの誤りの確率 p はたいへん低く、1ページ分の全文字すなわち n 回のベルヌーイ試行を行なったと考
えられます。 ベルヌーイ試行において、 p が小さく n が大きいとき、式3.1.2は次のように変形されます(注)。
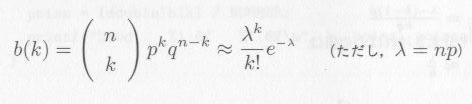 |
・・・・・ |
式3.2.1 |
これをポアソン分布と言い、以下これを p(k) と書くこととします。
ポアソン分布のシミュレーション
先のベルヌーイの試行実験のプログラムを改造して、 p を小さく n を大きくして実行してみなしょう。例えば、 p=1/100 、 n=100 とした場合を、プログラムS0320.javaに示します。
ポアソン分布の理論値
次に式3.2.1によりポアソン分布の理論値を計算します。プログラムS0320.javaのメソッド
double poisson(double lambda, int k);
が式3.2.1の計算です。 λ をこのプログラムでは lambda で表現しています。 λ=100×1/100=1 として実行した
結果が得られます。 図3.2.1のように
n を大きく p を小さくしたベルヌーイ試行は、理論値とよく一致しており、ごくまれにしか起こらないベルヌーイ試行は、ポアソン分布で近似できること
が、シミュレーション実験で理解できるでしょう。
図3.2.1 ポアソン分布の
シミュレーション結果 |
 |
| S0320.java ポアソン分布のシミュレーション | Download | 実行 | |
/* S0320.java
* pが小さくnが大きい場合のベルヌーイ試行(ポアソン分布)
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.text.*;
public class S0320 extends Applet{
public void paint(Graphics g) {
int NUMBER = 1000000;
int j; /* forのカウンタ */
int k; /* 成功の回数 */
int n; /* 試行回数 */
int b[] = new int [20]; /* 度数 */
double p; /* 確率 */
double lambda; /* λ */
double poiss; /* ポアソン分布のシミュレーション結果 */
p = 0.01; /* 確率小 */
n = 100; /* 回数大 */
lambda = n * p;
DecimalFormat exFormat1 = new DecimalFormat(" 0.000000");
for (j = 1; j <= NUMBER; j ++) {
k = bernoulli(p, n);
b[k] = b[k] + 1;
}
g.drawString(" k simulation theory", 10, 10);
for (k = 0; k <= 10; k ++) { /* k=10まで表示 */
poiss = (double)b[k] / NUMBER;
g.drawString(" " + k, 10 , 20 + 10 * k);
g.drawString(" "
+ exFormat1.format(poiss), 40 , 20 + 10 * k);
g.drawString(" "
+ exFormat1.format(poisson(lambda, k)), 120 , 20 + 10 * k);
}
}
/* ベルヌーイの試行 */
public static int bernoulli(double p, int n)
{
int k, i;
k = 0;
for (i = 1; i <= n; i++) {
if (p > Math.random()) {
k = k + 1;
}
}
return (k);
}
/* ポアソン分布の理論値 */
public static double poisson(double lambda, int k)
{
int i;
long k1 = 1;
double b;
for (i = 1; i <= k; i ++) { /* kの階乗の計算 */
k1 = k1 * i;
}
b = Math.pow(lambda, (double)k) / (double)k1 * Math.exp(-lambda);
return (b);
}
}
|
時系列的にランダムに起きること
放射性物質の崩壊や、9章に述べる電話交換機に入ってくる通話の呼、駅の自動販売機に到着する客のように、時間の経過のうちに起こってくる、ランダムな事象の確率分布は、ポアソン分布となります。このような到着のし方をポアソン到着といいます。
ポアソン到着は、待ち行列理論、トラヒック理論などの基本となり、重要ですので、もう少し詳しく考えてみましょう。単位時間あたりに発生する事象の平均数を λ で表わせば、任意の長さの時間間隔 t 内に発生する事象の平均数は λt です。
次に t を n 個の小区間 Δt ずつに分けると(図3.2.1参照)
 |
・・・・・ |
式3.2.2 |
ですが、区間数 n を十分大きくとり、したがって Δt を十分小さくすると、 Δt の間に事象が2回発生する確率が無視できるようになります。特定の小区間 Δt において、事象の発生する確率を求めれば、
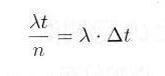 |
・・・・・ |
式3.2.3 |
となります。
| 図3.2.1 時系列的な事象発生 |
 |
これは時間経過が Δt あるごとに、 p=λt/n の確率のベルヌーイ試行を行っていると見ることができます。したがって、前節の式3.1.2にこの p を代入すれば、
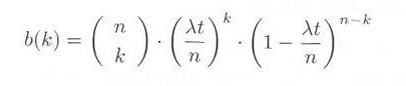 |
・・・・・ |
式3.2.4 |
となりますが、 λΔt《1 ですので、二項分布のポアソン近似式3.2.1により、
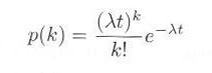 |
・・・・・ |
式3.2.5 |
となります。
これが、単位時間にあたりλ の到着のある事象において、時間間隔 t に、ちょうど k 単位の到着がある確率を表わします。
例えば、平均1分間に1人ずつランダムに公衆電話をかけに客がやってくるとき、 λt=1 ですから、1分間に0人、1人、2人、3人、・・・到着する確率は、S0320.javaの実行結果のとおり、 0.36788, 0.36788, 0.18394, 0.06131,・・・ となるわけです。
ポアソン分布と指数分布は表と裏の関係
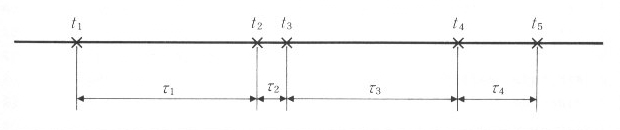
次に考察するのは、時間経過のうちにランダムに生起する事象の、時間の間隔の分布です。例えば、公衆電話に次々と客がやってきたとします。時間 t 内に到着する客の数は3.2節で考察したとおり、ポアソン分布となります。では、図3.3.1のようにt1、t2、t3、・・・と客が到着するとき、
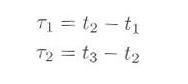 |
・・・・・ |
式3.3.1 |
のような「到着の間隔」は、どのような確率になるでしょうか。
ポアソン分布の3.2節の式3.2.5において、 k=0 、すなわち 0 から t までの間に客が到着しなかったとすると、
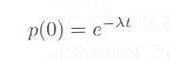 |
・・・・・ |
式3.3.2 |
となり、この値は相次いで起こる事象の間隔が t よりも大きい確率に相当します。一方、間隔の確率を f(τ) と書くと、 0 から t までの間に到着しなかった確率は、
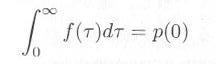 |
・・・・・ |
式3.3.3 |
となり、式3.3.2と式3.3.3を f(τ) について解くと、
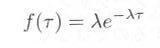 |
・・・・・ |
式3.3.4 |
が得られます。この式は”ポアソン到着の場合の間隔は指数分布にしたがう”ということを、表わしています。
| 図3.3.1 到着の間隔 |
 |
指数分布のシミュレーション
コンピュータで乱数を発生させ、事象の起こる時間間隔が本当に指数分布になるかどうか実験し、実感としてつかんでみることにします。それがプログラムS0330.javaです。
このプログラムでは、計算結果をグラフ表示しますので、スクリーン座標と論理座標を変換するclass、Window.javaを使用します。
時刻は t で表わされ、 dt という微小時間ずつ進めます。単位時間に事象の起こる平均確率 λ を lambda と、また τ を tau と表現しています。 dt 内に事象は lanbda * dt の確率で、たかだか1つ起こります。それを(1)で乱数を発生させ表現しています。すなわち
dt ごとに 1/100 の発生確率の事象をおこさせているわけです。(2)で1つ前に起こった時刻との差 τ を求め、(3)で τ の整数部分の頻度をカウントします。
理論値はどうなるでしょうか。式3.3.4を関数
double exponent(double lambda, double tau);
のとおり、計算します。
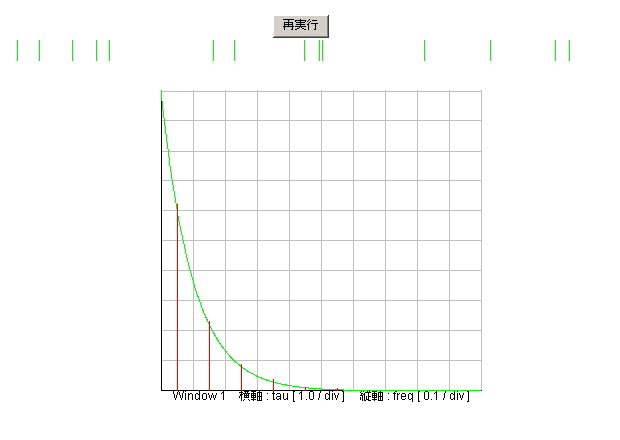
プログラムS0330.javaを実行すると、図3.3.2のように、まずウインドウ1に理論値が緑で表示された後、画面の上部に事象発生の都度、たて線が表示されます。たて線の間隔は、細かく接近しているところも、間があいているところもあります。この間隔の分布を
t が T_END になるまで計測し、ウインドウ1にヒストグラムとして棒グラフに表示します。理論値とよく一致し、たしかに、ごくまれにおこる事象の時間間隔は指数分布となっていることが確かめられました。
時系列的にごく希にしか起らないとされている、航空機事故、地震などが、時として頻発することがあります。このシミュレーションでも示されたように、こ
のようなことは、けっして等間隔に発生するのではなく、ある時は接近して、またあるときは、はなれて「忘れた頃に」発生することに注意しましょう。
| 図3.3.2 指数分布のシミュレーション結果 |
 |
| S0330.java 指数分布のシミュレーション | Download | 実行 | |
/* S0330.java
* 指数分布のシミュレーション
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0330 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
double T_END = 1000.0; /* シミュレーション終了時刻 */
double T_DISP = 20.0; /* 事象表示時刻 */
int TAU_MAX = 10; /* τの最大値 */
long j; /* 事象発生の回数 */
int f[] = new int[TAU_MAX + 1]; /* ヒストグラム */
int u; /* τの整数部分 */
double lambda = 1; /* λ */
double dt = 0.01; /* 微小時間 */
double t0 = 0.0; /* 一つ前の事象が発生した時刻 */
double t = 0.0; /* 現在の時刻 */
double tau = 0.0; /* 事象発生の間隔τ */
/* グラフィックの準備 */
int SPACE = 20;
int HIGHT = 400;
int WIDTH = 640;
w.setWindow(0, 0.0, 0.0, T_DISP, 1.0, 0,
(int)(2.5*SPACE), WIDTH, (int)(1.5*SPACE));
w.setWindow(1, 0.0, 0.0, T_DISP/2.0, 1.0,
(int)(0.25*WIDTH), (int)(HIGHT-SPACE),
(int)(0.75*WIDTH), (int)(4*SPACE));
w.axis(1, "tau", 1.0, "freq", 0.1, g);
/* メイン */
g.setColor(Color.green);
w.moveTo(1, 0, exponent(lambda, 0), g);
while (tau <= TAU_MAX) {
w.lineTo(1, tau, exponent(lambda, tau),g);
tau = tau + dt;
}
j = 0;
while (t <= T_END) {
if ((lambda * dt) > Math.random()) {
if (t < T_DISP) { w.line(0, t, 0, t, 1,g); }
tau = t - t0;
u = (int)tau;
if (u <= TAU_MAX) { f[u] = f[u] + 1;}
t0 = t;
j = j + 1;
}
t = t + dt;
}
/* ヒストグラムを書く */
g.setColor(Color.red);
for (u = 0; u < TAU_MAX ; u ++) {
w.line(1, u + 0.5, 0, u + 0.5, (double)f[u] / j,g);
}
}
public double exponent(double lambda, double tau) {
return(lambda * Math.exp(-lambda * tau));
}
}
|
大数の法則
一般に確率 p のある事象(コイン投げの例では表の出ること)に関して、試行を
m 回行ったとき、その事象の起こる回数が k 回であるとすれば、比率 k/m は試行回数が大きくなるにつれて一定の値に近づくでしょう。これを大数の法則と言います。すなわち、
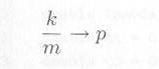 |
・・・・・ |
式3.4.1 |
となるはずです。
大数の法則の実験
コイン投げの例では、表の出る確率は 1/2 に近づくことが期待できます。実際にシミュレーションで大数の法則を実験してみましょう。
プログラムS0340.javaは1000回コインを投げ、そのたびに k/m の値をプロットするプログラムです。実行をクリックして実験してみて下さい。
図3.4.1のように k/m=0.5 に収束していくのがわかります。
| 図3.4.1 大数の法則シミュレーション結果 |
 |
| S0340.java 大数の法則シミュレーション | Download | 実行 | |
/* S0340.java
* 大数の法則
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0340 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g){
Window w ;
w = new Window();
int SPACE = 20;
int HIGHT = 400;
int WIDTH = 640;
int NUMBER = 1000;
double P = 0.5;
int m;
int k = 0;
w.setWindow(0, 0.0, 0.0,
(double)NUMBER, 1.0, SPACE, HIGHT-SPACE, WIDTH-SPACE, 2*SPACE);
w.axis(0, "m", (double)(NUMBER / 10), "k/m", 0.1 , g);
g.setColor(Color.green);
w.moveTo(0, 0.0, 0.0, g);
for (m = 1; m <= NUMBER; m ++) {
if (P > Math.random()) {k = k + 1;}
w.lineTo(0, (double)m, (double)(k) / (double)(m), g);
}
}
}
|
マージャンのサイコロ
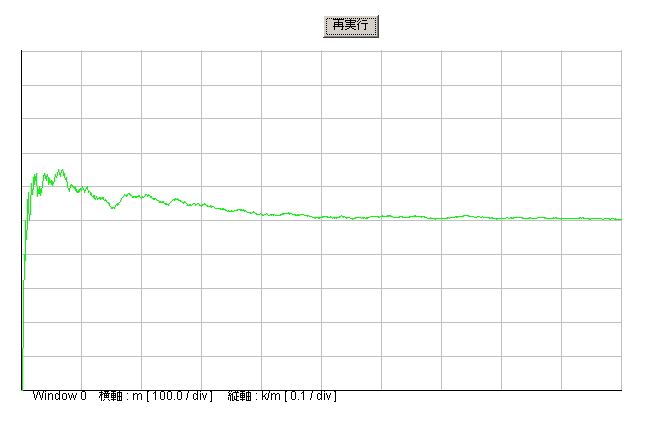
マージャンの親を決める時のサイコロのふり方は、2個同時に投げ、その合計で決めます。皆さんご存知のとおり、図3.5.1のように2個のサイコロの目
の合計は、2から12までに分布しますが、7の場合の確率が最も高いのです(この場合三角分布となります。)一度にふるサイコロの数が多くなったとき、ど
うなるでしょうか。
| 図 3.5.1 2個のサイコロ |
 |
中心極限定理とは
同一の分布に従う n 個の乱数があったとします。その合計 x の分布はどうなるかを考えます。もとの分布の平均値を μ 、分散を σ2 とすると、もとの分布が何であろうと、 n の値(先の例ではサイコロの数)が大きくなるにつれて、平均が nμ 、分散が nσ2 の正規分布に近づくのです。これを中心極限定理と言います。
中心極限定理の実験
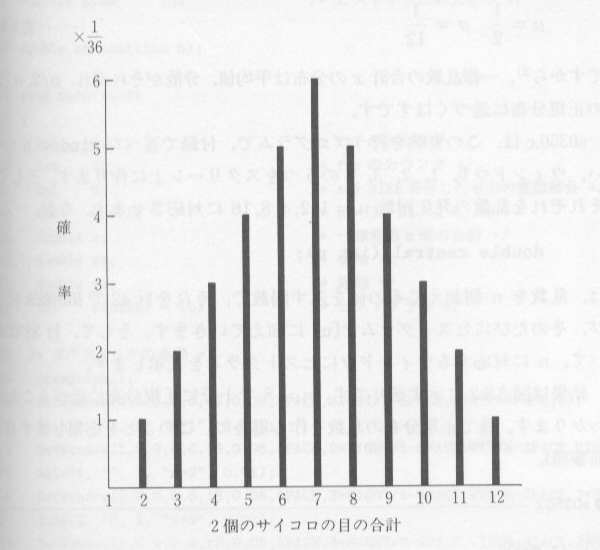
このことを乱数実験によりたしかめましょう。いま、 区間 [0,1) の一様乱数を
n 個発生させたとします。一様乱数の平均値 μ 、分散 σ2 は
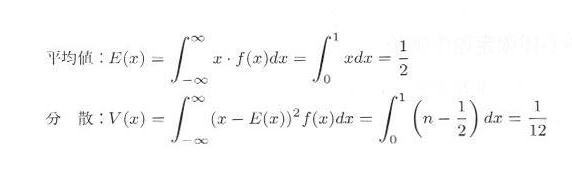 |
・・ |
式3.5.1 |
となり
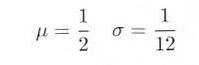 |
・・・・・ |
式3.5.2 |
ですから、一様乱数のn個の合計 x の分布は平均値、分散がそれぞれ、 n/2、n/12 の正規分布に近づくはずです。
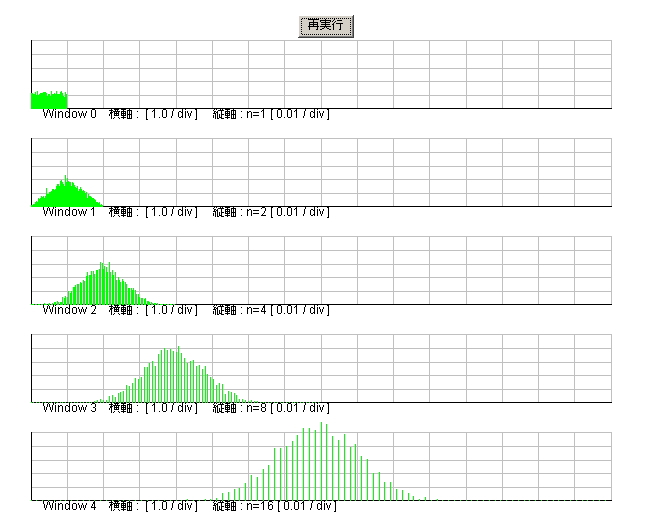
プログラムS0350.javaは、この実験を行うプログラムで、(1)スクリーン座標と論理座標を変換するclass、Window.javaを使用し、ウインドウ0、1、2、3、4の5つをスクリーン上に作ります。それぞれ乱数の発生回数
n = 1, 2, 4, 8, 16 に対応させます。 (2)の
double central (int n);
は、乱数を n 個加えてその値を返すメソッドで、それを(3)で NUMBER 回よび、そのたびにヒストグラム f[u] に加えていきます。そして、(4)において、 n に対応するウインドウにヒストグラムを表示します。
実行をクリックすると図3.5.2のように結果が表示されるでしょう。 n = 8 で十分に正規分布に近づくことがわかります。あとで、正規分布の乱数を作る場合にこのことを応用することとします。(4.5節参照)
| 図3.5.2 中心極限定理のシミュレーション結果 |
 |
| S0350.java 中心極限定理のシミュレーション | Download | 実行 | |
/* S0350.java
* 中心極限定理
* (C) H.Ishikawa 2008
*/
package simulation;
import java.applet.*;
import java.awt.*;
import java.awt.event.*;
import window.Window;
public class S0350 extends Applet implements ActionListener {
Button button0;
public void init() {
button0 = new Button(" 再実行 ");
add(button0);
button0.addActionListener(this);
}
public void actionPerformed(ActionEvent e) {
String label = e.getActionCommand();
repaint();
}
public void paint(Graphics g) {
Window w;
w = new Window();
int SPACE = 30;
int HIGHT = 640;
int WIDTH = 640;
int NUMBER = 5000;
double P = 0.5; /* 確率p */
int SIZE = 100; /* ヒストグラムの大きさ */
int j; /* forのカウンタ */
int i; /* forのカウンタ */
int u; /* xをSIZE等分したものの整数部分 */
int n = 1; /* n = 1, 2, 4, 8, 16 */
double x; /* 一様乱数n個の合計 */
double x1; /* 横軸 */
double y1; /* 縦軸 */
int f[] = new int[SIZE]; /* ヒストグラム */
/* グラフィックの準備 */
int hight = HIGHT / 5 - SPACE;
w.setWindow(0, 0.0, 0.0, 16, 0.05,
SPACE, hight, WIDTH - SPACE, SPACE);
w.axis(0, "", 1, "n=1", 0.01, g);
w.setWindow(1, 0.0, 0.0, 16, 0.05,
SPACE, 2 * hight, WIDTH - SPACE, hight + SPACE);
w.axis(1, "", 1, "n=2", 0.01, g);
w.setWindow(2, 0.0, 0.0, 16, 0.05,
SPACE, 3 * hight, WIDTH - SPACE, 2 * hight + SPACE);
w.axis(2, "", 1, "n=4", 0.01, g);
w.setWindow(3, 0.0, 0.0, 16, 0.05,
SPACE, 4 * hight, WIDTH - SPACE, 3 * hight + SPACE);
w.axis(3, "", 1, "n=8", 0.01, g);
w.setWindow(4, 0.0, 0.0, 16, 0.05,
SPACE, 5 * hight, WIDTH - SPACE, 4 * hight + SPACE);
w.axis(4, "", 1, "n=16", 0.01, g);
g.setColor(Color.green);
/* メイン */
for (i = 0; i < 5; i++) {
for (j = 1; j <= NUMBER; j++) {
x = central(n);
u = (int) (x * SIZE / n);
f[u] = f[u] + 1;
}
/* ヒストグラムを書く */
for (u = 0; u < SIZE; u++) {
x1 = (double)u / SIZE * n;
y1 = (double)f[u] / NUMBER;
w.line(i, x1, 0, x1, y1, g);
f[u] = 0;
}
n = n * 2;
}
}
public double central(int n) {
int k;
double x = 0.0;
for (k = 0; k < n; k++) {
x = x + Math.random();
}
return (x);
}
}
|
1. プログラムS0330.javaにおいて、指数分布の理論値を用いて、 f[u] / j の項を、 χ2 検定しなさい。
(解答) A0310.java | 実行 |
2. ベルヌーイ試行を連続して行ったとき、 k 回失敗が続いて、 (k+1) 回目にはじめて成功したとします。その時の k の分布 g(k) は p・qk となり、これを幾何分布と呼びます。3.1節と同様に乱数発生により、多数回のベルヌーイ試行の実験を行い、最初に成功する試行回数
k の分布を求め g(k) と比較しなさい。
(解答) A0320.java | 実行 |
|
 |

