 |
|
9. 通信トラヒックのシミュレーション−−待ち合わせシステムと即時系システム−−
|
この章では、前章のシミュレーションプログラムのさまざまな変形により、通信トラヒック問題のシミュレーションを行います。この問題は、オペレションズ
リサーチの分野では、待ち行列の理論として知られているもので、本章は、待ち行列や通信トラヒック問題のシミュレーションを学ぶこととなります。シミュ
レーションの強みは、システムのメカニズムがよく理解できること、理論式では表現できないことも、解答が得られることです。
待ち行列は身近な問題
公衆電話、駅の出札口、食堂のカウンタ、スーパーマーケットのレジ、高速道路の料金所、コンピュータの内部処理、データ通信回線など、待ち行列は身近な
問題で多くの応用があります。8章で作ったプログラムを変形すると、各種のタイプの待ち行列のシミュレーション・プログラムが作れます。
待ち行列を処理する待ち合わせシステムには、非常に数多くの種類があり、次の要素によって分類します。
単位到着の時間的分布
単位とは、公衆電話を使いにくる客、料金所にやってくる車など、サービスを受ける人あるいは物のことです。この単位が到着する時間分布によって待ち行列
の種類を分類します。ランダムに到着するのであれば、ポアソン分布となり、到着間隔は指数分布になることは、すでに3.2節、3.3節で述べました。
サービス時間の分布
到着単位のサービスするに要する時間の長短のことです。ランダムな電話の通話時分のような場合、指数分布となり、工場の生産機械が一定の所要時間で製品を作る場合は、一定のサービス時間となります。
待時と即時
電話は昔は、オペレータに申し込み、回線が空いたら接続すると言う方法でしたが、現在はダイヤルによりすぐ接続できます。前者を待時式、後者を即時式と
言います。待時式の場合、待たされる時間(待ち時間)が問題となりますが、即時式の場合は、途中の回線がふさがっていて話中となる確率(呼損率)が問題と
なります。
また待時系でも、待ち合わせの場所が一杯になったあとに到着した客はたち去らざるを得ないことがあります。待ち合わせ場所が0の場合が即時系に相当します。
到着数の制限(入線数)
到着する単位の数には無制限にいくらでも大きくなり得る場合と、一定の限界がある場合とがあります。切符売場の例は前者であり、機械修理の問題(8章参照)場合は、修理所に到着する機械は、機械の総数より大きくならないので後者の例です。電気通信では入線数と呼びます。
サービス・チャネル数(出線数)
サービス・チャネルは、窓口の数、回線数のことで、機械修理の問題では修理者の組数に相当します.一般に、サービス・チャンネルを増やすには、コストがかかり、お客の満足を損なわずに、この数を最適にすることが問題となります。電気通信では出線数と呼びます。
サービス段数
サービス・システムには、単一段階だけでサービスが終わる場合と、直列的にいくつものサービスを経てサービスが終わる場合があります。
サービス順
待ち行列にならんでいる単位の、サービスの順番の決め方には先着順、ランダム、プライオリティ方式などがあります。
8章で扱った機械修理の問題は、上の分類のよれば、次のとおり待時式入線有限の場合に相当します。
単位到着の時間分布 :機械の故障発生に相当し、指数分布である。
サービス時間の分布 :修理時間に相当し、指数分布である。
待時と即時 :待時である。
到着数の制限 :機械の台数が入線 m に相当する。
サービス・チャネル数 :修理者の組数がサービス・チャネル数に相当する。
サービス段数 :1段
サービス順 :先着順
待時式入線無限大のシステムとは
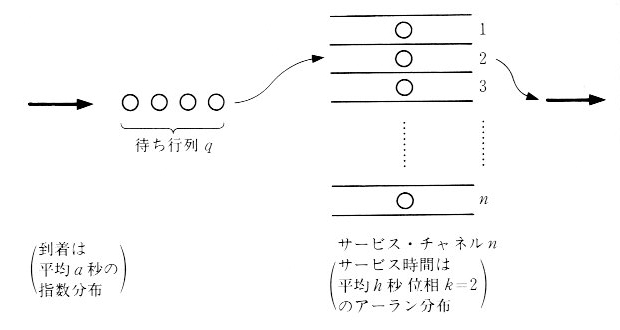
サービス・チャネルが n 回線あるが、到着数の制限はなく、いくらでも大きくなり得る待ち会わせ系を待時式入線無限大のシステムと言います(図9.2.1参照)。これについてシミュレーションをします。前章で作った変化点方式のプログラムs0830.cを母体とします。特に、ポアソン到着、指数保留時間の待時式入線無限大の場合の理論式をErlang C式と呼びます。
| 図9.2.1 待時式入線無限大 |
 |
プログラムのポイント
到着の分布は平均 a 秒(プログラムでは A )ごとの指数分布とし、サービスの分布は平均 h 秒(プログラムでは H )の位相 k=2 アーラン分布にしたがうものとします。プログラムs0920.cが待時式入線無限大の場合のシミュレーションプログラムで、行47から行50までが到着を疑似しています。 tm という次に客が到着するまでの時間が、 0 になった場合、次の tm を指数乱数によりセットし、待ち行列を一つふやします。その時の時刻を tq[q] に書き込んでおきます。
行53から行74がサービスのシミュレーションで、いずれかのサービスチャネルの tn[k] がゼロになるか、サービスチャネルが空き状態の時、待ち行列を見に行き、もし、待ち行列にだれか待っていれば、サービスチャネルをビジー状態にし、
tn[k] にアーラン乱数をセットします。行60により待ち時間 tw を計算し、 tw の和と二乗和を計算します。その後待ち行列が0 でなければ、一つずつ行列を進めます。この部分のアルゴリズムは、前章の機械修理の問題と同様です。行71では、だれも待ち行列になければ、チャンネルを空き状態にします。
時間の進め方も前章で学んだとおりです。
アウトプット
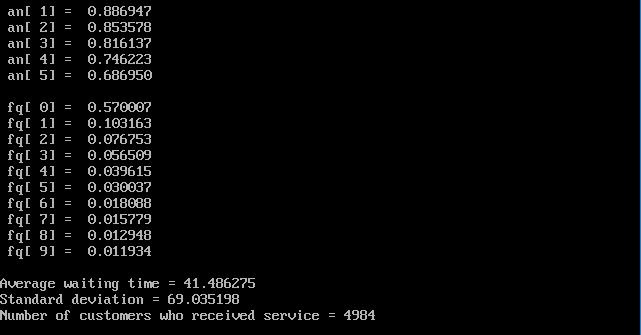
プログラムを実行すると、図9.2.2のように、n=5, a=20, h=80 の場合の、サービス・チャネルの稼働率
an[k] 、待ち行列の長さの分布 fq[q] 、平均待ち時間、待ち時間の標準偏差が得られます。
| 図9.2.2 待時式入線無限大 シミュレーション結果 |
 |
| s0920.c 待時式入線無限大のシステム |
/* s0920.c
* 待時式入線無限大のシステム
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define N 5 /* サービスチャンネル数 */
#define A 20.0 /* 平均到着間隔 */
#define H 80.0 /* 平均サービス時間 */
#define Q_LENGTH 100 /* 待行列の最大の長さ */
#define T_END 100000.0 /* シミュレーションを終る時刻 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i, j, k; /* forのカウンタ */
int sn[N + 1]; /* サービスチャンネルの状態
sn[k]==0:空き,sn[k]==1:ビジー*/
double tn[N + 1]; /* サービスチャンネルが次に変化を起こすまでの時間 */
double an[N + 1] = {0}; /* サービスチャンネルの稼働率 */
double tq[Q_LENGTH] = {0}; /* 待ち行列についた時刻 */
double fq[Q_LENGTH] = {0}; /* 待ち行列が長さqである割合 */
int q = 0; /* 待ち行列の長さ */
int nn = 0; /* サービスを終えた客の数 */
double tm; /* 次に客が到着するまでの時間 */
double tw; /* 待ち時間 */
double x = 0.0; /* twの和 */
double x2 = 0.0; /* twの自乗和 */
double at; /* 時刻増分 */
/* 初期設定 */
srand(21);
tm = - A * log(1.0 - RAND());
for (k = 1; k <= N; k ++) {
sn[k] = 0; tn[k] = INF;
}
/* 開始 */
while (tt <= T_END) {
/* 到着 */
if (fabs(tm) < EPS) {
tm = - A * log(1.0 - RAND());
q = q + 1; tq[q] = tt;
}
/* サービス */
for (k = 1; k <= N; k++) {
if (fabs(tn[k]) < EPS || sn[k] == 0 ) {
/* tn[k]が0あるいはサービスチャンネルが空きのとき*/
if (q > 0) {
sn[k] = 1;
tn[k] = - H / 2.0 * log(RAND() * RAND());
/* 保留時間はアーラン分布 */
tw = tt - tq[1];
x = x + tw;
x2 = x2 + tw * tw;
nn = nn + 1;
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i ++) {
tq[i] = tq[i + 1];
}
}
} else {
sn[k] = 0; tn[k] = INF;
}
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
if (tm < at) at = tm;
for (k = 1; k <= N; k++) {
if (tn[k] < at) at = tn[k];
}
/* 時間を進める */
tm = tm - at;
for (k = 1; k <= N; k++) {
tn[k] = tn[k] - at;
if (sn[k] > 0) { an[k] = an[k] + at;}
}
fq[q] = fq[q] + at;
tt =tt + at;
}
/* 出力 */
printf("\n");
for (k = 1; k <= N; k ++) {
printf(" an[%2d] =%10f \n", k, an[k] / T_END);
}
printf("\n");
for (q = 0; q <= 9; q ++) {
printf(" fq[%2d] =%10f \n", q, fq[q] / T_END);
}
printf("\n");
printf("Average waiting time =%10f\n", x / nn);
printf("Standard deviation =%10f\n", sqrt((x2 - x * x / nn) / nn));
printf("Number of customers who received service = %d\n", nn);
return 0;
}
|
あきらめて立ち去る場合
次の例は,医者の待ち合わせ室や,公衆電話でたくさんの人が待っている時,あきらめて立ち去る場合です。これも,待時式入線無限大のシステムですが,待ち合わせ数が一定値をこえた時に,待ち行列にならばないようなシミュレーション・プログラムを作ります。 これには,プログラムs0920.cに,次の簡単な改造を行います。すなわち待ち合わせ制限数をQ_LENGTHとすれば,Q_LENGTH以上のときは,待ち行列につけないように行51を変更します。
プログラムs0921.cがこの場合のプログラムです。
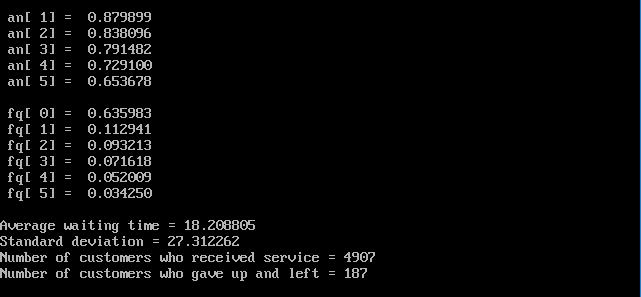
実行すると、図9.2.3のように、あきらめて立ち去った客の数が得られ、平均待ち時間は短くなります。
図9.2.3 あきらめて立ち去る場合
シミュレーション結果 |
 |
| s0921.c 待時式待ち合わせ制限ありのシステム |
/* s0921.c
* 待時式入線無限大のシステム
* (待ち合わせ制限あり)
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define N 5 /* サービスチャンネル数 */
#define A 20.0 /* 平均到着間隔 */
#define H 80.0 /* 平均サービス時間 */
#define Q_LENGTH 5 /* 待行列の最大の長さ */
#define T_END 100000.0 /* シミュレーションを終る時刻 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i, j, k; /* forのカウンタ */
int sn[N + 1]; /* サービスチャンネルの状態
sn[k]==0:空き,sn[k]==1:ビジー*/
double tn[N + 1]; /* サービスチャンネルが次に変化を起こすまでの時間 */
double an[N + 1] = {0}; /* サービスチャンネルの稼働率 */
double tq[Q_LENGTH + 1] = {0}; /* 待ち行列についた時刻 */
double fq[Q_LENGTH + 1] = {0}; /* 待ち行列が長さqである割合 */
int q = 0; /* 待ち行列の長さ */
int nn = 0; /* サービスを終えた客の数 */
int mm = 0; /* あきらめて立ち去った客の数 */
double tm; /* 次に客が到着するまでの時間 */
double tw; /* 待ち時間 */
double x = 0.0; /* twの和 */
double x2 = 0.0; /* twの自乗和 */
double at; /* 時刻増分 */
/* 初期設定 */
srand(21);
tm = - A * log(1.0 - RAND());
for (k = 1;k <= N; k ++) {
sn[k] = 0; tn[k] = INF;
}
/* 開始 */
while (tt <= T_END) {
/* 到着 */
if (fabs(tm) < EPS) {
tm = - A * log(1.0 - RAND());
if (q < Q_LENGTH) {
q = q + 1; tq[q] = tt;
} else { /* 待行列の長さがQ_LENGTH以上の時 */
mm = mm + 1;
}
}
/* サービス */
for (k = 1; k <= N; k++) {
if (fabs(tn[k]) < EPS || sn[k] == 0 ) {
/* tn[k]が0あるいはサービスチャンネルが空きのとき */
if (q > 0) {
sn[k] = 1;
tn[k] = - H / 2.0 * log(RAND() * RAND());/* 保留時間はアーラン分布 */
tw = tt - tq[1];
x = x + tw;
x2 = x2 + tw * tw;
nn = nn + 1;
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i++) {
tq[i] = tq[i + 1];
}
}
} else {
sn[k] = 0; tn[k] = INF;
}
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
if (tm < at) at = tm;
for (k = 1; k <= N; k ++) {
if (tn[k] < at) at = tn[k];
}
/* 時間を進める */
tm = tm - at;
for (k = 1; k <= N; k ++) {
tn[k] = tn[k] - at;
if (sn[k] > 0) { an[k] = an[k] + at;}
}
fq[q] = fq[q] + at;
tt =tt+ at;
}
/* 出力 */
printf("\n");
for (k = 1; k <= N; k ++) {
printf(" an[%2d] =%10f \n", k, an[k] / T_END);
}
printf("\n");
for (q = 0; q <= Q_LENGTH; q ++) {
printf(" fq[%2d] =%10f \n", q, fq[q] / T_END);
}
printf("\n");
printf("Average waiting time =%10f\n", x / nn);
printf("Standard deviation =%10f\n", sqrt((x2 - x * x / nn) / nn));
printf("Number of customers who received service = %d\n", nn);
printf("Number of customers who gave up and left = %d\n", mm);
return 0;
}
|
即時系システムでは損失が問題
今の電話システムは、ダイヤルで直接つながるようになっています。このシステムは即時系システムと呼ばれ、途中の回線が全部ふさがって、話中になる確率
を、十分低くするように設計されています。即時系システムのシミュレーションを実施してみましょう。これは、前節の「あきらめて立ち去る場合」の系で、待
ち行列をゼロとしたものと等価です。
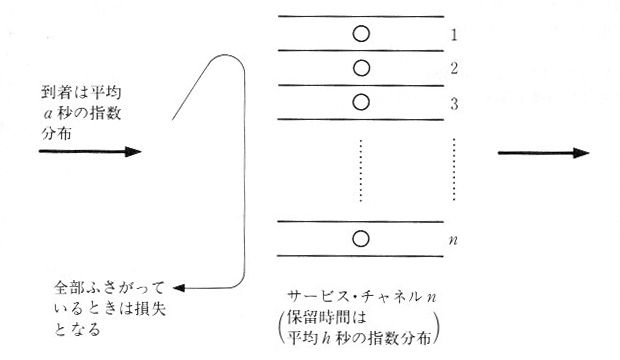
即時系システムの場合、サービス・チャネルが空いている時はサービスをただちに受けられますが、もし全部ふさがっている時は、あきらめることになりま
す。これを損失と言い、電気通信では、特にこれを呼損と言います。(図9.3.1参照)また、電気通信では、サービス時間を保留時間といいます。
| 図9.3.1 即時系システム |
 |
プログラムのポイント
プログラムs0930.cは即時系システムのシミュレーション・プログラムです。行41からが呼びが生起したときの処理で、 tm がゼロになった場合、チャネルをスキャンし、空き回線をさがします。空いていれば、その回線を保留します。全チャネルがビジーのときは、呼損となり、その数
bb をかぞえます。
行59からは、回線が空いたときの処理です。 tn[k] がゼロになった場合、 sn[k] をゼロにします。
出力としては、図9.3.2のように、n=4, a=10, h=10 の場合の、各サービス・チャネルの使用率
an[k] と、呼損率call loss probabilityが得られます。
| 図9.3.2 即時式入線無限大 シミュレーション結果 |
 |
| s0930.c 即時式入線無限大のシステム |
/* s0930.c
* 即時式入線無限大のシステム
* (C) H.Ishikawa 1997 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define N 4 /* サービスチャンネル数 */
#define A 10.0 /* 呼びの発生間隔 */
#define H 10.0 /* 平均保留時間 */
#define T_END 100000.0 /* シミュレーションを終る時刻 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i, j, k; /* forのカウンタ */
int sn[10]; /* サービスチャンネルの状態 */
double tn[10]; /* サービスチャンネルが次に変化を起こすまでの時間 */
double an[10] = {0}; /* サービスチャンネルの稼働率 */
int nn = 0; /* 加わった呼びの数 */
double tm; /* 次に呼びが生起するまでの時間 */
int busy; /* 全チャンネルビジーの時1 */
int bb = 0; /* 損失となった呼びの数 */
double at; /* 時刻増分 */
/* 初期設定 */
srand(2);
tm = - A * log(1.0 - RAND());
for (k = 1;k <= N; k++) {
sn[k] = 0; tn[k] = INF;
}
/* 開始 */
while (tt <= T_END) {
/* 呼びが生起した時の処理 */
if (fabs(tm) < EPS) {
nn = nn + 1;
busy = 1;
for (k = 1; k <= N; k ++) {
if ( sn[k] == 0) { /* 空きチャンネルを探す */
sn[k] = 1;
tn[k] = - H * log(1.0 - RAND());
busy = 0;
break;
}
}
if (busy == 1) {
bb = bb + 1;
}
tm = - A * log(1.0 - RAND());
}
/* チャンネルが空いた時の処理 */
for (k = 1; k <= N; k ++) {
if (fabs(tn[k]) < EPS) {
sn[k] = 0; tn[k] = INF;
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
if (tm < at) at = tm;
for (k = 1; k <= N; k++) {
if (tn[k] < at) at = tn[k];
}
/* 時間を進める */
tm = tm - at;
for (k = 1; k <= N; k++) {
tn[k] = tn[k] - at;
if (sn[k] > 0) { an[k] = an[k] + at;}
}
tt =tt+ at;
}
/* 出力 */
printf("\n");
for (k = 1; k <= N; k ++) {
printf(" an[%2d] =%10f \n", k, an[k] / T_END);
}
printf("\n");
printf("call loss probability =%10f\n", (double)bb / nn);
return 0;
}
|
プライオリティとは
昔の交換手が接続する電話には待時式といって、「至急」と「普通」の種別があり、急いでつないでもらいたい時には、料金は高いが「至急」を申し込みまし
た。これは2つの待ち行列があり、それに優先順位(プライオリティ)をつけておき、優先順位の高い待ち行列を先にサービスし、その待ち行列がなくなったら
低い待ち行列に対しサービスをするというものです。
ここでは、2種類のプライオリティがあり、平均到着率がそれぞれ異なるポアソン分布であり、等しい平均サービス時間をもったアーラン分布サービスの場合
についてシミュレーションをしてみます。(図9.4.1参照)。ただし同じプライオリティの時は先着順にサービスをするものとし、すでにサービス中の客は
たとえあとから優先順位の高い客がきたとしても、継続してサービスを受けるものとします。
| 図9.4.1 プライオリティ待ち合わせシステム |
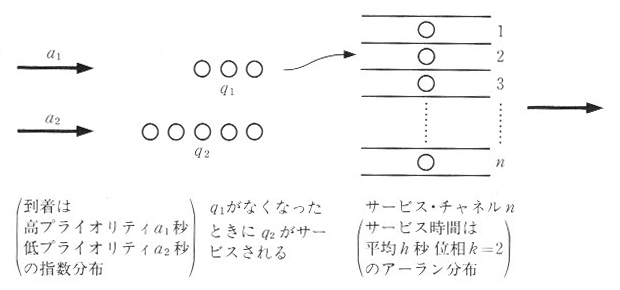 |
プログラムのポイント
図9.4.1のように待ち行列を q1 と q2 の2本用意し、それぞれ平均 a1 , a2 の指数分布到着とします。待時式入線無限大のプログラムs0920.cを改造してプログラムs0940.cを作ります。プログラムs0920.cと異なる点は、行56から行65において,到着の処理が2つの優先度対応となっていること、行67から行101のサービスの処理において待ち行列からとり出す処理が2組あることです。行71で優先度の高い待ち行列
q1 を調べ、もし空であれば行84で低い待ち行列 q2 を見に行きます。
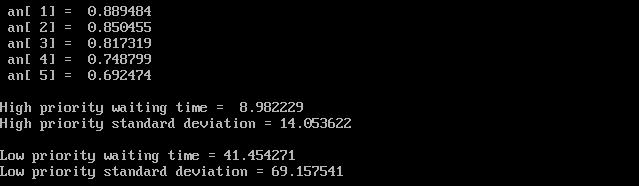
統計出力は、サービス・チャネルごとのの稼働率、優先度ごとの待ち行列の長さの分布、待ち時間の平均、標準偏差を求め、出力します。 図9.4.2のように、n=5. a1=60, a2=30, h=80 の場合についての結果が得られます。
| 図9.4.2 プライオリティ待ち合わせ シミュレーション結果 |
 |
| s0940.c プライオリティ待ち合わシステム |
/* s0940.c
* プライオリティ待ち合わシステム
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define N 5 /* サービスチャンネル数 */
#define A1 60.0 /* 高プライオリティ平均到着間隔 */
#define A2 30.0 /* 低プライオリティ平均到着間隔 */
#define Q_LENGTH 100 /* 待行列の最大の長さ */
#define H 80.0 /* 平均サービス時間 */
#define T_END 100000.0
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i, j, k; /* forのカウンタ */
int sn[N + 1]; /* サービスチャンネルの状態 */
double tn[N + 1]; /* サービスチャンネルが次に変化を起こすまでの時間 */
double an[N + 1] = {0}; /* サービスチャンネルの稼働率 */
double tq1[Q_LENGTH] = {0}; /* 高プライオリティ待ち行列についた時刻 */
double tq2[Q_LENGTH] = {0}; /* 低プライオリティ待ち行列についた時刻 */
double fq1[Q_LENGTH] = {0}; /* 高プライオリティ待ち行列が長さqである割合 */
double fq2[Q_LENGTH] = {0}; /* 低プライオリティ待ち行列が長さqである割合 */
int q1 = 0; /* 高プライオリティ待ち行列の長さ */
int q2 = 0; /* 低プライオリティ待ち行列の長さ */
int nn1 = 0; /* 高プライオリティでサービスを終えた客の数 */
int nn2 = 0; /* 低プライオリティでサービスを終えた客の数 */
double tm1; /* 高プライオリティの次に客が到着するまでの時間 */
double tm2; /* 低プライオリティの次に客が到着するまでの時間 */
double tw1; /* 高プライオリティの待ち時間 */
double tw2; /* 低プライオリティの待ち時間 */
double x1 = 0.0; /* tw1の和 */
double x2 = 0.0; /* tw2の和 */
double x21 = 0.0; /* tw1の自乗和 */
double x22 = 0.0; /* tw2の自乗和 */
double at; /* 時刻増分 */
/* 初期設定 */
srand(2);
tm1 = - A1 * log(1.0 - RAND());
tm2 = - A2 * log(1.0 - RAND());
for (k = 1; k <= N; k++) {
sn[k] = 0; tn[k] = INF;
}
/* 開始 */
while (tt <= T_END) {
/* 高プライオリティ到着 */
if (fabs(tm1) < EPS) {
tm1 = - A1 * log(1.0 - RAND());
q1 = q1 + 1; tq1[q1] = tt;
}
/* 低プライオリティ到着 */
if (fabs(tm2) < EPS) {
tm2 = - A2 * log(1.0 - RAND());
q2 = q2 + 1; tq2[q2] = tt;
}
/* サービス */
for (k = 1; k <= N; k ++) {
if (fabs(tn[k]) < EPS || sn[k] == 0 ) {
/* tn[k]が0あるいはサービスチャンネルが空きのとき */
if (q1 > 0) { /* 高プライオリティの待行列 */
sn[k] = 1;
tn[k] = - H / 2.0 * log(RAND() * RAND());
tw1 = tt - tq1[1];
x1 = x1 + tw1;
x21 = x21 + tw1 * tw1;
nn1 = nn1 + 1;
q1 = q1 - 1;
if (q1 > 0) {
for (i = 1; i <= q1; i++) {
tq1[i] = tq1[i + 1];
}
}
} else if (q2 > 0) { /* 低プライオリティの待行列 */
sn[k] = 1;
tn[k] = - H / 2.0 * log(RAND() * RAND());
tw2 = tt - tq2[1];
x2 = x2 + tw2;
x22 = x22 + tw2 * tw2;
nn2 = nn2 + 1;
q2 = q2 - 1;
if (q2 > 0) {
for (i = 1; i <= q2; i ++) {
tq2[i] = tq2[i + 1];
}
}
} else { /* だれも待っていない */
sn[k] = 0; tn[k] = INF;
}
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
if (tm1 < at) at = tm1;
if (tm2 < at) at = tm2;
for (k = 1; k <= N; k ++) {
if (tn[k] < at) at = tn[k];
}
/* 時間を進める */
tm1 = tm1 - at;
tm2 = tm2 - at;
for (k = 1; k <= N; k ++) {
tn[k] = tn[k] - at;
if (sn[k] > 0) { an[k] = an[k] + at;}
}
fq1[q1] = fq1[q1] + at;
fq2[q2] = fq2[q2] + at;
tt =tt + at;
}
/* 出力 */
printf("\n");
for (k = 1; k <= N; k ++) {
printf(" an[%2d] =%10f \n", k, an[k] / T_END);
}
printf("\n");
for (q1 = 0; q1 <= 9; q1 ++) {
printf(" fq1[%2d] =%10f \n", q1, fq1[q1] / T_END);
}
printf("\n");
for (q2 = 0; q2 <= 9; q2 ++) {
printf(" fq2[%2d] =%10f \n", q2, fq2[q2] / T_END);
}
printf("\n");
printf("High priority waiting time =%10f\n", x1 / nn1);
printf("High priority standard deviation =%10f\n",
sqrt((x21 - x1 * x1 / nn1) / nn1));
printf("\n");
printf("Low priority waiting time =%10f\n", x2 / nn2);
printf("Low priority standard deviation =%10f\n",
sqrt((x22 - x2 * x2 / nn2) / nn2));
return 0;
}
|
定期健康診断の例
サービス設備によっては、複数個のサービス設備が直列にならんでいて、サービスを受ける単位(客)は、順次これらを経由し、全段階のサービスを終えると
いう場合があります。例えば、定期健康診断を受ける場合、受付、体重測定、レントゲン、血圧、問診・・・というようにいくつかの検査を受けますが、1つ1
つの検査の時間(サービス時間)が異なり、また検査員の人数(サービス・チャネル)も異なり、各検査ごとに待ち行列ができます。このような場合の、全体の
サービスが完了するまでの時間を求めるプログラムを作ってみましょう。
プログラムのポイント
9.2節で作った待時系システムが、直列にならんでいるように構成します(図9.5.1参照)。この場合、一人の客に注目し、その客が次々とサービスを受けることを追跡できるようにします。このため、到着する客に1、2、3、・・・と番号をふり最大
MOD となったら、1に戻るようにします。客の番号を mm とし、その値を行列や、サービス・チャネルに、セットするようにします。
| 図9.5.1 サービス段が複数の場合 |
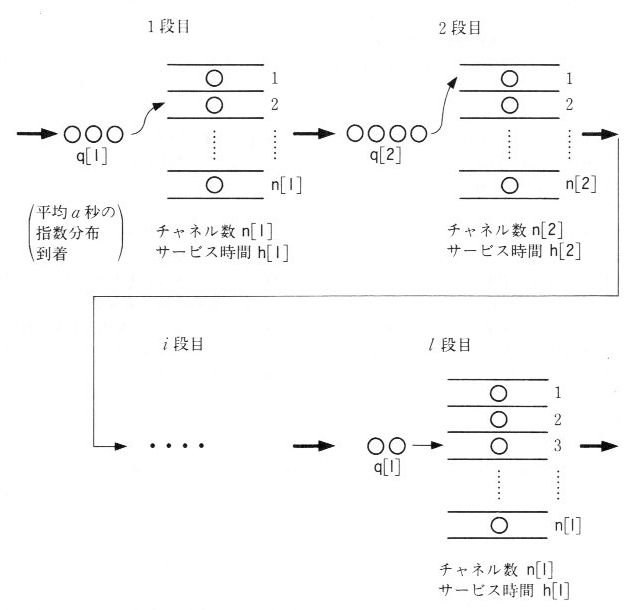 |
プログラムs0950.cはサービス段数が L 段のときのプログラムで、行52からがメインプログラムです。行56から行61でポアソン到着を疑似しており、到着する客に mm=1 から MOD の番号をふり、1段目の待ち行列の q[1] 番目にならばせます。その時の時刻を ta[mm] として記録しておきます。
行64から行93まで、各サービス段 i ごとに、前の段でサービスが終了した客を次の段にならばせます。各段の待ち行列は、行81でとり出し、平均 h[i] の指数分布サービスを受けさせます。行103から行110で、 at ごとの時刻を進行させます。
行71で、最後の段のサービスを終えた客の番号が、 sn[i][k] として入っていますから、 ta[sn[i][k]] がその客の系への到着時間です。現在時刻からそれを引くことによって、その客の全段トータルのサービス時間が計算できます。
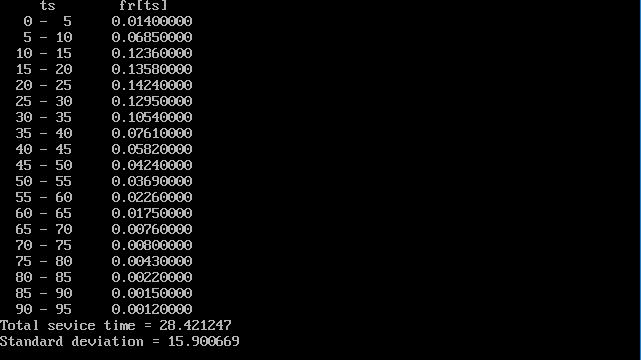
結果の出力図9.5.2のように、全体のサービスを終了する時間Total sevice timeの分布、その平均、標準偏差Standard deviationを出力します。
| 図9.5.2 多段待時式のシステム シミュレーション結果 |
 |
| s0950.c 多段待時式のシステム |
/* s0950.c
* 多段待時式のシステム
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define L 3 /* サービスの段数 */
#define A 5.0 /* 平均到着間隔 */
#define SIZE 5 /* ヒストグラムの大きさ */
#define MOD 128 /* 客の番号の最大値 */
#define NN_END 10000 /* シミュレーションを終る客の数 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i; /* サービス段に対するforのカウンタ */
int k; /* チャンネルに対するforのカウウタ */
int u; /* ヒストグラムに対するforのカウンタ */
int ii; /* 待行列の順番に対するforのカウウタ */
int n[] = {0, 4, 4, 3}; /* 各段ごとのチャンネル数 */
double h[] = {0.0, 10.0, 8.0, 8.0}; /* 各段ごとの平均サービス時間 */
int sn[L + 1][10]; /* サービスチャンネルの状態
* sn[i][k]==0:i段目のkチャンネルは空き
* sn[i][k]==mm: 客mmをサービス中 */
double tn[L + 1][10]; /* サービスチャンネルが次に変化を起こすまでの時間 */
double ta[MOD + 1]; /* 客ごとの到着時刻 */
int q[L + 1] = {0}; /* 各段ごとの待ち行列の長さ */
int sq[L + 1][20]; /* 各段ごとの待ち行列のii番目にならんでいる客の番号 */
int mm = 0; /* 客の番号 1からMODまで */
int nn = 0; /* サービスを終えた客の数 */
double tm; /* 次に客が到着するまでの時間 */
double ts; /* 全サービスを受けたトータルの時間 */
double fr[100] = {0}; /* tsの分布 */
double x = 0.0; /* tsの和 */
double x2 = 0.0; /* tsの自乗和 */
double at; /* 次に状態の変化が起るまでの時間 */
/* 初期設定 */
srand(21);
tm = - A * log(1.0 - RAND());
for (i = 1; i <= L; i ++) {
for (k = 1; k <= n[i]; k ++) {
sn[i][k] = 0; tn[i][k] = INF;
}
}
/* 開始 */
while (nn <= NN_END) {
/* 到着 */
if (fabs(tm) < EPS) {
if (mm < MOD) { mm = mm + 1; } else { mm = 1; }
tm = - A * log(1.0 - RAND());
q[1] = q[1] + 1; sq[1][q[1]] = mm; /* 1段目の待行列にならぶ */
ta[mm] = tt;
}
/* サービス */
for (i = 1; i <= L; i ++) { /* すべての段に対し */
for (k = 1; k <= n[i]; k ++) { /* すべてのチャンネルをスキャン */
if (fabs(tn[i][k]) < EPS) { /* チャンネルが空いた時 */
if (i < L) {
q[i + 1] = q[i + 1] + 1; /* 次の段にならぶ */
sq[i + 1][q[i + 1]] = sn[i][k];
} else { /* 最後の段の場合統計をとる */
ts = tt - ta[sn[i][k]];
x = x + ts;
x2 = x2 + ts * ts;
fr[(int)(ts / SIZE)] = fr[(int)(ts / SIZE)] + 1;/* ヒストグラム */
nn = nn + 1;
}
} else if (sn[i][k] != 0) { /* そのチャンネルがビジーの時は */
continue; /* つぎのkを見に行く */
}
if (q[i] > 0) { /* 待行列から取り出す処理 */
sn[i][k] = sq[i][1];
tn[i][k] = - h[i] * log(1.0 - RAND());
q[i] = q[i] - 1;
if (q[i] > 0) {
for (ii = 1; ii <= q[i]; ii++) {
sq[i][ii] = sq[i][ii + 1];
}
}
} else { /* 待行列に誰もいない */
sn[i][k] = 0; tn[i][k] = INF;
}
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
if (tm < at) at = tm;
for (i = 1; i <= L; i ++) {
for (k = 1; k <= n[i]; k++) {
if (tn[i][k] < at) at = tn[i][k];
}
}
/* 時間を進める */
tm = tm - at;
for (i = 1; i <= L; i ++) {
for (k = 1; k <= n[i]; k ++) {
tn[i][k] = tn[i][k] - at;
}
}
/* 表示
この行123までのコメントをいかせば、変化のあるごとに,何番目の客が何段目
のどのチャンネルでサービスを受けているか表示する
printf("%6.2f ",tt);
for (i = 1; i <= L; i ++) {
for (k = 1; k <= n[i]; k ++) printf(" %3d",sn[i][k]);
printf("%3d",q[i]);
}
printf(" ");
printf(" %10f",ts);
printf("\n");
*/
tt =tt + at;
}
/* ヒストグラムの出力 */
printf(" ts fr[ts]\n");
for (u = 0; u < 19 ; u++) {
printf(" %2d - %2d %1.8f\n",
u*SIZE,(u+1)*SIZE, (double)(fr[u])/NN_END);
}
printf("Total sevice time =%10f\n", x / NN_END);
printf("Standard deviation =%10f\n", sqrt((x2 - x * x / NN_END) / NN_END));
return 0;
}
|
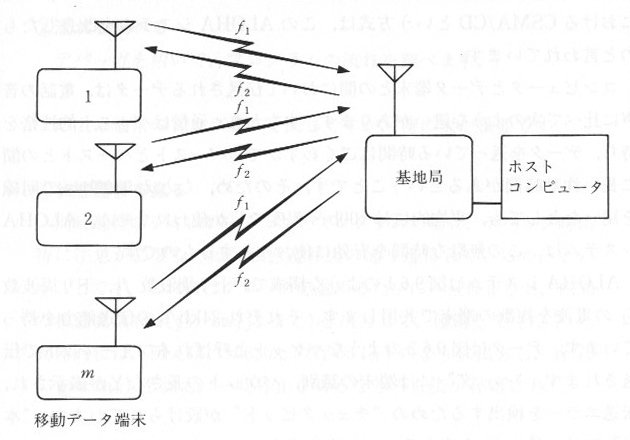
ALOHAシステムとは
ALOHAシステム(文献(14))
は、無線を用いたデータ伝送システムで、技術史に残る歴史的な方式です。ランダムアクセスという方式により複数の端末が、1つの電波を共用しているのが特
徴で、ハワイ大学で1968年からUHF無線による実験がおこなわれました。最近、私たちがよく用いる、ローカルエリアネットワーク(LAN)における
CSMA/CDという方式は、このALOHAシステムを改良したものと言われています。
コンピュータとデータ端末との間において伝送されるデータは、次のように電話の音声とは違いがあります。すなわち、通信がバースト的性格を待ち、データ
を送っている時間はごくわずかで、バーストとバーストとの間に長い沈黙時間があるということです。これは、たとえ9600b/sの回線を用いるとしても、
平均的には、100b/s程度でしか使われていません。ALOHAシステムでは、この無駄な時間を有効に使おうとするものです。
ALOHAシステムは、図9.6.1のような構成で、のぼり周波数 f1 、くだり周波数 f2 の電波
を複数の端末で共用します。それぞれ24kb/sの伝送能力を持っています。データは図9.6.2のようなパケットとよばれるフォーマットで伝送されま
す。”ヘッダ”には端末の識別、パケットの長さなどが表示され、伝送エラーを検出するための”チェックビット”が設けられています。”本文”には、最大
80文字のデータが入ります。
コンピュータから下りのパケットを伝送するには、それほどの工夫はいりません。すべての端末は
f2
の周波数を受信し、ヘッダが自分の識別番号の場合だけ、とり込めばよいのです。逆に各端末から、のぼりのパケットを送信する場合は、約束事が必要です。各
端末は他の端末が送信中がどうかにかかわらず、送信します。送信中に他端末が送信を開始しなければ、データ伝送は成功します。しかし送信中に他の端末がパ
ケットを送信すると、データは混信し正しく受信されません。このような、重複がおこったとき、どちらの端末から発信されたパケットも誤りが生じ、チェック
ビットで検出されます。その時はタイミングをおいてから再送します。使用中の端末数が増すにつれ、干渉の数、したがって再送の数が増大し、ついにチャンネ
ルは繰り返し送られてくるパケットで一杯になり、容量限界となります。
このように、ALOHAシステムは、制約はありますが、わずか2種類の周波数だけで、たくさんの端末とデータ伝送するようにした、画期的な方式でした。
| 図9.6.1 ALOHAシステムの構成 |
 |
| 図9.6.2 パケットのフォーマット |
 |
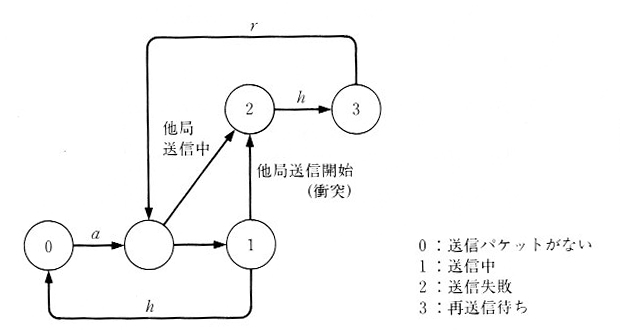
状態図
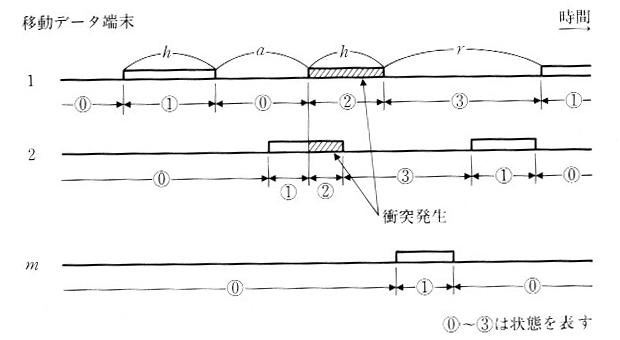
各端末の状態図は図9.6.3のようになります。状態 0 は、送るべきデータがない状態、状態 1 はデータを送信中の状態。状態 2 はデータを送信しているが、他端末も送信中のため不成功に終わるであろう状態。状態
3 は再送信を待っている状態。これらの動作チャートを図9.6.4に表わしています。成功する場合は、状態0→状態1→状態0の繰り返しとなりますが、もし状態1にあるとき、他端末が送信を開始すると状態2に移り、その後、状態3により、再送信待ちとなります。
これらの図で a は、次のデータが発生するまでの時間、 h は平均パケット長、 r は再送信のタイミングで、それぞれ指数分布と仮定します。 r
も指数分布とするのは、一定のタイミングで再送すると、ふたたび他の端末と衝突するからで、端末ごとに再送タイミングを異なった値にするためです。
| 図9.6.3 ALOHAシステムの状態図 |
 |
| 図9.6.4 ALOHAシステムの動作 |
 |
プログラムのポイント
これらの状態を各端末ごとに s[j] という配列で表わし、その状態にとどまっている時間をもう1つの配列 t[j] で表わします。すなわち s[1]=0, t[1]=30 ということは、1番の端末は0 の状態にあり、それが30ミリ秒続くことを示します。
プログラムs0960.cは、ALOHAシステムのシミュレーション・プログラムで、行61からがメインプログラムです。行64で、 j を変えてみて、 t[j]=0 すなわち状態変化の起こる端末を探します。そして、その端末の状態0、1、2、3に従って、図9.6.3に示した状態変化をおこすよう記述します。たとえ
ば、これまで状態0 であった場合、行71のように他の端末すべてが送信中かどうか調べ、もしそのような端末が見つかれば、その端末と自分の端末を送信失敗の状態2にします。
全ての端末が送信中でなければ(プログラムでは、 ss==0 ならば)、状態1に移ります。
このプログラムでは、送信完了したパケットの数が NN_END になるまで、シミュレーションをしますが、そのあと、平均パケット長を変えて、シミュレーションを続けます。
| s0960.c アロハシステム |
/* s0960.c
* アロハシステム
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() */
#include "compati.h"
#include "window.h"
#define M 8 /* 端末の数 */
#define R 10 /* 再送信タイミング */
#define NN_END 5000 /* シミュレーションを終るパケットの数 */
#define H_END 0.8 /* hの最大 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt; /* シミュレーション時刻 */
double a; /* パケットを送り終って次の送るべきパケットが
発生するまでの平均時間 */
double h; /* 平均パケット伝送時間 */
int i; /* forのカウンタ */
int j; /* forのカウンタ */
int s[M + 1]; /* 端末の状態 s[j]=0,1,2,3 */
double t[M + 1]; /* 端末が次に変化を起こすまでの時間 */
double tr[M + 1]; /* 再送パケット伝送時間 */
double t0[M + 1]; /* パケット伝送開始時刻 */
int ss; /* いずれかの端末が送信中の時ss=1
そうでないときss=0 */
int nn; /* 送信完了したパケットの数 */
double tw; /* 待ち時間の合計 */
double ts; /* 送信成功したパケット伝送時間の合計 */
double at; /* 次に状態の変化が起るまでの時間 */
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,H_END,0.2,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "h", 0.2, "through put", 0.05);
SetWindow(1, 0.0,0.0,H_END,100,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "h", 0.2, "waiting time", 20);
MoveTo(0, 0.0, 0.0);
MoveTo(1, 0.0, 0.0);
setlinestyle(0, 0, 2);
a = 10;
h = 0.0;
while (h <= H_END) {
/* 初期設定 */
srand(3);
h = h + 0.05; ss = 0; nn = 0; tt = 0; tw = 0.0; ts = 0.0;
for (j = 1; j <= M; j ++) {
s[j] = 0; t[j] = - a * log(1.0 - RAND());
}
/* 開始 */
while (nn <= NN_END) {
for (j = 1; j <= M; j ++) {
if (fabs(t[j]) < EPS) {
switch(s[j]) {
case 0: /* 送信パケット発生 */
t[j] = - h *log(1 - RAND());
tr[j] = t[j];
t0[j] = tt;
ss = 0;
for (i = 1 ;i <= M; i ++) {
if (s[i] == 1 || s[i] == 2 ) { /* 他局送信中 */
s[i] = 2; /* 他局送信失敗 */
s[j] = 2; /* 自局送信失敗 */
ss = 1;
break;
}
}
if (ss == 0) {
s[j] = 1; /* 送信中 */
}
break;
case 1: /* 送信完了 */
nn = nn + 1; /* 統計をとる */
tw = tw + (tt - t0[j]);
ts = ts + tr[j];
s[j] = 0;
t[j] = - a * log(1 - RAND());
break;
case 2: /* 送信失敗 */
s[j] = 3;
t[j] = - R * log(1 - RAND());
break;
case 3: /* 再送信開始 */
ss = 0;
for (i = 1; i <= M; i ++) {
if ( s[i] == 1 || s[i] == 2) {
s[i] = 2;
s[j] = 2; t[j] = tr[j];
ss = 1;
break;
}
}
if (ss == 0) {
s[j] = 1; t[j]= tr[j];
ss = 1;
}
break;
}
}
}
/* 時間を進める */
at = INF;
for (j = 1; j <= M; j ++) {
if (t[j] < at) at = t[j];
}
for (j = 1; j <= M; j ++) {
t[j] = t[j] - at;
}
/* 表示 */
/* この部分を生かせば、状態変化があるたびに、各端末の状態を表示する
printf("%6.4f ",tt);
for (j = 1; j <= M; j ++) {
printf(" %3d",s[j]);
}
printf("%2d ",ss);
printf("\n");
*/
tt =tt+ at;
}
/* 出力 */
LineTo(0, h, ts / tt);
LineTo(1, h, tw / nn);
}
getch();
closegraph();
return 0;
}
|
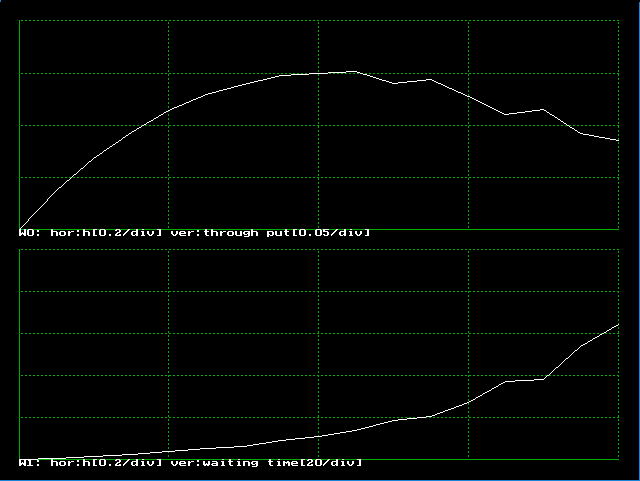
アウトプット
シミュレーションプログラムs0960.cを実行しその結果を見ましょう。ALOHAシステムにおいては、多数のパケットが加わ り、あるいはパケット長が長くなり、電波に対する負荷が大きくなると、パケット同志の衝突がおこり再送によりさらに送信パケット数が増大し、悪循環となりま す。すなわち、負荷が小さい間は、負荷とともに、うまく届いたデータ量(これをスループットと言います)は、増えていきますが、ある限界をこえると、逆に スループットは下がってしまいます。
図9.6.5のウインドウ0は、縦軸にスループット(全体の時間に対するうまく届いたパケット伝送時間の総量)を、パケットの長さをかえて(これが負荷に相当する)表示しています。確かに負性特性を示しているのが解ります。ウインドウ1の縦軸に、再送信のため、待たされた時間を含んだ送信時間を示しています。負荷が大きくなるとこの時間が急速に増大しているのが解ります。
ALOHAシステムは、負荷の小さい状態で使うべきものでが、このような特性からALOHAシステムは、現在、実用的でないとされています。しかしなが
ら、衝突防止のアルゴリズムがさまざま発明されました。特にローカルエルアネットワーク(LAN)でよく使われる、CSMA/CDという方式は、LANの
同軸ケーブルを1つを無線空間と考え、パケットを送信する前に他の端末が、パケットを出していないかどうか検出し、衝突を回避する方式です。ALOHAシ
ステムをベースに開発され、普及したシステムの一例です。
| 図9.6.5 ALOHAシステム シミュレーション結果 |
 |
ポーリング・システムとは
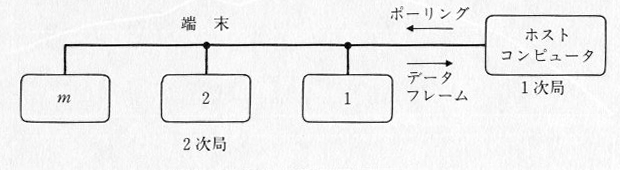
ポーリング・システムは、コンピュータと複数の端末が同一の回線を共用してデータ通信を行う通信システムです。図9.7.1のようにコンピュータと端末
が接続されていて、端末はコンピュータの指示にしたがってデータを送信します(この送る単位をフレームと言います)。指示のし方は、端末1、2、
3、・・・の順にコンピュータが問いかけ、端末はもし送るべきデータがあればデータフレームを、もしなければ“無し”というフレームを送信します。この問
いかけのことをポーリングと言います。また、ホストコンピュータのことを1次局、端末のことを2次局と呼びます。同一の回線を共用しますから、経済的な通
信システムを構成できますが、各端末が送るデータフレームが多くなると、なかなかポーリングがまわってこないので、送信が待たされることになります。
| 図9.7.1 ポーリング・システム |
 |
このようなシステムのシミュレーションを行い、回線の使用能率、単位時間あたりの伝送フレーム数、送信が待たされる平均時間を求めることにしましょう。
状態図
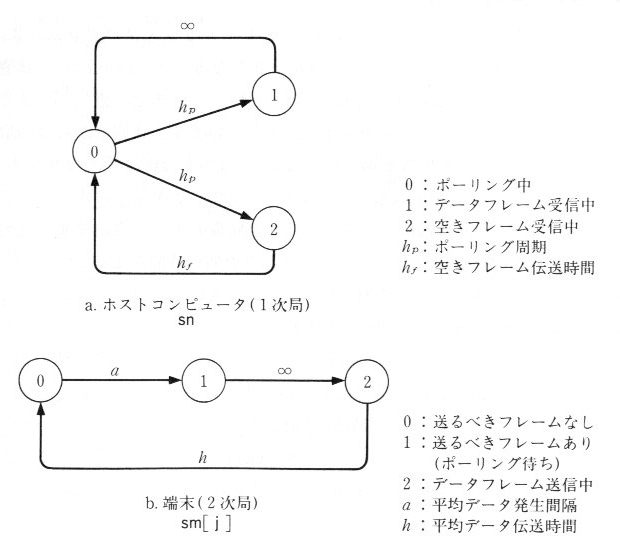
まず端末側、すなわち、2次局側の状態を説明します。図9.7.2bに示すとおり、平均
a ミリ秒指数分布で、データを発生することとします。送るべきフレームのある状態を状態1とし、1次局からのポーリング待ちとなります。1次局からの順番で、ポーリングがまわってくると、状態2のデータフレーム送信中の状態になります。
ホストコンピュータ側すなわち、1次局の状態はやや複雑で、 hp という周期で、 p 番目の端末にポーリングのフレームを送出します。もし、その端末に送信すべきデータがあれば、自分は状態1となり、データを受信します。端末に送るべきデータがなければ、データ無しのフレームを受信する状態2となります。そして、
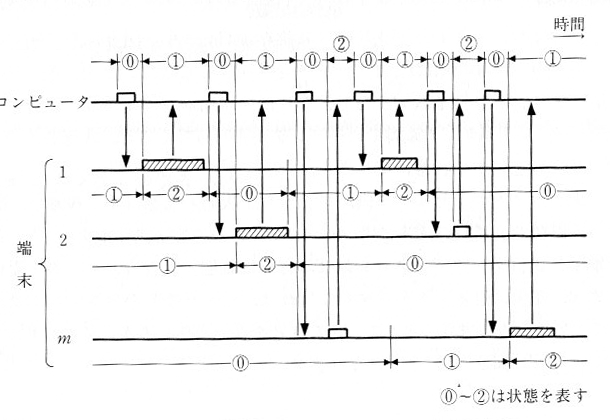
p の番号を1つ増やします。タイムチャートに書けば、図9.7.3のようになります。
| 図9.7.2 ポーリング・システムの状態遷移図 |
 |
| 図9.7.3 ポーリング・システムの動作 |
 |
プログラムのポイント
プログラムs0970.cがポーリング・システムのシミュレーション・プログラムです。行68からが1次局を疑似しており tn が0となるごとに図9.7.2aの状態変化を起こします。 case 0, 1, 2 でそれぞれ、それまで、状態0、1、2であった場合に、 tn が0の時の変化を記述しています。状態0からは、2次局 p におくるべきデータがある場合、行72のように sn は1となります。このとき、 tn=INF と無限大していますが、行98で、2次局 j にポーリングがかかったとき、 tn に送信すべきデータ伝送時間がセットされます。状態1、2からの変化は同一で、行80でポーリング周期の時間を tn にセットし、 sn=0 としています。このとき、行81のように、次にポーリングをかける p の番号を最大 M の範囲で1つ増加させます。
行87からが2次局の各端末を疑似するプログラムで、 sm[j] の値にしたがって case 0, 1, 2 により状態変化を記述します。 case 0 で sm[j] が0から1に変化します。行91で sm[j]=1; tm[j]=INF としていますが、1次局側の行73でポーリングをかけた時、 tm[p]=0 としているところがポイントです。また、2次局が、状態0から1に変化したとき、その時の時刻を行92で t0[j] にセットしておき、あとで case 1 により行103で送信を完了したときの時刻との差を待ち時間として計算します。
アウトプット
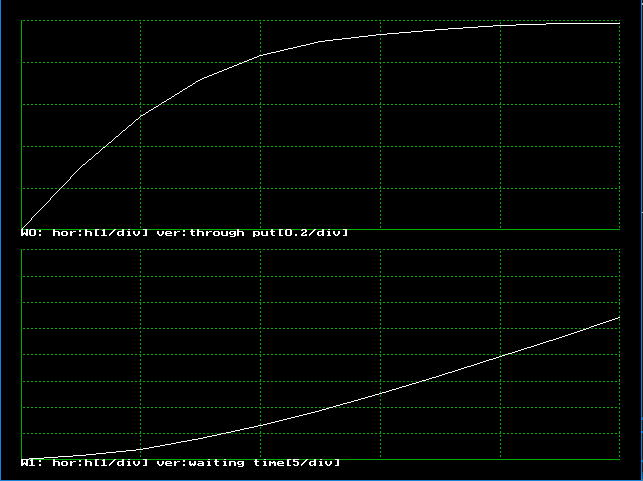
図9.7.4のように、2つのウインドウに、それぞれ、平均フレーム長(負荷に相当)に対するスループットと、同じく負荷に対する待ち時間が表示されています。負荷が重くなると、ほぼ回線は100%近く利用され、ALOHAシステムにくらべ、安定な特性を示しています。
| 図9.7.4 ポーリングシステム シミュレーション結果 |
 |
| s0970.c ポーリングシステム |
/* s0970.c
* ポーリングシステム
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() */
#include "compati.h"
#include "window.h"
#define M 8 /* 2次局の数 */
#define HP 0.001 /* ポーリング周期 */
#define HF 0.001 /* 空きフレーム伝送時間 */
#define NN_END 100 /* シミュレーションをおわるフレームの数 */
#define H_END 5.0 /* hの最大 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
double a; /* フレームを送り終ってから次の
フレームが発生するまでの平均時間 */
double h; /* 平均データ伝送時間 */
int j; /* forのカウンタ */
int sn; /* 1次局の状態 */
double tn; /* 1次局が次に変化を起こすまでの時間 */
int sm[M + 1]; /* 2次局の状態 */
double tm[M + 1]; /* 2次局が次に変化を起こすまでの時間 */
double t0[M + 1]; /* ポーリング待ち状態に入った時刻 */
double tf[M + 1]; /* 送信フレーム時間 */
int p; /* ポーリングをかけている2次局の番号 */
int nn; /* 送信完了したフレームの数 */
double tw; /* 待ち時間の合計 */
double ts; /* 送信したフレーム時間の合計 */
double at; /* 次に状態の変化が起るまでの時間 */
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,H_END,1,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "h", 1.0, "through put", 0.2);
SetWindow(1, 0.0,0.0,H_END,40,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "h", 1.0, "waiting time", 5.0);
MoveTo(0, 0.0, 0.0);
MoveTo(1, 0.0, 0.0);
setlinestyle(0, 0, 2);
a = 10;
h = 0.0;
while (h < H_END) {
/* 初期設定 */
srand(21);
h = h + 0.5; nn = 0; tt = 0; tw = 0.0; ts = 0.0;
sn = 0; tn = HP;
for (j = 1; j <= M; j ++) {
sm[j] = 0; tm[j] = - a * log(1.0 - RAND());
}
p = 1;
/* 開始 */
while (nn < NN_END) {
/* 1次局のシミュレーション */
if (fabs(tn) < EPS) {
switch(sn) {
case 0: /* ポーリング完了 */
if (sm[p] == 1) { /* 2次局pに送るべきデータがある場合 */
sn = 1; tn = INF; /* 1次局は状態1へ */
tm[p] = 0.0; /* 2次局pのtm[p]を0とする */
} else {
sn = 2; tn = HF; /* 1次局は状態2へ */
}
break;
case 1: /* データフレーム受信完了 */
case 2: /* 空フレーム受信完了 */
sn = 0; tn = HP; /* 1次局は状態0へ */
if (p < M) { p = p + 1;} else {p = 1;} /* ポーリング番号を1増加 */
break;
}
}
/* 2次局のシミュレーション */
for (j = 1; j <= M; j ++) {
if (fabs(tm[j]) < EPS) {
switch(sm[j]) {
case 0: /* 送るべきフレーム発生 */
sm[j] = 1; tm[j] = INF; /* 状態1へ */
t0[j] = tt;
break;
case 1: /* ポーリング待へ */
/* 次の送信フレーム */
sm[j] = 2; tm[j] = - h * log(1.0 - RAND());
tf[j] = tm[j];
tn = tm[j]; /* 1次局のtnをtm[j]と同じ値とする */
break;
case 2: /* フレーム送信完了 */
/* 統計をとる */
nn = nn + 1;
tw = tw + (tt - t0[j]);
ts = ts + tf[j];
sm[j] = 0; /* 状態0へ */
tm[j] = - a * log(1.0 - RAND());
break;
}
}
}
/* 時間を進める */
at = INF;
if (tn < at) at = tn;
for (j = 1; j <= M; j ++) {
if (tm[j] < at) at = tm[j];
}
tn = tn - at;
for (j = 1; j <= M; j ++) {
tm[j] = tm[j] - at;
}
tt =tt + at;
}
/* 出力 */
LineTo(0, h, ts / tt);
LineTo(1, h, tw / nn);
} /* 次のhへ */
getch();
closegraph();
return 0;
}
|
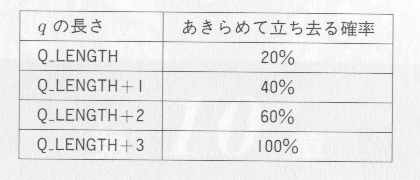
1. プログラムs0921.cで、待ち行列の長さ q が q1 をこえた時、次の確率で待ち合わせをあきらめる場合についてシミュレートしなさい。
| 表e.9.1 |
 |
(解答)
| a0910.c 9章1.解答 待時式入線無限大のシステム |
/* a0910.c 9章1.解答
* 待時式入線無限大のシステム
* (待ち合わせ制限あり)
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define N 5 /* サービスチャンネル数 */
#define A 20.0 /* 平均到着間隔 */
#define H 80.0 /* 平均サービス時間 */
#define Q_LENGTH 5 /* 待行列の最大の長さ */
#define T_END 100000.0 /* シミュレーションを終る時刻 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
#define P0 0.2 /* あきらめて立ち去る確率 */
#define P1 0.4 /* あきらめて立ち去る確率 */
#define P2 0.8 /* あきらめて立ち去る確率 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i, j, k; /* forのカウンタ */
int sn[N + 1]; /* サービスチャンネルの状態
sn[k]==0:空き,sn[k]==1:ビジー*/
double tn[N + 1]; /* サービスチャンネルが次に変化を起こすまでの時間 */
double an[N + 1] = {0}; /* サービスチャンネルの稼働率 */
double tq[Q_LENGTH + 5] = {0}; /* 待ち行列についた時刻 */
double fq[Q_LENGTH + 5] = {0}; /* 待ち行列が長さqである割合 */
int q = 0; /* 待ち行列の長さ */
int nn = 0; /* サービスを終えた客の数 */
int mm = 0; /* あきらめて立ち去った客の数 */
double tm; /* 次に客が到着するまでの時間 */
double tw; /* 待ち時間 */
double x = 0.0; /* twの和 */
double x2 = 0.0; /* twの自乗和 */
double at; /* 時刻増分 */
/* 初期設定 */
srand(21);
tm = - A * log(1.0 - RAND());
for (k = 1;k <= N; k ++) {
sn[k] = 0; tn[k] = INF;
}
/* 開始 */
while (tt <= T_END) {
/* 到着 */
if (fabs(tm) < EPS) {
tm = - A * log(1.0 - RAND());
if (q < Q_LENGTH) {
q = q + 1; tq[q] = tt;
} else if ((q == Q_LENGTH) && (P0 < RAND())) {/* 以下をs0921.cから修正 */
q = q + 1; tq[q] = tt;
} else if ((q == Q_LENGTH + 1) && (P1 < RAND())) {
q = q + 1; tq[q] = tt;
} else if ((q == Q_LENGTH + 2) && (P2 < RAND())) {
q = q + 1; tq[q] = tt;
} else {
mm = mm + 1;
}
}
/* サービス */
for (k = 1; k <= N; k++) {
if (fabs(tn[k]) < EPS || sn[k] == 0 ) {
/* tn[k]が0あるいはサービスチャンネルが空きのとき */
if (q > 0) {
sn[k] = 1;
tn[k] = - H / 2.0 * log(RAND() * RAND());/* 保留時間はアーラン分布 */
tw = tt - tq[1];
x = x + tw;
x2 = x2 + tw * tw;
nn = nn + 1;
q = q - 1;
if (q > 0) {
for (i = 1; i <= q; i++) {
tq[i] = tq[i + 1];
}
}
} else {
sn[k] = 0; tn[k] = INF;
}
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
if (tm < at) at = tm;
for (k = 1; k <= N; k ++) {
if (tn[k] < at) at = tn[k];
}
/* 時間を進める */
tm = tm - at;
for (k = 1; k <= N; k ++) {
tn[k] = tn[k] - at;
if (sn[k] > 0) { an[k] = an[k] + at;}
}
fq[q] = fq[q] + at;
tt =tt+ at;
}
/* 出力 */
printf("\n");
for (k = 1; k <= N; k ++) {
printf(" an[%2d] =%10f \n", k, an[k] / T_END);
}
printf("\n");
for (q = 0; q <= Q_LENGTH + 4; q ++) {
printf(" fq[%2d] =%10f \n", q, fq[q] / T_END);
}
printf("\n");
printf("平均待ち時間 =%10f\n", x / nn);
printf("待ち時間の標準偏差 =%10f\n", sqrt((x2 - x * x / nn) / nn));
printf("サービスを受けた客の数 = %d\n", nn);
printf("あきらめて立ち去った客の数 = %d\n", mm);
return 0;
}
|
2. 入線が有限 m 、出線 n の 場合の即時系システムのシミュレーション・プログラムを作りなさい。
(解答)
| a0920.c 9章2.解答 即時式入線有限のシステム |
/* a0920.c 9章2.解答
* 即時式入線有限のシステム
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() sqrt()*/
#include "compati.h"
#define M 10 /* 入回線数 */
#define N 4 /* 出回線数 */
#define A 100.0 /* 呼びの発生間隔 */
#define H 10.0 /* 平均保留時間 */
#define T_END 100000.0 /* シミュレーションを終る時刻 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt = 0.0; /* シミュレーション時刻 */
int i, j, k; /* forのカウンタ */
int sn[10]; /* 出回線の状態 */
double tn[10]; /* 出回線が次に変化を起こすまでの時間 */
double an[10] = {0}; /* 出回線の稼働率 */
int nn = 0; /* 加わった呼びの数 */
double tm[10]; /* 次に呼びが生起するまでの時間 */
int busy; /* 全チャンネルビジーの時1 */
int bb = 0; /* 損失となった呼びの数 */
double at; /* 時刻増分 */
/* 初期設定 */
srand(2);
for (j = 1; j <= M; j ++) {
tm[j] = - A * log(1.0 - RAND());
}
for (k = 1;k <= N; k ++) {
sn[k] = 0; tn[k] = INF;
}
/* 開始 */
while (tt <= T_END) {
/* 呼びが生起した時の処理 */
for (j = 1; j <= M; j ++) {
if (fabs(tm[j]) < EPS) {
nn = nn + 1;
busy = 1;
for (k = 1; k <= N; k ++) {
if ( sn[k] == 0) { /* 空き出回線を探す */
sn[k] = 1;
tn[k] = - H * log(1.0 - RAND());
busy = 0;
break;
}
}
if (busy == 1) {
bb = bb + 1;
}
tm[j] = - A * log(1.0 - RAND());
}
}
/* 出回線が空いた時の処理 */
for (k = 1; k <= N; k ++) {
if (fabs(tn[k]) < EPS) {
sn[k] = 0; tn[k] = INF;
}
}
/* 次に状態変化の起る時刻を求める */
at = INF;
for (j = 1; j <= M; j ++) {
if (tm[j] < at) at = tm[j];
}
for (k = 1; k <= N; k++) {
if (tn[k] < at) at = tn[k];
}
/* 時間を進める */
for (j = 1; j <= M; j ++) {
tm[j] = tm[j] - at;
}
for (k = 1; k <= N; k++) {
tn[k] = tn[k] - at;
if (sn[k] > 0) { an[k] = an[k] + at;}
}
tt =tt+ at;
}
/* 出力 */
printf("\n");
for (k = 1; k <= N; k ++) {
printf(" an[%2d] =%10f \n", k, an[k] / T_END);
}
printf("\n");
printf("呼損率 =%10f\n", (double)bb / nn);
return 0;
}
|
3. ALOHAシステムは、移動データ端末は他の端末の状態におかまいなく、パケットを送信しますが、他の端末がパケットを送信していないことを確認したときだけ、パケットを送信する方式について、シミュレーションしなさい。
(解答)
| a0930.c 9章3.解答 キャリア・センス形アロハシステム |
/* a0930.c 9章3.解答
* キャリア・センス形アロハシステム
* (C) H.Ishikawa 1994 2018
* 完全にキャリア(他局の電波)を、センスできる場合のシミュレーション。
* 実際には、同時に送信開始してしまうことがおこり、送信失敗がありうる。
*/
#include <stdio.h> /* printf() */
#include <math.h> /* log() fabs() */
#include "compati.h"
#include "window.h"
#define M 8 /* 端末の数 */
#define R 10 /* 再送信タイミング */
#define NN_END 5000 /* シミュレーションを終るパケットの数 */
#define H_END 0.8 /* hの最大 */
#define INF 1.0e100 /* 十分大きい値 */
#define EPS 1.0e-100 /* 十分小さい値 */
int main(void)
{
double tt; /* シミュレーション時刻 */
double a; /* パケットを送り終って次の送るべきパケットが
発生するまでの平均時間 */
double h; /* 平均パケット伝送時間 */
int i; /* forのカウンタ */
int j; /* forのカウンタ */
int s[M + 1]; /* 端末の状態 s[j]=0,1,3
* 0:送信パケット無し
* 1:送信中
* 3:再送信待ち (2:欠番)*/
double t[M + 1]; /* 端末が次に変化を起こすまでの時間 */
double tr[M + 1]; /* 再送パケット伝送時間 */
double t0[M + 1]; /* パケット伝送開始時刻 */
int ss; /* いずれかの端末が送信中の時ss=1
そうでないときss=0 */
int nn; /* 送信完了したパケットの数 */
double tw; /* 待ち時間の合計 */
double ts; /* 送信成功したパケット伝送時間の合計 */
double at; /* 次に状態の変化が起るまでの時間 */
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,H_END,0.5,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "h", 0.2, "through put", 0.05);
SetWindow(1, 0.0,0.0,H_END,20,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "h", 0.2, "waiting time", 5);
MoveTo(0, 0.0, 0.0);
MoveTo(1, 0.0, 0.0);
setlinestyle(0, 0, 2);
a = 10;
h = 0.0;
while (h <= H_END) {
/* 初期設定 */
srand(3);
h = h + 0.05; ss = 0; nn = 0; tt = 0; tw = 0.0; ts = 0.0;
for (j = 1; j <= M; j ++) {
s[j] = 0; t[j] = - a * log(1.0 - RAND());
}
/* 開始 */
while (nn <= NN_END) {
for (j = 1; j <= M; j ++) {
if (fabs(t[j]) < EPS) {
switch(s[j]) {
case 0: /* 送信パケット発生 */
t[j] = - h *log(1 - RAND());
tr[j] = t[j];
t0[j] = tt;
if (ss == 1) { /* キャリアをセンス */
s[j] = 3; /* 再送信待ちへ */
t[j] = - R * log(1-RAND());
} else {
s[j] = 1; /* 送信中へ */
ss = 1;
}
break;
case 1: /* 送信完了 */
nn = nn + 1; /* 統計をとる */
tw = tw + (tt - t0[j]);
ts = ts + tr[j];
s[j] = 0;
ss = 0; /* 電波空いた */
t[j] = - a * log(1 - RAND());
break;
case 3: /* 再送信開始 */
if (ss == 1) { /* キャリアをセンス */
s[j] = 3; /* 再送信待ちへ */
t[j] = - R * log(1-RAND());
} else {
s[j] = 1; /* 送信中へ */
ss = 1;
}
break;
}
}
}
/* 時間を進める */
at = INF;
for (j = 1; j <= M; j ++) {
if (t[j] < at) at = t[j];
}
for (j = 1; j <= M; j ++) {
t[j] = t[j] - at;
}
/* 表示 */
/* この部分を生かせば、状態変化があるたびに、各端末の状態を表示する
printf("%6.4f ",tt);
for (j = 1; j <= M; j ++) {
printf(" %3d",s[j]);
}
printf("%2d ",ss);
printf("\n");
*/
tt =tt + at;
}
/* 出力 */
LineTo(0, h, ts / tt);
LineTo(1, h, tw / nn);
}
getch();
closegraph();
return 0;
}
|
|
 |
