 |
通信の分野では、伝送路や電子管などから発生するランダムな雑音により、妨害をうけて、正確に信号が受信されなくなることがあります。この章では、雑音
をコンピュータで作りだし、雑音の中から信号を分離する実験をやってみましょう。これは、最近ディジタル信号処理といって、発展の著しい分野です。
ショットノイズとは
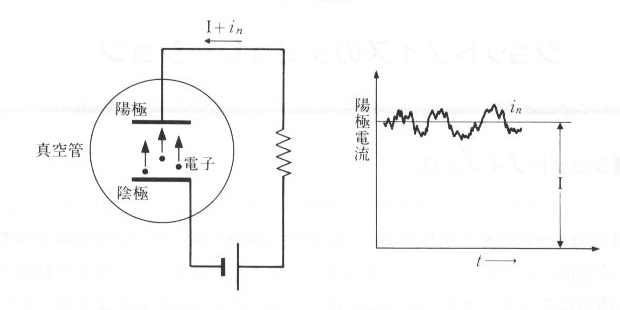
ショットノイズは真空管から発生する雑音です。真空管は、図7.1.1のように、陰極と陽極があり、陰極から陽極へ電子が飛ぶことにより、電流が流れ、
間にある網状の金属(グリッド)に電位をかけることにより、この電流を制御する構造になっています。電流は連続的に流れるように思われますが、電子という”つぶつぶなも
の”が、移動するため、詳細に観察すると、陰極から電子が不規則に放出しているので、電流が I+in のように変動します。この陽極電流の動揺成分 in をショットノイズといいます。このノイズは次のようのなメカニズムにより発生すると考えられます。陰極から陽極にむかって電子1個が放出されると、そ
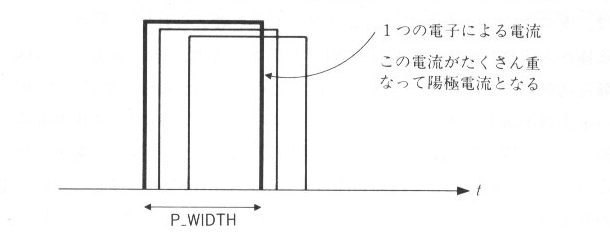
の瞬間から、陽極へ靜電誘導によって、回路に電流が流れ始め、電子が陽極へ到達したあと、この電流は、消滅します。図7.1.2のように、このパルス状の
電流が存続している間に、次々と多くの電子が到達するので、その結果として、陽極電流が連続したものになります。この際、電 子の発生はランダムですから、陽極電流が動揺することになるのです。
| 図7.1.1 ショットノイズ |
 |
| 図7.1.2 拡大した陽極電流 |
 |
ショットノイズのシミュレーション
プログラムs0710.cは、ショットノイズを、シミュレーションするプログラムです。電子1個による電流は、急竣なパルス状と仮定します。すなわち、幅 P_WIDTH 、高さ1の矩形パルスとします。電子は、3.2節で学んだポアソン分布により発生すると考えられ、単位時間に P=0.1 という小さい確率とします。行34 の for ループは、時刻を1づつ進めており、そのたびに 行35のように、 P という確率で電子が飛び出します。その時、幅 P_WIDTH の時間にわたって、 i[tt] という配列に1を加え、それが電子1個による電流波形になるわけです。 T_END になるまで、シミュレーションを続けます。
つぎにこの電流波形を図示しますが、その前に 行44によりヒストグラムを作成し、また平均値、分散の計算をしておきます(注)。このとき、時刻が 0 から P_WIDTH までの間は過渡状態ですから、計算からのぞきます。
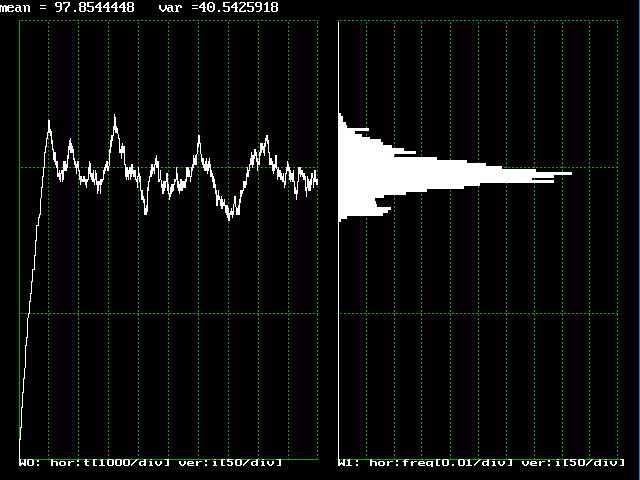
図7.1.3がシミュレーションの結果です。ウインドウ0に電流波形を、ウインドウ1に電流の分布を示します。この図でわかるように、ショットノイズは、歩幅1、歩く時間が不定のランダムウオークに相当し、その分布は正規分布をしていることがわかります。
| 図7.1.3 ショットノイズのシミュレーション結果 |
 |
| s0710.c ショットノイズのシミュレーション |
/* s0710.c
* ショットノイズのシミュレーション
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h> /* printf() */
#include "compati.h"
#include "window.h"
#define T_END 10000
#define P 0.1
#define P_WIDTH 1000
long t,tt;
int i[T_END] = {0}; /* 電流 */
long f[150] = {0}; /* ヒストグラム */
double x = 0.0;
double x2 = 0.0;
long n = 0;
long ii,j;
int main(void)
{
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,(double)T_END,150.0,SPACE,HIGHT-SPACE,WIDTH/2,SPACE);
Axis(0, "t", T_END / 10, "i", 50);
MoveTo(0, 0.0, 0.0);
SetWindow(1, 0.0,0.0,0.1,150.0,WIDTH/2+SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(1, "freq", 0.01, "i", 50);
/* メイン */
srand(5);
for (t = 0; t < T_END; t ++) {
if (P > RAND()) {
for (tt = t; tt <= t+P_WIDTH; tt ++) {
if (tt < T_END) {
i[tt] = i[tt] + 1 ;
}
}
}
}
for (t = P_WIDTH; t < T_END; t ++) {
f[i[t]] = f[i[t]] + 1;
x = x + (double)i[t];
x2 = x2 + (double)i[t] * (double)i[t];
n = n + 1;
}
/* 表示 */
printf("mean = %f8 var =%f8 \n",
x / (double)n, (x2 - x * x / (double)n) / (double)n);
for (t = 0; t < T_END; t ++) {
LineTo(0, (double)t, (double)(i[t]));
}
setlinestyle(0, 0, 3);
for (ii = 0; ii < 150; ii ++) {
Line(1, 0.0, (double)ii, (double)f[ii] / (double)n, (double)ii);
}
getch();
closegraph();
return 0;
}
|
ガウス雑音
前節でのべた真空管の陽極電流は、直流分に正規分布の雑音(これをガウス雑音という)が重量したものでした。このほかに雑音には、熱雑音というものがあ
ります。熱雑音は抵抗から発する雑音で、これも正規分布となります。それは、電流は非常に多数の電子が作る微小電流を合成したもので、それぞれが抵抗の中
で、不規則な熱運動をするため、抵抗の両端に、正規分布の雑音電圧が発生するのです。
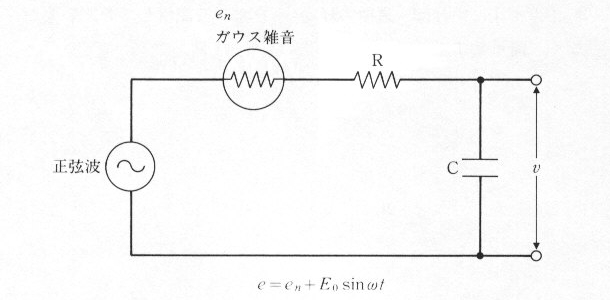
今、正弦波とこのガウス雑音が重量された波形を、図7.2.1のようにコンデンサCと抵抗RのCRローパスフィルタに加えると、どのような波形が得られるか、シミュレーションしてみることにしましょう。
ガウス雑音は、4.5節でのべた正規乱数の関数を用いて作ることができます。
| 図7.2.1 CRフィルタ |
 |
CRフィルタ
図7.2.1において次の微分方程式が成立します。
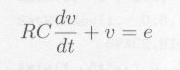 |
・・・・・ |
式7.2.1 |
すなわち
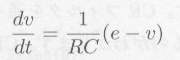 |
・・・・・ |
式7.2.2 |
この微分方程式を解くには、ルンゲクッタ法を用います(注)。
プログラムs0720.cにおいて、関数
double noise(double en);
は、熱雑音電圧 en のガウス雑音を発生させます。また、
double cr(double e, double v);
は式7.2.2を表わしています。行43から行47までで、ルンゲクッタ法により、微分方程式を解いています。
アウトプット
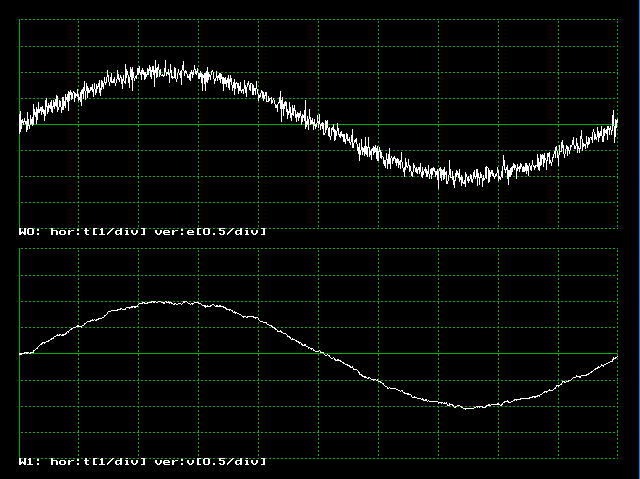
2つのウィンドを用い、ウインドウ0には、正弦波と雑音波の合計を表示し、ウインドウ1にフィルタの出力 v を表示しています。図7.2.2のように、CRフィルタを通った波形は、こまかい雑音が少なく、スムースになっているのがわかります。CRフィルタは典型的なローパスフィルタで、雑音を減らす効果があります。
| 図7.2.2 CRフィルタのシミュレーション結果 |
 |
| s0720.c CRフィルタのシミュレーション |
/* s0720.c
* CRフィルタのシミュレーション
* (C) H.Ishikawa 1994 2018
*/
#include <math.h> /* sin() */
#include "compati.h"
#include "window.h"
#define C 1.0
#define R 0.1
#define E0 1.0 /* 信号の振幅 */
#define OMEGA 2.0*3.141592*0.1 /* 信号の角周波数 */
#define E_NOISE 0.1 /* 雑音の標準偏差 */
#define T_END 10.0 /* シミュレーションの終了 */
#define DT 0.01 /* シミュレーションのきざみ */
double noise(double en);
double cr(double e, double q);
int main(void)
{
double e ,v ;
double t;
double k1,k2,k3,k4;
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "t", 1.0, "e", 0.5);
SetWindow(1, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "t", 1.0, "v", 0.5);
MoveTo(0, 0.0, 0.0);
MoveTo(1, 0.0, 0.0);
/* メイン */
srand(5);
v = 0.0;
for (t = 0.0; t <= T_END; t = t+DT) {
e = noise(E_NOISE) + E0 * sin(OMEGA * t);
k1 = DT * cr(e, v);
k2 = DT * cr(e, v + k1 / 2.0);
k3 = DT * cr(e, v + k2 / 2.0);
k4 = DT * cr(e, v + k3);
v = v + (k1 + 2.0 * k2 + 2.0 * k3 + k4) / 6.0;
LineTo(0, t, e);
LineTo(1, t, v);
}
getch();
closegraph();
return 0;
}
double cr(double e, double v)
{
return((e - v) / (C * R));
}
double noise(double en)
{
double xw = 0.0;
int i;
for (i = 1; i <= 12; i ++){
xw = xw + RAND();
}
return(en * (xw - 6.0));
}
|
移動平均
前節と同様の正弦波と熱雑音が重量された波形を、こんどは移動平均という方法で処理し、信号を分離することを試みましょう。
移動平均は、統計手法としてよく用いられる方法で、振幅の変化の激しい時系列について、その中の細かい変化を無視し、その大勢をわかりやすくするもので す。具体的には、ある測定値を中心として、その前後の一定の個数( M )を平均して、その平均化されたものを移動平均といいます。すなわち、図7.3.1のように、x1
, x2, ・・・xi の移動平均 ui は、
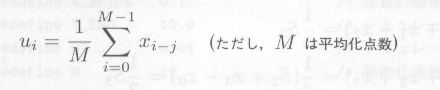 |
・・・・・ |
式7.3.1 |
となります。
| 図7.3.1 移動平均 |
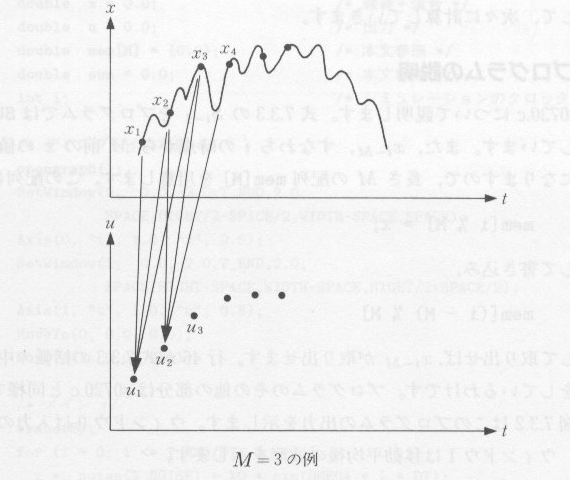 |
たとえば、 M=3 の場合、移動平均 ui は
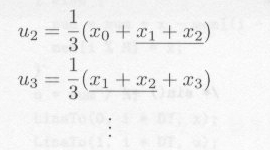 |
・・・・・ |
式7.3.2 |
となり、下線部分に同じ計算が入っています。平均化点数が小さいときには、問題がないのですが、この点数が大きくなると時間ロスが大きくなるので、
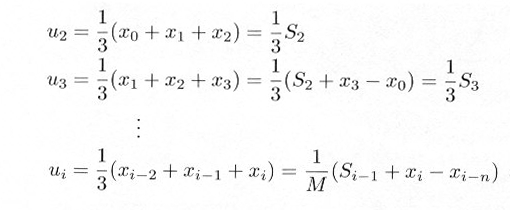 |
・・・・・ |
式7.3.3 |
として、つぎつぎに計算していきます。
プログラムの説明
プログラムs0730.cについて説明します。式7.3.3の Si-1 をプログラムでは sum と表わしています。また、 xi-M すなわち、 i の時点から M 前の x の値が必要になりますので、長さ M の配列 mem[M] を用意します。この配列に
mem[i % M] = x;
として書き込み
mem[(i - M) % M]
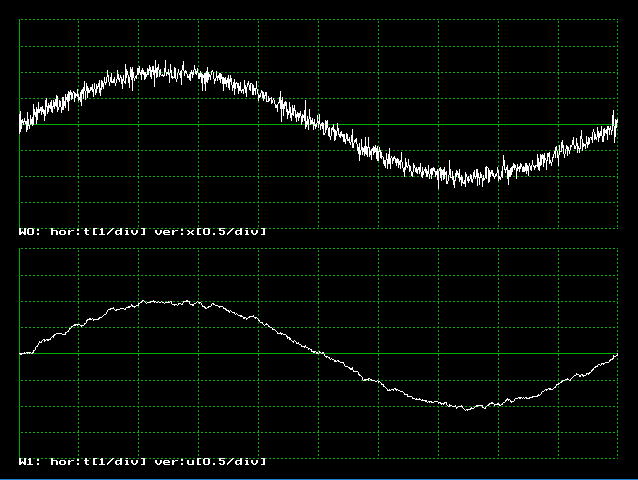
として取り出せば、 xi-M が取り出せます。行46が式7.3.3のかっこの中の計算をしているわけです。プログラムのそのほかの部分はプログラムs0720.cと同様です。出力は、図7.3.2のように、ウインドウ0は入力の波形を、ウインドウ1で、移動平均後の波形を示します。
| 図7.3.2 移動平均による信号の分離 |
 |
| s0730.c 移動平均による信号の分離 |
/* s0730.c
* 移動平均による信号の分離
* (C) H.Ishikawa 1994 2018
*/
#include <math.h> /* sin() */
#include "compati.h"
#include "window.h"
#define X0 1.0 /* 信号の振幅 */
#define OMEGA 2.0*3.141592*0.1 /* 信号の角周波数 */
#define X_NOISE 0.1 /* 雑音の標準偏差 */
#define T_END 10.0 /* シミュレーションの終了 */
#define DT 0.01 /* シミュレーションのきざみ */
#define M 11 /* 平均化点数 */
double noise(double xn);
int main(void)
{
double x = 0.0; /* 雑音+信号 */
double u = 0.0; /* 出力 */
double mem[M] = {0.0}; /* 本文参照 */
double sum = 0.0; /* 本文参照 */
int i; /* シミュレーションのクロック */
/* ディスプレイの準備 */
opengraph();
SetWindow(0, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "t", 1.0, "x", 0.5);
SetWindow(1, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "t", 1.0, "u", 0.5);
MoveTo(0, 0.0, 0.0);
MoveTo(1, 0.0, 0.0);
/* メイン */
srand(5);
for (i = 0; i <= T_END/DT; i ++) {
x = noise(X_NOISE) + X0 * sin(OMEGA * i * DT);
if (i < M) { /* 0からM-1までの始めの部分 */
sum = sum + x;
mem[i] = x;
} else { /* M以上の場合 */
sum = sum + x - mem[(i - M) % M];
mem[i % M] = x;
}
u = sum / M;
LineTo(0, i * DT, x);
LineTo(1, i * DT, u);
}
getch();
closegraph();
return 0;
}
double noise(double xn)
{
double xw = 0.0;
int i;
for (i = 1; i <= 12; i ++){
xw = xw + RAND();
}
return(xn * (xw - 6.0));
}
|
雑音にうもれた信号を取り出す
雑音の方が信号より大きいという悪条件の中で、信号を取り出すにはどうしたらいいのでしょうか。もしも同じ信号が、くり返し発せられるということが、わ
かっていれば、図7.4.1のように波形を加算し、平均することにより、雑音の影響を少なくすることができます。ただし信号を時系列上で同じ位置に固定し
て加算しなけれはいけません。これを信号と同期をとるといい、同期加算とよばれるゆえんです。アンサンブル平均ともいいます。
| 図7.4.1 同期加算の原理 |
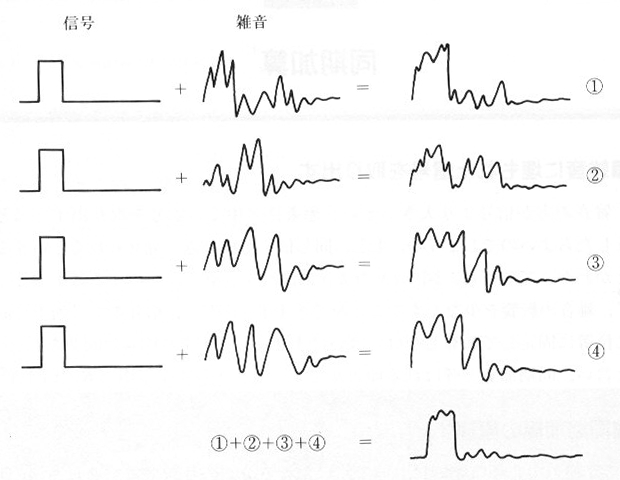 |
同期加算の原理
3.5節の中心極限定理において、いかなる分布の乱数でも、それを m 回加算したあとの分布を見ると、もとの乱数の分散を σ2 とすると、分散が mσ2 の正規乱数に近づくということを知りました。すなわち、標準偏差で言うと、
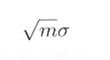
になるということです。このことは加算したあと加算回数で割ると(すなわち平均をとると)、標準偏差は
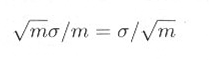
となり m 回の加算で、標準偏差が
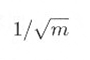
になることになります。ガウス雑音の平均振幅は標準偏差であらわされますから、ガウス雑音をつぎつぎ m 回加算して平均をとると、その大きさは
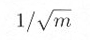
になるはずです。一方、信号の方は、タイミングをあわせて、(同期して)加算されるので、その平均振幅は変わりません。したがって、信号と雑音の比(S/N比とよばれる)は、加算回数にしたがって、改善されていきます。これが同期加算の原理です。
シミュレーションプログラム
プログラムs0740.cにより、同期加算をシミュレーションしてみましょう。信号は関数
doube signal(double t, double peak, double p_width);
により発生させます。これは高さ peak 、幅 p_width の単パルスです。雑音は例によってガウス雑音を
double noise (double sd);
により、正規乱数として発生させます。信号と雑音の合計を x とし、各クロック i ごとにそれを配列 mem[i] に加えて平均を計算していきます。
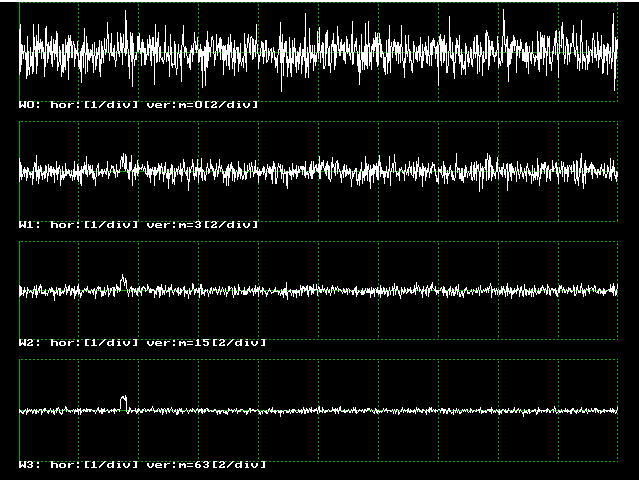
ディスプレイ上には、4つのウインドウ(ウインドウ番号 j=0, 1, 2, 3 )を用意し、それぞれに加算回数 0, 3, 15, 63に対応させ、その回数に達したそきに表示させることとします。
| s0740.c 同期加算による信号の分離 |
/* s0740.c
* 同期加算による信号の分離
* (C) H.Ishikawa 1994 2018
*/
#include "compati.h"
#include "window.h"
#define X0 0.5 /* 信号のピーク値 */
#define W 0.1 /* 信号の幅 */
#define NOISE 0.50 /* 雑音の標準偏差 */
#define T_END 10.0 /* シミュレーションの終了時刻 */
#define DT 0.01 /* シミュレーションのキザミ */
#define M 1000 /* memの大きさ T_END/DT */
#define N 4 /* 加算回数が0,3,15,63のときに表示 */
#define N_END 64 /* 加算回数の最大 */
double signal(double t, double peak, double width);
double noise(double sd);
int main(void)
{
int m; /* 加算回数 */
int mm = 1; /* 表示する加算回数 */
int j = 0; /* 表示するウィンドの番号 */
double x = 0.0; /* 信号+雑音 */
double mem[M] = {0.0};/**/
int i;
/* ディスプレイの準備 */
opengraph();
SetWindow(0, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/4-SPACE,WIDTH-SPACE,0);
Axis(0, "", 1.0, "m=0", 2.0);
MoveTo(0, 0.0, 0.0);
SetWindow(1, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/2-SPACE,WIDTH-SPACE,HIGHT/4);
Axis(1, "", 1.0, "m=3", 2.0);
MoveTo(1, 0.0, 0.0);
SetWindow(2, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/4*3-SPACE,WIDTH-SPACE,HIGHT/2);
Axis(2, "", 1.0, "m=15", 2.0);
MoveTo(2, 0.0, 0.0);
SetWindow(3, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/4*3);
Axis(3, "", 1.0, "m=63", 2.0);
MoveTo(3, 0.0, 0.0);
/* メイン */
srand(5);
for (m = 0; m <= N_END; m ++) {
for (i = 0; i < T_END / DT; i ++) {
x = noise(NOISE) + signal(i * DT, X0, W);
mem[i] = (mem[i] * m + x) / (m + 1);
}
if (m == mm - 1) {
for (i = 0; i < T_END / DT; i ++) {
LineTo(j, i * DT, mem[i]); /* jのウィンドウに表示 */
}
mm = mm * N;
j = j + 1;
}
}
getch();
closegraph();
return 0;
}
double signal(double t, double peak, double width)
{
double t0 = 1.7; /* パルスの始まり時刻 */
if (t0 <= t && t <= t0 + width) {
return(peak);
} else {
return(0.0);
}
}
double noise(double sd)
{
double xw = 0.0;
long i;
for (i = 1; i <= 12; i ++){
xw = xw + RAND();
}
return(sd * (xw - 6.0));
}
|
実行結果
プログラムs0740.cを実行してみましょう。信号の振幅 0.5 に対して、雑音の大きさが同じ標準偏差 0.5 として計算しています。原波形(ウインドウ0)において、信号はどこにあるのかまったくわかりません。それが、加算回数を増やして行くと、信号がうかびあ
がってくるのがわかります.加算回数63回では、十分に信号を認識することができます。
| 図7.4.2 同期加算による信号の分離 |
 |
1. ショットノイズは、歩幅1、歩く時間が不定のランダムウオークであることに、注意しなさい。(6章演習2.参照)
(解答省略)
2. s0730.cにおいては、平均化点数を11としていました。さまざまな平均化点数を用いてシミュレーションをおこない、出力波形を観測しなさい。
(解答省略)
3. 雑音にうもれた正絃波を、同期加算により、分離しなさい。
(解答)
| a0730.c 7章3.の解答 同期加算による正弦波信号の分離 |
/* a0730.c 7章3.の解答
* 同期加算による正弦波信号の分離
* (C) H.Ishikawa 1994 2018
*/
#include <math.h>
#include "compati.h"
#include "window.h"
#define X0 0.3 /* 信号の振幅 */
#define OMEGA 2.0*3.141592*2.0 /* 信号の角周波数 */
#define NOISE 0.50 /* 雑音の標準偏差 */
#define T_END 10.0 /* シミュレーションの終了時刻 */
#define DT 0.01 /* シミュレーションのキザミ */
#define M 1000 /* memの大きさ T_END/DT */
#define N 4 /* 加算回数が0,3,15,63のときに表示 */
#define N_END 64 /* 加算回数の最大 */
double signal(double t, double peak, double width);
double noise(double sd);
int main(void)
{
int m; /* 加算回数 */
int mm = 1; /* 表示する加算回数 */
int j = 0; /* 表示するウィンドの番号 */
double x = 0.0; /* 信号+雑音 */
double mem[M] = {0.0};/**/
int i;
/* ディスプレイの準備 */
opengraph();
SetWindow(0, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/4-SPACE,WIDTH-SPACE,0);
Axis(0, "", 1.0, "m=0", 2.0);
MoveTo(0, 0.0, 0.0);
SetWindow(1, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/2-SPACE,WIDTH-SPACE,HIGHT/4);
Axis(1, "", 1.0, "m=3", 2.0);
MoveTo(1, 0.0, 0.0);
SetWindow(2, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/4*3-SPACE,WIDTH-SPACE,HIGHT/2);
Axis(2, "", 1.0, "m=15", 2.0);
MoveTo(2, 0.0, 0.0);
SetWindow(3, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/4*3);
Axis(3, "", 1.0, "m=63", 2.0);
MoveTo(3, 0.0, 0.0);
/* メイン */
srand(5);
for (m = 0; m <= N_END; m ++) {
for (i = 0; i < T_END / DT; i ++) {
x = noise(NOISE) + X0 * sin(OMEGA * i * DT);
mem[i] = (mem[i] * m + x) / (m + 1);
}
if (m == mm - 1) {
for (i = 0; i < T_END / DT; i ++) {
LineTo(j, i * DT, mem[i]); /* jのウィンドウに表示 */
}
mm = mm * N;
j = j + 1;
}
}
getch();
closegraph();
return 0;
}
double signal(double t, double peak, double width)
{
double t0 = 1.7; /* パルスの始まり時刻 */
if (t0 <= t && t <= t0 + width) {
return(peak);
} else {
return(0.0);
}
}
double noise(double sd)
{
double xw = 0.0;
long i;
for (i = 1; i <= 12; i ++){
xw = xw + RAND();
}
return(sd * (xw - 6.0));
}
/* a0730.c 7章3.の解答
* 同期加算による正弦波信号の分離
* (C) H.Ishikawa 1994 2018
*/
#include <math.h>
#include "compati.h"
#include "window.h"
#define X0 0.3 /* 信号の振幅 */
#define OMEGA 2.0*3.141592*2.0 /* 信号の角周波数 */
#define NOISE 0.50 /* 雑音の標準偏差 */
#define T_END 10.0 /* シミュレーションの終了時刻 */
#define DT 0.01 /* シミュレーションのキザミ */
#define M 1000 /* memの大きさ T_END/DT */
#define N 4 /* 加算回数が0,3,15,63のときに表示 */
#define N_END 64 /* 加算回数の最大 */
double signal(double t, double peak, double width);
double noise(double sd);
int main(void)
{
int m; /* 加算回数 */
int mm = 1; /* 表示する加算回数 */
int j = 0; /* 表示するウィンドの番号 */
double x = 0.0; /* 信号+雑音 */
double mem[M] = {0.0};/**/
int i;
/* ディスプレイの準備 */
opengraph();
SetWindow(0, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/4-SPACE,WIDTH-SPACE,0);
Axis(0, "", 1.0, "m=0", 2.0);
MoveTo(0, 0.0, 0.0);
SetWindow(1, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/2-SPACE,WIDTH-SPACE,HIGHT/4);
Axis(1, "", 1.0, "m=3", 2.0);
MoveTo(1, 0.0, 0.0);
SetWindow(2, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT/4*3-SPACE,WIDTH-SPACE,HIGHT/2);
Axis(2, "", 1.0, "m=15", 2.0);
MoveTo(2, 0.0, 0.0);
SetWindow(3, 0.0,-2.0,T_END,2.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/4*3);
Axis(3, "", 1.0, "m=63", 2.0);
MoveTo(3, 0.0, 0.0);
/* メイン */
srand(5);
for (m = 0; m <= N_END; m ++) {
for (i = 0; i < T_END / DT; i ++) {
x = noise(NOISE) + X0 * sin(OMEGA * i * DT);
mem[i] = (mem[i] * m + x) / (m + 1);
}
if (m == mm - 1) {
for (i = 0; i < T_END / DT; i ++) {
LineTo(j, i * DT, mem[i]); /* jのウィンドウに表示 */
}
mm = mm * N;
j = j + 1;
}
}
getch();
closegraph();
return 0;
}
double signal(double t, double peak, double width)
{
double t0 = 1.7; /* パルスの始まり時刻 */
if (t0 <= t && t <= t0 + width) {
return(peak);
} else {
return(0.0);
}
}
double noise(double sd)
{
double xw = 0.0;
long i;
for (i = 1; i <= 12; i ++){
xw = xw + RAND();
}
return(sd * (xw - 6.0));
}
|
|
 |
