モンテカルロシミュレーション

5.1 ビュホンの針
5.2 数値積分
5.3 多重積分
演習

５．　乱数を用いた実験数学－－モンテカルロ法－－

　本章では、モンテカルロ法とよばれる、乱数を用いて問題を解く方法を学びます。解析的に計算が困難な問題でも、制限なく解くことができます。１桁精度をあげるために、それまで要した計算の１００倍の時間がかかり、実行時間が遅いのが欠点です。

平行線と針の交わる確率
　１８世紀のフランスの自然科学者 Comte de Buffonは、πの近似値を次のような実験で求めました。まず、平面上に平行線を何本か引き、その間隔と同じ長さの針をその上に落とします。針はランダムに落ち、平行線と交わるものと、そうでないものがあります。針の交わる確率が、2/πとなることから、落とした針の本数と、交わった針の本数の比とから、πを求めようとするものです。

図５．１．１　ビュフォンの針

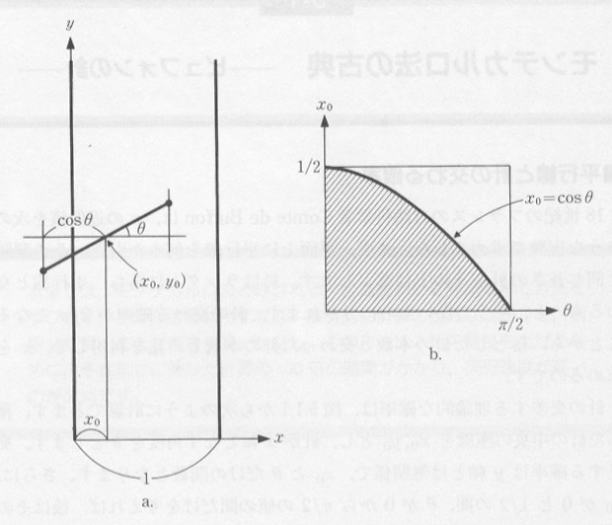　針の交差する理論的な確率は、図５．１．１から次のように計算できます。落ちた針の中央の座標を x₀, y₀ とし、針が x 軸となす角度を θ とします。交差する確率は y 軸とは無関係で、 x₀ と θ だけの関数となります。さらに、 x₀ が 0 と 1/2 の間、 θ が 0 から π/2 の値の間だけを考えれば、あとはその繰り返しになります。
　平行線と交わるための条件は、図５．１．１ａから x₀≦cosθ となりますから、図５．１．１ｂの cosθ の下側であれば交わることとなります。この斜線部分の面積（ =1/2 ）と長方形の面積（ =π/4 ）との比が、交差する確率となります。すなわち
　交差する確率 =2/π
となります。何本も針を落として見て、交わっている針の数をかぞえ、その確率がもとめられたとします。その確率からこの式に従ってπを求めようとするものです。

シミュレーションで再現するビュフォンの針
　プログラムs0510.cは、シミュレーションで針を落とす実験を再現したもので、ディスプレイ画面の上に９本の平行線を引き、そこに針を落とす様子が次々に表示されます。プログラムの中の行44は針の先端の x 座標の整数部が異なっていることにより、平行線と交わっていることを検出しています。
　実行してみましょう。この結果、π　の値は3.14に近い数値が得られますか。（図５．１．２）

図５．１．２　ビュフォンの針　実行結果

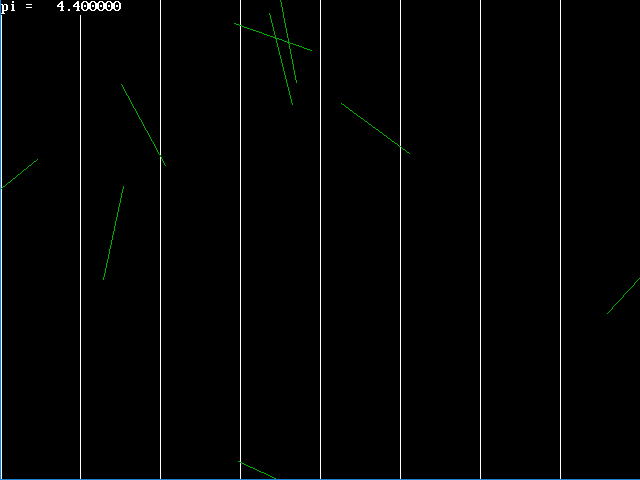１０本

１００本

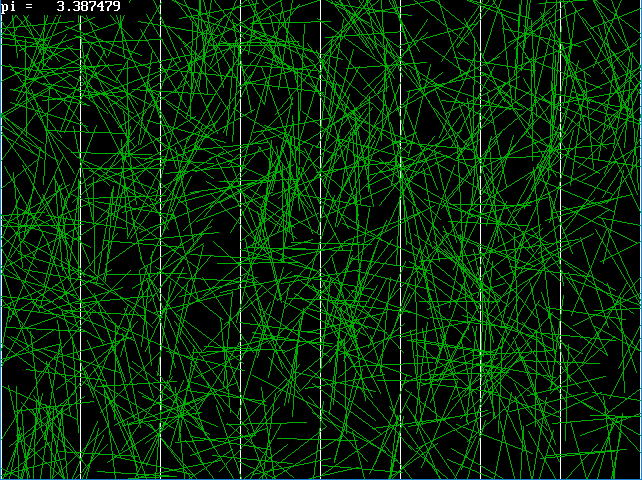１０００本

　 s0510.c　　　ビュフォンの針

/*  s0510.c 
 *         ビュフォンの針  
 *          (C) H.Ishikawa  1994  2018
 */

#include <stdio.h>            /* printf() */
#include <math.h>             /* sin(), cos() */
#include "compati.h"
#include "window.h"

#define NUMBER   1000         /* 落とした針の本数 */
#define X_MAX    8
#define Y_MAX    6
#define PI       3.1415927

int main(void)
{
  int    j;                   /* forのカウンタ */
  int    xl;                  /* forのカウンタ */
  int    n1 = 0;              /* 針が交わった回数 */
  double x0, y0;              /* 針の中央の座標 */
  double x1, y1, x2, y2;      /* 針の先端の座標 */
  double th;                  /* θ */

  /* グラフィックの準備 */
  opengraph();
  setcolor(15);
  SetWindow(0,  0, 0, X_MAX, Y_MAX, 0, HIGHT, WIDTH, 0);
  for (xl = 0; xl <= X_MAX; xl ++) {
    Line(0,  xl, 0, xl, Y_MAX);  /* 平行線 */
  }
  setcolor(2);                   /* 緑 */

  /* メイン */
  srand(3);
  for (j = 1; j <= NUMBER; j ++) {
    x0 = X_MAX * RAND();
    y0 = Y_MAX * RAND();
    th = 2 * PI * RAND();
    x1 = x0 + cos(th) / 2;
    y1 = y0 + sin(th) / 2;
    x2 = x0 - cos(th) / 2;
    y2 = y0 - sin(th) / 2;
    Line(0,  x1, y1, x2, y2);
    if ((int)x1 != (int)x2) {   /* 針の両端の座標の整数部が異なっている時 */
      n1 = n1 + 1;
    }
  }
  printf("pi = %10f \n", (double)j /n1 * 2);
  getch();
  closegraph();
  return 0;
}

５．２　乱数によりπを求めるもう１つの例－－モンテカルロ法による数値積分－－

大数の法則の応用
　ビュフォンの針は、特別な方法でπを求めましたが、もっとこれを一般化してみます。３．４節の大数の法則で述べたように、コイン投げを多数回（ m 回）試みると、成功の回数（ k ）との比は一定値に近づきます。モンテカルロ法は、コインを投げる代わりにある実験を行い、その成功の数を数える実験的な数学です。 π を求める計算をシミュレーション実験し、モンテカルロ法を理解しましょう。

正方形の上に雨が降る
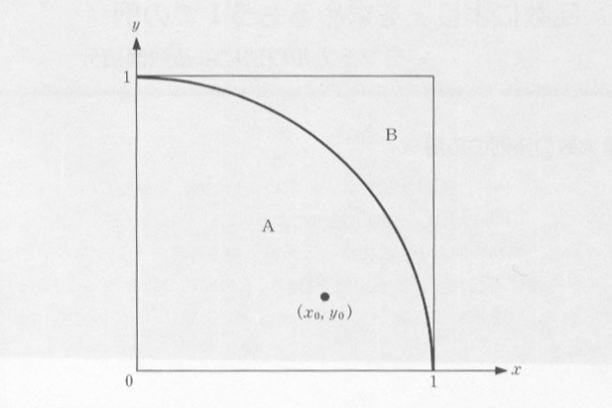
　図５．２．１のように、半径１の１／４円を、一辺が１の正方形に接するように書くとしましょう。この正方形を、雨の降る中にさらしたとします。雨滴は均一に、ランダムに降りそそぎますから、１／４円の内側（図のＡの部分）も、残りの部分（図のＢの部分）もぬらします。Ａの部分に落ちる雨滴の数と、正方形の雨滴の数の比は、大数の法則により面積の比に近づくはずです。すなわち、

・・・・・

式5.2.1

となります。ここで、　右辺は、π／４ですから、もし雨滴の数を数えることができれば、

・・・・・

式5.5.2

として、πが計算できるはずです。

図5.2.1　１／４円

プログラムのポイント
　RAND()マクロにより、区間 [0, 1) の乱数を２個発生し、それぞれを x₀, y₀ とします。もし

・・・・・

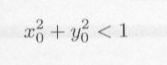式5.2.3

ならば、Ａの部分の雨滴に相当します。多数（ j 個）の乱数を発生させ、Ａにある回数 k を数え、

・・・・・

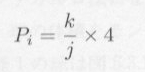式5.2.4

としてπを求めます。
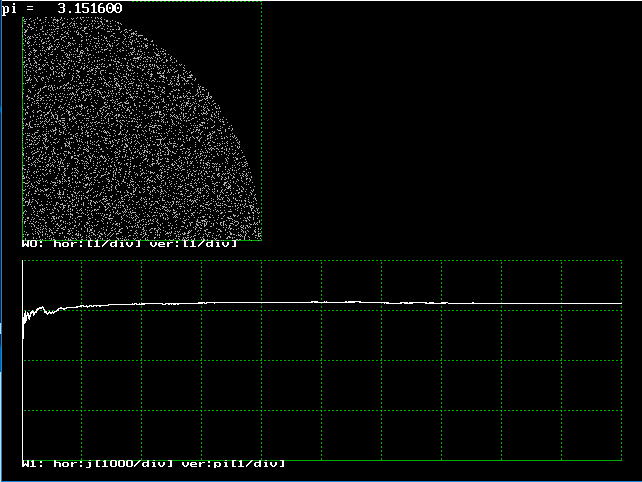
　プログラムs0520.cは、雨滴が正方形をぬらしていくありさまをディスプレイするようにしたものです。図５．２．２のように j が大きくなるにつれて、 π に収束していくことがわかります。

図５．２．２　モンテカルロ法によるπの計算結果

　 s0520.c 　　モンテカルロ法によるπ

/*  s0520.c
 *         モンテカルロ法によるπ  
 *          (C) H.Ishikawa 1994 2018
 */

#include <stdio.h>                  /* printf() */
#include "compati.h"
#include "window.h"
#define NUMBER   10000              /* 雨滴の合計 */

int main(void)
{
  int    j;                         /* forのカウンタ */
  int    n1 = 0;                    /* 円の中に入った雨滴 */
  double x0, y0;                    /* 雨滴の座標 */
  double pi;                        /* πの近似値 */

  /*グラフィックの準備*/
  opengraph();
  SetWindow(0,  0, 0, 1, 1, SPACE, HIGHT/2, HIGHT/2 + SPACE, 0);
  Axis(0, "", 1,"", 1);
  SetWindow(1,  0, 0, NUMBER, 4, 
            SPACE, HIGHT-SPACE, WIDTH-SPACE, HIGHT/2+SPACE);
  Axis(1, "j", NUMBER / 10, "pi",1);
  MoveTo(1, 0, 0);sleep(1);

  /*メイン*/
  srand(3);
  for (j = 1; j <= NUMBER; j ++) {
    x0 = RAND();
    y0 = RAND();
    if (x0 * x0 + y0 * y0 < 1.0) {  /* 円の中に入った場合 */
      n1 = n1 + 1;
      PutPixel(0,  x0, y0, 7);
    }
    pi = (double)n1 / j * 4;
    LineTo(1, j, pi);
  }
  printf("pi = %10f \n", pi);
  getch();
  closegraph();
  return 0;
}

５．３　乱数により球の体積を求める－－モンテカルロ法による多重積分－－

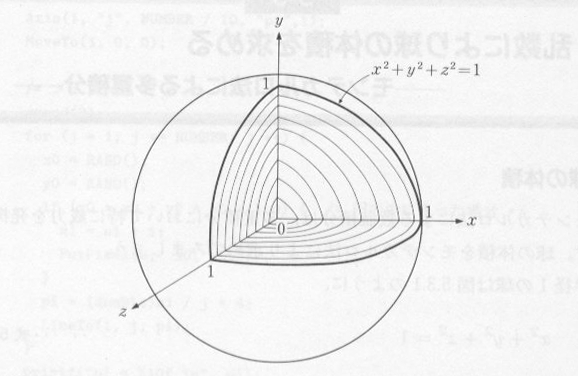
球の体積

　モンテカルロ法による数値積分は、多重積分において、特に威力を発揮します。球の体積をモンテカルロ法により求めてみましょう。　半径１の球は、図５．３．１のように、

・・・・・

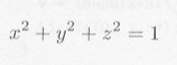式5.3.1

で表わされます。この球の体積 V は、図５．３．１の x-y 平面、 y-z 平面、 z-x 平面で切りとられる体積の８倍ですから、

・・・・・

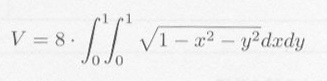式5.3.2

という定積分を行うこととなります。

図５．３．１　球

プログラムのポイント
　５．２の場合と同様に考え、RAND()マクロにより、区間 [0, 1) の一様乱数を３個発生させ、それぞれを、 x0 , y0 , z0 とします。もし、
　　x0 * x0 + y0 * y0 + z0 * z0 < 1
であれば、球の内側の乱数であったので、その数を数えます。全乱数の数 j と、内側であった数 k との比から、体積 V は、
　　v = 8 * k / j
として求めます。
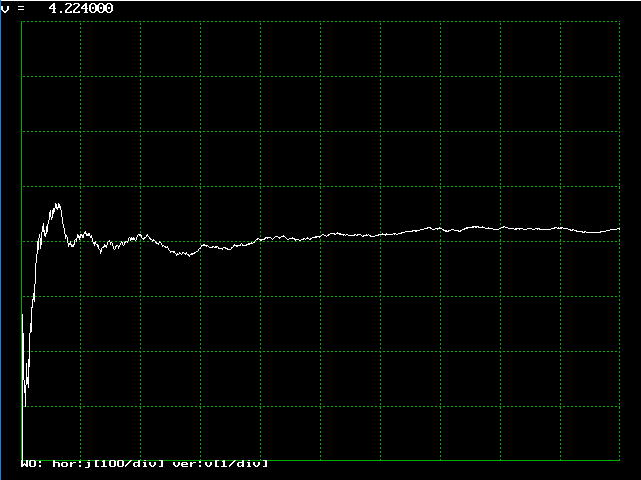
　プログラムs0530.cは球の体質を、モンテカルロ法により求めるプログラムです。
　実行し、理論値４／３・π（約4.19）と比較しましょう。

図５．３．２　モンテカルロ法による球の体積計算結果

　 s0530.c 　モンテカルロ法による球の体積

/*  s0530.c  
 *         モンテカルロ法による球の体積  
 *          (C) H.Ishikawa 1994 2018
 */

#include <stdio.h>                     /* printf() */
#include "compati.h"
#include "window.h"

#define NUMBER   1000                  /* 乱数の組の数 */

int main(void)
{
  int    j;                            /* forのカウンタ */
  int    n1 = 0;                       /* 球の中に入った数 */
  double x0, y0, z0;                   /* 点の座標 */
  double v;                            /* 体積の近似値 */

  /*グラフィックの準備*/
  opengraph();
  SetWindow(0,  0, 0, NUMBER, 8, 
            SPACE, HIGHT-SPACE, WIDTH-SPACE, SPACE);
  Axis(0, "j", NUMBER / 10, "v", 1);
  MoveTo(0, 0, 0);
  setlinestyle(0, 0, 2);

  /*メイン*/
  srand(3);
  for (j = 1; j <= NUMBER; j ++) {
    x0 = RAND();
    y0 = RAND();
    z0 = RAND();
    if (x0 * x0 + y0 * y0 + z0 * z0 < 1.0) {  /* 球の中に入った場合 */
      n1 = n1 + 1;
    }
    v = (double)n1 / j * 8;
    LineTo(0, j, v);
  }
  printf("v = %10f \n",v);
  getch();
  closegraph();
  return 0;
}

演習

１．　モンテカルロ法により、

を求めなさい（理論値 =1 - e^-1 = 0.632121 ）。
　　（解答）　　

　 a0510.c ５章１．解答　　 exp 定積分

/*  a0510.c  ５章１．解答
 *    　　     exp 定積分
 *          (C) H.Ishikawa 1994 2018
 */
#include <math.h>
#include <stdio.h>
#include "compati.h"

#define NUMBER   10000

int main(void)
{
  int    j;
  int    n1 = 0;
  double x0, y0;
  double s;

  srand(3);
  for (j = 1; j <= NUMBER; j ++) {
    x0 = RAND();
    y0 = RAND();
    if (y0 < exp(-x0)) {
      n1 = n1 + 1;
    }
  }
  s = (double)n1 / NUMBER;
  printf("s = %1.6f \n", s);
  return 0;
}

２．

という定積分を行うとき、区間 [0, 1) の乱数 r_i を用い、それを f(x) に次々代入し、

としても求められます。この方法により、１．と同じ定積分をもとめなさい。

　　（解答）　

　 a0520.c 　　５章２．解答　　exp 定積分その２

/*  a0520.c  ５章２．解答
 *         　　exp 定積分 その２
 *          (C) H.Ishikawa 1994 2018
 */
#include <math.h>
#include <stdio.h>
#include "compati.h"

#define NUMBER   10000

int main(void)
{
  int    j;
  double y0;
  double s = 0.0;

  srand(3);
  for (j = 1; j <= NUMBER; j ++) {
    y0 = exp(-RAND());
    s = s + y0;
  }
  s = s / NUMBER;
  printf("s = %1.6f \n", s);
  return 0;
}

３．　２．を拡張して

という多重積分を求めることができます。すなわち、３個１組の区間 [0, 1) の乱数 x₀, y₀, z₀ を n 組発生させ、

として求めます。この方法により、

を求めなさい。
　　（解答）

　 a0530.c 　　５章３．解答　　３重定積分

/*  a0530.c  ５章３．解答
 *         　　３重定積分
 *          (C) H.Ishikawa 1994 2018
 */
#include <stdio.h>
#include "compati.h"

#define NUMBER   10000

int main(void)
{
  int    j;
  double x0, y0, z0;
  double s = 0.0;

  srand(3);
  for (j = 1; j <= NUMBER; j ++) {
    x0 = RAND();
    y0 = RAND();
    z0 = RAND();
    s = s + 1.0 / ((0.01 + x0) + (0.02 + y0) + (0.03 + z0));
  }
  s = s / NUMBER;
  printf("s = %1.6f \n", s);
  return 0;
}