 |
|
4. どんな分布の乱数でも作り出せる−− 乱数の変換方法−−
|
第2章で,rand()関数から区間[0,1)の間の一様乱数を得るRAND()マクロを定義しました。システム・シミュレーションにおいては,一様乱数のみならず,さまざまな分布の乱数を用いることがあります。本章では,一様乱数からさまざまな分布の乱数を作り出す手法を学びます。
逆関数法
RAND()マクロで得られる乱数は、0と1の間、すなわち、区間 [0,1) ですが、それを区間 [a.b) のような特定区間の一様乱数を得るにはどうしたらよいのでしょうか。
一般に、区間 [0,1) の一様乱数から特定区間の一様乱数を得るには、次の逆関数法がよく使われます。
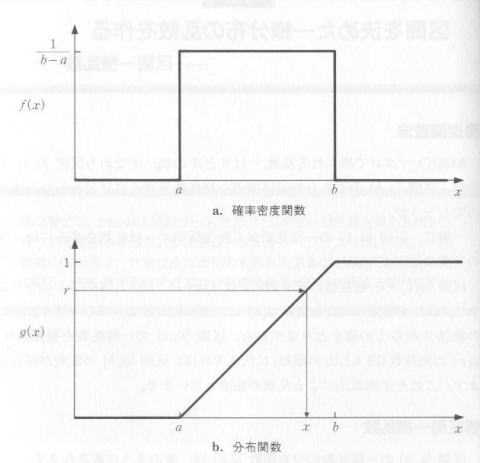
区間 [0,1) の一様乱数の確率密度関数 f(x) は、図4.1.1aのようになります(注)。
これを積分した分布関数 g(x) は図4.1.1bのようになります。 g(x) の値は0から1の値をとりますから、区間 [0,1) の一様乱数を
発生させ、 g(x) の逆関数(図4.1.1bの縦軸)に代入すれば、区間 [a,
b) の乱数が得られます。これを逆関数法による乱数の変換といいます。
| 図4.1.1 区間[a, b)の一様分布 |
 |
区間一様乱数
区間 [a, b) の一様乱数の分布関数 g(x) は次のように表わされます。
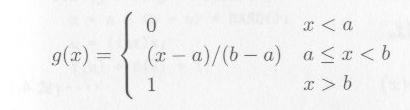 |
・・・・・ |
式4.1.1 |
x について解けば、
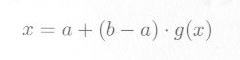 |
・・・・・ |
式4.1.2 |
となり、 g(x) のところにRANDマクロの [0, 1) の乱数を代入しますので、Cでは次のように表わせます。
x = a + (b - a) * RAND();
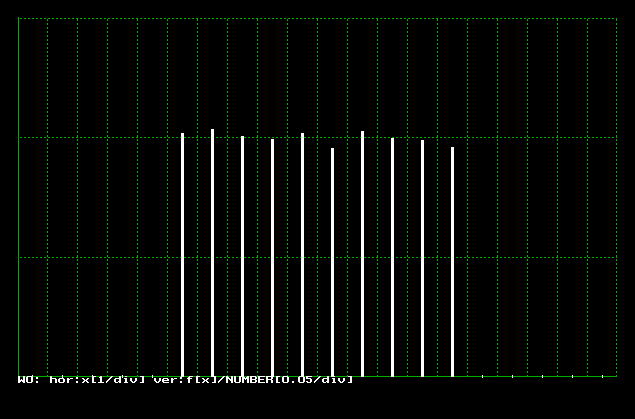
プログラムs0410.cの行29がこの式で,NUMBER個の区間[a, b)の一様乱数を発生させ,ヒストグラムに表示します。結果を図4.1.2に示します。
| s0410.c 区間一様乱数の発生 |
/* s0410.c
* 区間一様乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include "compati.h"
#include "window.h"
#define NUMBER 10000
#define SIZE 20 /* ヒストグラムの大きさ */
int main(void)
{
int j; /* forのカウンタ */
int u; /* xの整数部分 */
double x; /* 一様乱数n個の合計 */
double a = 5; /* 一様分布の下限 */
double b = 15; /* 一様分布の上限 */
int f[SIZE] = {0}; /* 頻度 */
/*グラフィックの準備*/
opengraph();
SetWindow(0, 0.0,0.0,20,0.1501, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "x",1, "f[x]/NUMBER", 0.050);
setlinestyle(0, 0, 3);
/*メイン*/
for (j = 0; j < NUMBER; j ++) {
x = a + (b - a) * RAND();
u = (int)x;
f[u] = f[u] + 1;
}
/*ヒストグラムの表示*/
for (u = 0; u < SIZE; u ++) {
Line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER);
}
getch();
closegraph();
return 0;
}
|
| 図4.1.2 区間一様乱数の発生結果 |
 |
逆関数法による指数乱数
3.3節で述べたとおり、ランダムに発生する事象の時間間隔を測ってみると、それは指数分布にしたがいます。8章以降で述べる、変化点方式と呼ばれるシミュレーションを行う場合、指数分布にしたがう乱数、すなわち指数乱数をよく用います。
指数分布の密度関数 f(τ) は、平均をλとすると、3.3節の式3.3.4のとおり、
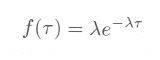 |
・・・・・ |
式4.2.1 |
であり(注)、分布関数 g(τ) は
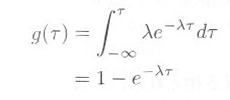 |
・・・・・ |
式4.2.2 |
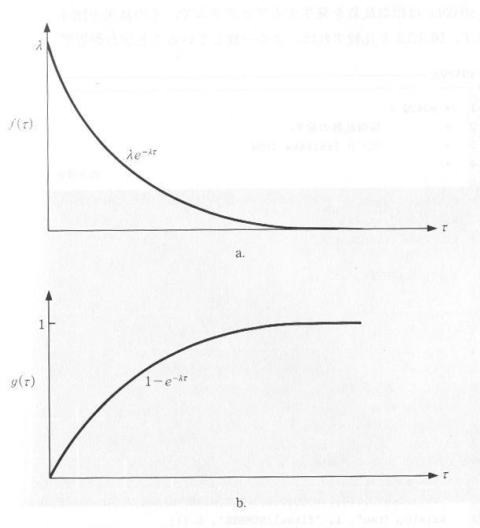
です。(図4.2.1参照)
| 図4.2.1 指数分布 |
 |
逆関数法で指数乱数を発生させるため、逆関数は、
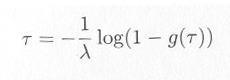 |
・・・・・ |
式4.2.3 |
となりますから,g(τ)をRAND()マクロに置き換えれば,τは指数乱数となります。Cでは,λをlambdaと表現すれば,
tau = -1.0 / lambda * (1.0 - RAND());
のようにかけます。
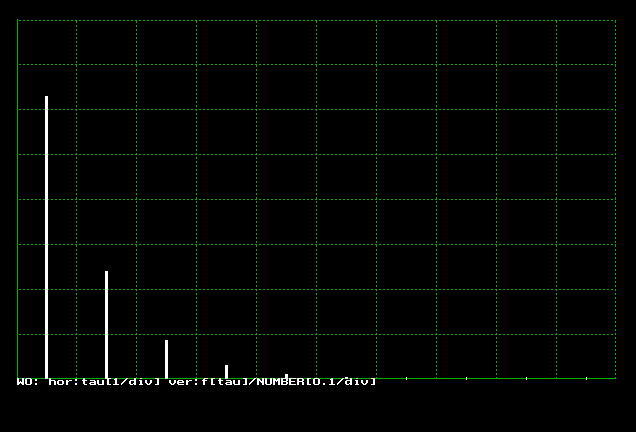
プログラムs0420.cは指数乱数を発生するプログラムで,その結果を図4.2.2に示します。図3.3.2と比較すれば,よく一致しています。
| s0420.c 指数乱数の発生 |
/* s0420.c
* 指数乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include <math.h> /* log() */
#include "compati.h"
#include "window.h"
#define NUMBER 10000
int main(void)
{
int j; /* forのカウンタ */
int u; /* τの整数部分 */
int f[100] = {0}; /* uの頻度 */
double tau; /* τ */
double lambda = 1; /* λ */
/*グラフィックの準備*/
opengraph();
SetWindow(0, 0.0,0.0,10,0.8, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "tau", 1, "f[tau]/NUMBER", 0.1);
setlinestyle(0, 0, 3);
/*メイン*/
srand(15);
for (j = 0; j <= NUMBER; j++) {
tau = -1.0 / lambda * log(1.0 - RAND());
u = (int)tau;
f[u] = f[u] + 1;
}
/*ヒストグラムの表示*/
for (u = 0; u < 15; u ++) {
Line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER);
}
getch();
closegraph();
return 0;
}
|
| 図4.2.2 指数乱数の発生結果 |
 |
指数乱数からポアソン乱数を作る
ポアソン乱数の発生は、指数乱数を用います。つまり、3.3節で述べたように”客の到着時間間隔 t の確率密度が、
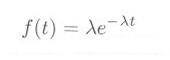 |
・・・・・ |
式4.3.1 |
なる、指数分布にしたがう”ということと、”時間間隔 t 内に k 人の客が到着する確率が、
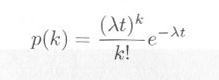 |
・・・・・ |
式4.3.2 |
である”ということが、同等であることを利用します。
| 図4.3.1 ポアソン乱数の作り方 |
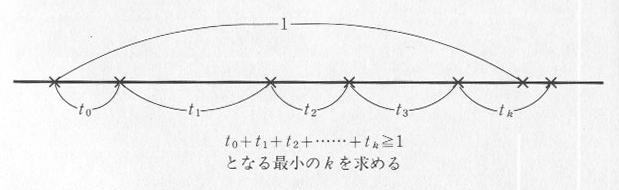 |
図4.3.1に示すように、指数分布乱数、 t1, t2, t3,・・・ を次々に発生させ、その総和が1を越えるまでの k をカウントすれば、その k が求めるポアソン分布乱数となります。すなわち、
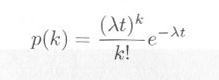 |
・・・・・ |
式4.3.2 |
となる最小の k を求めます。
指数乱数 tn は4.2節で述べたとおり、一様乱数列 rn から
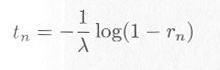 |
・・・・・ |
式4.3.4 |
として求めることができます。いちいち log を計算をしていると時間がかかりますから、
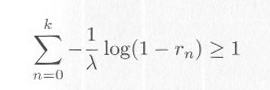 |
・・・・・ |
式4.3.5 |
において、指数関数と対数関数の関係から
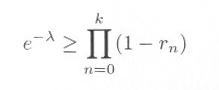 |
・・・・・ |
式4.3.6 |
のとおり変形し、これを満たす最小の k を求めることとします。
プログラムs0430.cの関数
int poisson(double lambda);
は平均 lambda のポアソン乱数を発生します。それをNUMBER回呼んでヒストグラムをつくります。
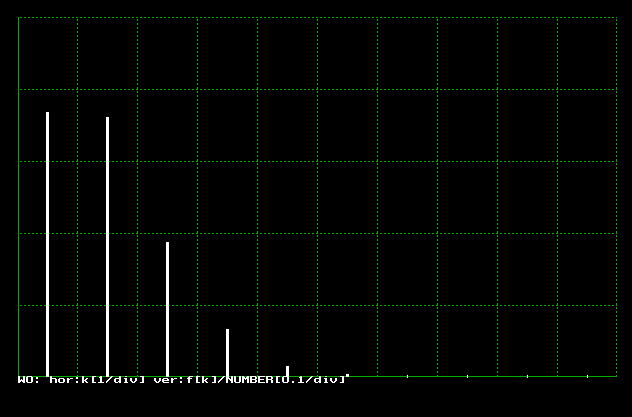
s0430.cの実行結果を図4.3.2に示します。
| 図4.3.2 ポアソン乱数の発生結果 |
 |
| s0430.c ポアソン乱数の発生 |
/* s0430.c
* ポアソン乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include <math.h> /* exp() */
#include "compati.h"
#include "window.h"
#define NUMBER 10000
#define SIZE 20 /* ヒストグラムの大きさ */
int poisson(double lambda);
int main(void)
{
int j; /* forのカウンタ */
int k; /* 本文kの説明参照 */
int f[SIZE] = {0}; /* kの頻度 */
double lambda = 1; /* λ */
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,10,0.5, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "k", 1, "f[k]/NUMBER", 0.1);
setlinestyle(0, 0, 3);
srand(15);
/*メイン*/
for (j = 0; j < NUMBER; j++) {
k = poisson(lambda);
f[k] = f[k] + 1;
}
/*ヒストグラムの表示*/
for (k = 0; k < SIZE; k ++) {
Line(0, k + 0.5, 0, k + 0.5, (double)f[k] / NUMBER);
}
getch();
closegraph();
return 0;
}
int poisson(double lambda)
{
double xp;
int k = 0;
xp = RAND();
while (xp >= exp(-lambda)) {
xp = xp * RAND();
k = k + 1;
}
return (k);
}
|
ア−ラン分布とは
現実のデータを見ると、到着間隔やサービス時間が完全にランダムではなく、前の到着に影響を受け、指数分布にしたがわないことがあります。そのような場合、アーラン分布が用いられます。
r1, r2, r3,・・・rk が互いに独立で、ともに平均が k・λ の指数分布にしたがうとします。そのとき、
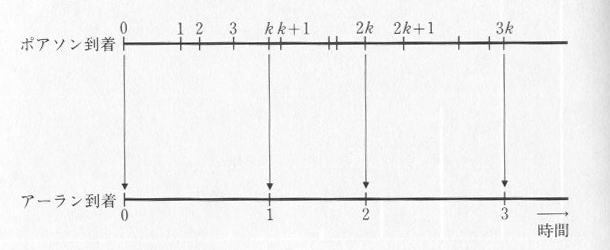
の分布を位相 k のア−ラン分布と言います(注)。ア−ラン分布は、図4.4.1のとおり、ポアソン到着で k 番目ごとの到着のみを着目したとき、その分布に相当します。 k=1 の場合指数分布に一致します。
| 図4.4.1 ポアソン到着と位相 k のアーラン到着 |
 |
指数乱数からア−ラン乱数を作る
さて、位相 k のア−ラン分布の乱数 τ を発生させるには、平均 1/(kλ) の指数分布を
k 個発生させ、その和を τ とすればよろしい。したがって、
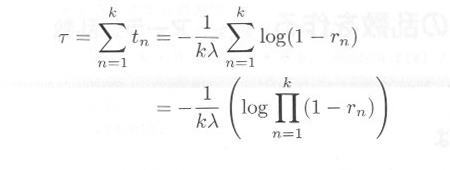 |
・・・・・ |
式4.4.1 |
のようにすれば,時間のかかるlogの計算は1度ですませられます。このプログラムをs0440.cに示します。
double erlang (double lambda, int k);
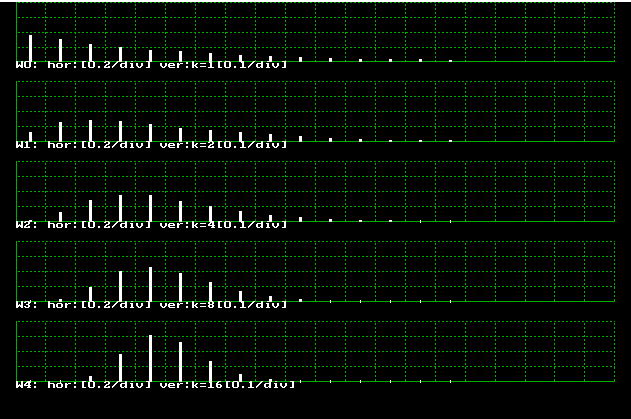
がア−ラン分布の乱数を発生する関数で、よばれるごとに位相 k のア−ラン乱数を返えします。これを NUMBER 回コールし、ヒストグラムを作っています。 K=1, 2, 4, 8, 16 の場合の結果を図4.4.2に示します。
k が大きくなると、中心極限定理にしたがい正規分布に近づいています。指数分布のような極端な非対象の分布でも、たくさん集まれば、正規分布になることは興味深いことです。
| 図4.4.2 アーラン乱数の発生結果 |
 |
| s0440.c アーラン乱数の発生 |
/* s0440.c
* アーラン乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include <math.h> /* log() */
#include "compati.h"
#include "window.h"
#define NUMBER 10000 /* 発生させる乱数の数 */
#define SIZE 15 /* ヒストグラムの大きさ */
#define KIZAMI 0.2 /* 0.2ずつに区切ってヒトグラムへ */
double erlang(double lambda, int k);
int main(void)
{
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int i; /* forのカウンタ */
int f[SIZE] = {0}; /* 頻度 */
int k = 1; /* 位相 k=1,2,4,8,16 */
double lambda = 1; /* λ */
/*グラフィックの準備*/
opengraph();
SetWindow(0, 0.0,0.0,4.001,0.4,SPACE,HIGHT/5-SPACE,WIDTH-SPACE,0);
Axis(0, "", 0.2, "k=1", 0.1);
SetWindow(1, 0.0,0.0,4.001,0.4,SPACE,2*HIGHT/5-SPACE,WIDTH-SPACE,HIGHT/5);
Axis(1, "", 0.2, "k=2", 0.1);
SetWindow(2, 0.0,0.0,4.001,0.4,SPACE,3*HIGHT/5-SPACE,WIDTH-SPACE,2*HIGHT/5);
Axis(2, "", 0.2, "k=4", 0.1);
SetWindow(3, 0.0,0.0,4.001,0.4,SPACE,4*HIGHT/5-SPACE,WIDTH-SPACE,3*HIGHT/5);
Axis(3, "", 0.2, "k=8", 0.1);
SetWindow(4, 0.0,0.0,4.001,0.4,SPACE,HIGHT-SPACE,WIDTH-SPACE,4*HIGHT/5);
Axis(4, "", 0.2, "k=16", 0.1);
setlinestyle(0, 0, 3);
srand(15);
/* メイン */
for (i = 0; i < 5; i ++) {
for (j = 0; j < NUMBER; j++) {
u = (int)(erlang(lambda, k) / KIZAMI);
if (u < SIZE) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
for (u = 0; u < SIZE; u ++) {
Line(i, (u+0.5) * KIZAMI, 0, (u+0.5) * KIZAMI, (double)f[u] / NUMBER);
f[u] = 0;
}
k = k * 2;
}
getch();
closegraph();
return 0;
}
double erlang(double lambda, int k)
{
double tp = 1.0;
double tau;
int n;
for (n = 1; n <= k; n ++) {
tp = tp * (1 - RAND());
}
tau = -1.0 / lambda / (double)k * log(tp);
return (tau);
}
|
正規分布とは
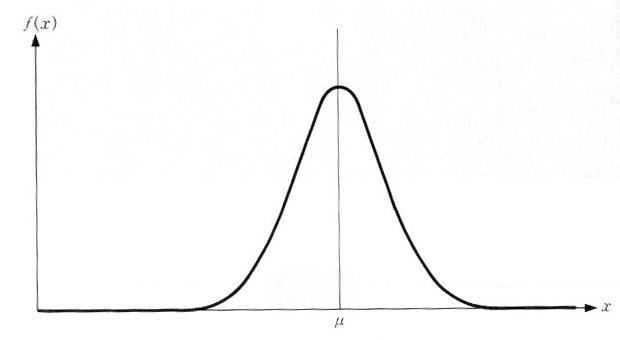
正規分布は、図4.5.1のようによく知られた応用範囲の広い分布で、統計学上も重要です。社会現象の多くのデータ、例えば、身長、学業成績、測定誤差などは、正規分布にしたがいます。
平均 μ 、標準偏差 σ の正規分布の確率密度関数は、
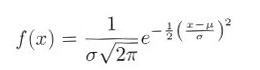 |
・・・・・ |
式4.5.1 |
で与えられ、 μ=0、σ=1 の値を持つ場合を標準正規分布と呼び、
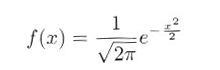 |
・・・・・ |
式4.5.2 |
で示されます。
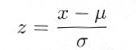 |
・・・・・ |
式4.5.3 |
とおけば、一般の正規分布は、標準化された分布に変換できます。
| 図4.5.1 正規分布 |
 |
中心極限定理による正規乱数
任意の平均と標準偏差を持つ正規分布乱数(正規乱数)を作るには次のとおり、3.5節で述べた中心極限定理を用います。中心極限定理によれば、一様乱数 ri を n 個合計したものの分布は、平均値が n/2 ,分散が n/12 の正規分布に近くなります。したがって、式4.5.3から
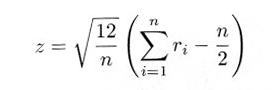 |
・・・・・ |
式4.5.4 |
とおけば、 z の分布は標準正規分布となります。
さらに、任意の平均値 EX 、標準偏差 SD を持つ正規分布は、
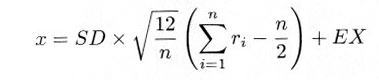 |
・・・・・ |
式4.5.5 |
のように変換することにより得られます。
プログラムs0350.cの結果をもう一度見て下さい。8個の一様乱数を加えあわせると、その分布は十分に正規分布に近いことがたしかめられるので、式4.5.5でそれより大きい n=12 とすれば、平方根の計算をしないですみます。すなわち、
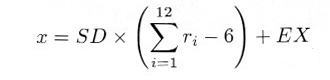 |
・・・・・ |
式4.5.6 |
として,正規乱数を作ることができます。
プログラムs0450.cの関数
double normal(double ex, double sd);
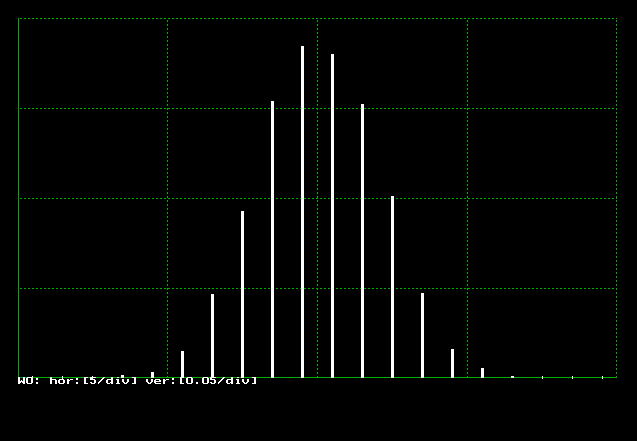
は,平均 ex 、標準偏差 sd の正規乱数を発生します。これを NUMBER 回よんで、ヒストグラムを作ります。この結果を図4.5.2に示します。
| 図4.5.2 正規乱数の発生結果 |
 |
| s0450.c 正規乱数の発生 |
/* s0450.c
* 正規乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include "compati.h"
#include "window.h"
#define NUMBER 10000 /* 発生させる乱数の数 */
#define SIZE 20 /* ヒストグラムの大きさ */
double normal(double ex, double sd);
int main(void)
{
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int f[SIZE] = {0}; /* ヒストグラム */
double ex = 10; /* 平均値 */
double sd = 2; /* 標準偏差 */
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,20.0,0.2, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "", 5, "", 0.05);
setlinestyle(0, 0, 3);
/* メイン */
srand(15);
for (j = 0; j < NUMBER; j++) {
u = (int)(normal(ex, sd));
if (u >= 0 || u < SIZE) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
for (u = 0; u < SIZE; u ++) {
Line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER);
}
getch();
closegraph();
return 0;
}
double normal(double ex, double sd)
{
double xw = 0.0;
double x;
int n;
for (n = 1; n <= 12; n ++) { /* 12個の一様乱数の合計 */
xw = xw + RAND();
}
x = sd * (xw - 6.0) + ex;
return (x);
}
|
度数分布から乱数を作る
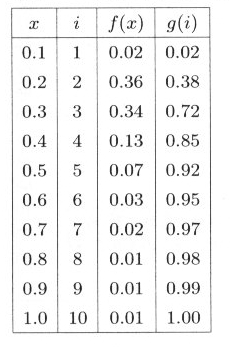
理論分布はわからなくとも、ある現象の統計をとったときの度数分布がわかっている場合、その分布にしたがった乱数を発生させ、再現実実験をすることがで
きます。表4.6.1のような度数分布 f(x) があたえられた時、図4.6.1bのように直線でむすんだ累積分布関数 g(i) に、逆関数法により
一様乱数を代入することにより分布乱数を発生させることにしましょう。
| 表4.6.1 与えられた度数分布 |
 |
| 図4.6.1 累積分布の逆関数による乱数発生 |
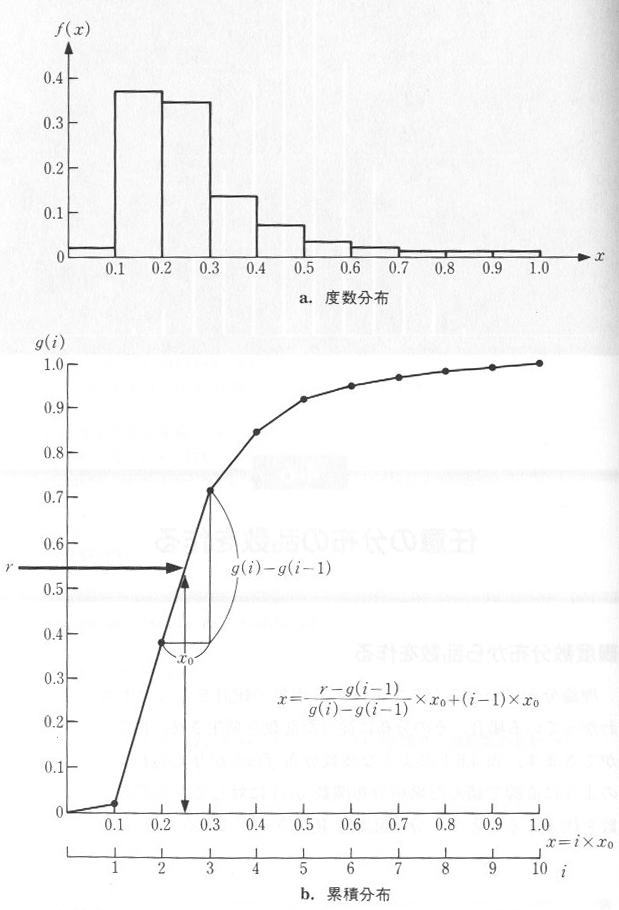 |
まず、 x のキザミ幅を x0 とし、キザミの番号を i としたとき( i=1 から k )、累積分布を表4.6.1のように g(i) とします。プログラムs0460.cの行43のように、表4.6.1の値を配列 g[i] に代入します。
double general(void);
が任意分布乱数発生の関数で、 RAND()マクロにより乱数 r を発生させ、 g[i] の配列を i の小さい方から見ていき、 g[i]>r となったら、その r と i により、
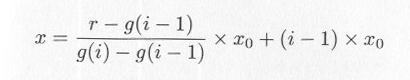 |
・・・・・ |
式4.6.1 |
として x を求めます。プログラムs0460.cの関数
double general(void);
によりこの計算を行ないます。
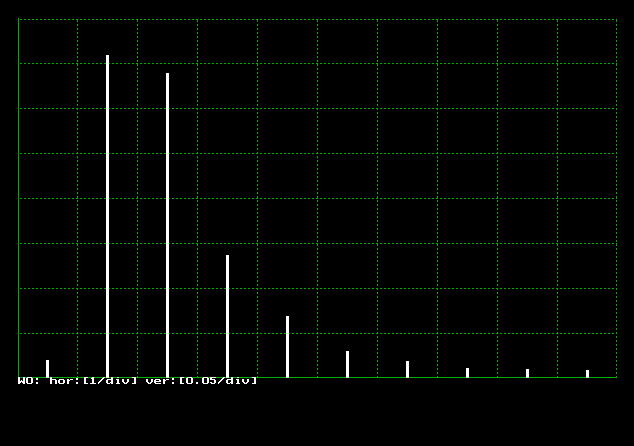
これを実行し、図4.6.1と比べてみてください。図4.6.2のように、もとの度数分布に近い乱数が得られていることが判ります。 g(i) の値に実際の測定データを用いれば、その現象の再現ができます。
| 図4.6.2 任意分布乱数の発生結果 |
 |
| s0460.c 任意分布乱数の発生 |
/* s0460.c
* 任意分布乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include "compati.h"
#include "window.h"
#define NUMBER 10000 /* 発生させる乱数の数 */
#define SIZE 10 /* ヒストグラムの大きさ */
double general(void);
int main(void)
{
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int f[SIZE] = {0};
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,10.0,0.4, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "", 1, "", 0.05);
setlinestyle(0, 0, 3);
/* メイン */
srand(15);
for (j = 0; j <= NUMBER; j++) {
u = (int)(general() * SIZE);
if (u >= 0) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
for (u = 0; u < SIZE; u ++) {
Line(0, u+0.5, 0, u+0.5, (double)f[u] / NUMBER);
}
getch();
closegraph();
return 0;
}
double general(void)
{
double g[SIZE + 1] =
{0.0,0.02,0.38,0.72,0.85,0.92,0.95,0.97,0.98,0.99,1.0};
double x0 = 1.0 / SIZE;
double r,x;
int i = 0;
r = RAND();
while (g[i] < r) {
i = i + 1;
}
x = (r - g[i - 1]) / (g[i] - g[i - 1]) * x0 + (i - 1) * x0;
return (x);
}
|
1. プログラムs0310.cは、ベルヌーイ試行をシミュレートしていますが、 bernoulli() は、二項分布の乱数発生プログラムとしても使えることに注意しなさい。
(解答省略)
2. プログラムs0330.cでも、指数乱数を発生できますが、プログラムs0420.cのほうが高速であることをたしかめなさい。
(解答省略)
3. 区間 [0, 1) の2つの乱数 r1, r2 を発生させ、
とすれば、 x1, x2 は互いに独立な標準正規乱数となります。これを用い、平均 EX 、標準偏差 SD の正規乱数を発生するプログラムを作りなさい。
(解答)
| a0430.c 4章3.の解答 正規乱数の発生 |
/* a0430.c 4章3.の解答
* 正規乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include <math.h>
#include "compati.h"
#include "window.h"
#define NUMBER 10000 /* 発生させる乱数の数 */
#define SIZE 20 /* ヒストグラムの大きさ */
#define PI 3.141593
double normal1(double ex, double sd);
int main(void)
{
int j; /* forのカウンタ */
int u; /* キザミの番号 */
int f[SIZE] = {0}; /* ヒストグラム */
double ex = 10; /* 平均値 */
double sd = 2; /* 標準偏差 */
/* グラフィックの準備 */
opengraph();
SetWindow(0, 0.0,0.0,20.0,0.2, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "", 5, "", 0.05);
setlinestyle(0, 0, 3);
/* メイン */
srand(15);
for (j = 0; j < NUMBER; j++) {
u = (int)(normal1(ex, sd));
if (u >= 0 || u < SIZE) {f[u] = f[u] + 1;}
}
/* ヒストグラムを書く */
for (u = 0; u < SIZE; u ++) {
Line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER);
}
getch();
closegraph();
return 0;
}
double normal1(double ex, double sd)
{
double xw ;
double x;
xw = sqrt(-2.0 * log(RAND())) * cos(2.0 * PI * RAND());
x = sd * xw + ex;
return (x);
}
|
4. 3.5節で述べたとおり、2つの一様乱数の和の分布が、平均1の三角分布となることを用いて、任意の三角分布乱数を発生するプログラムをつくりなさい。
(解答)
| a0440.c 4章4.解答 区間a,bの三角分布乱数の発生 |
/* a0440.c 4章4.解答
* 区間a,bの三角分布乱数の発生
* (C) H.Ishikawa 1994 2018
*/
#include "compati.h"
#include "window.h"
#define NUMBER 10000
#define SIZE 20 /* ヒストグラムの大きさ */
int main(void)
{
int j; /* forのカウンタ */
int u; /* xの整数部分 */
double x; /* 三角分布の乱数 */
double a = 5; /* 三角分布の下限 */
double b = 15; /* 三角分布の上限 */
int f[SIZE] = {0}; /* 頻度 */
/*グラフィックの準備*/
opengraph();
SetWindow(0, 0.0,0.0,20,0.20, SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "x",1, "f[x]/NUMBER", 0.050);
setlinestyle(0, 0, 3);
/*メイン*/
for (j = 0; j < NUMBER; j ++) {
x = (b + a) / 2.0 + ((RAND() + RAND()) - 1.0) * (b - a) / 2.0;
u = (int)x;
f[u] = f[u] + 1;
}
/*ヒストグラムの表示*/
for (u = 0; u < SIZE; u ++) {
Line(0, u + 0.5, 0, u + 0.5, (double)f[u] / NUMBER);
}
getch();
closegraph();
return 0;
}
|
5. 二項分布3.1.2は n が大きく、 k が大きい場合
となり、平均値が np 、分散が npq の正規分布として近似できます。 n = 6 , p = 0.5 の場合のベルヌーイ試行シミュレーション・プログラムs0310.cの結果と、正規乱数発生のプログラムs0450.cで、平均値 = 6×0.5 , 分散 = 6×0.5×0.5 とした場合を比較しなさい。
(解答省略)
|
 |
