 |
|
�Q�D�@�����̓V���~���[�V�����̊�{�|�| �����̔������@�|�|
|
�@���̋K�������Ȃ��ɁA�������N���邱�Ƃ��R���s���[�^�Ŏ�������ɂ́A�ł���߂Ȑ��̗�|�|�����|�|���K�v�ł��B���̏͂ł́A�V�~�����[�V�����ɕK���K�v�ƂȂ�A�����̔������@�ƁA���̐����𗝉����܂��B
�����Ƃ�
�@�����Ƃ́A�Ȃ�炩�̕��@�ŁA�ǂ̐����������m���ŁA�ł���߂ɂȂ�悤�ɑI��ŁA�����̗����������̂ł��B�Ⴆ�A����������ӂ��ďo���ڂ��L�^����A����͂P����U�܂ł̗����ɂȂ�܂��B���邢�́A�P�~�̃A���~�̍d�݂�
�P�O�O���p�ӂ��Ă����A���̂P���A�P���ɁA�O�O�A�O�P�A�O�Q�A�E�E�E�A�X�X�Ƃ����ԍ��������Ă����A������\�������܂��āA�ڂ��Ԃ��Ď��o���A�O�O����X�X�܂ł̗����ƂȂ�܂��B
�R���s���[�^�ɂ�闐�����
�@�R���s���[�^�ŗ�����������ɂ́A�������̕��@������܂����A�Ⴆ���鐔���i������g���ˁh�ƌ����܂��j���Ȃ�ǂ��|�����킹��ƁA�O����X��
�ł̐������قړ����������A�K���������Ȃ��̂ŁA�����������Ďg���܂��B���̂悤�ȕ��@�ō���闐���́A�^�̈Ӗ��̗����ł͂Ȃ��A�^�������ƌ���
�܂��B
�@�R���s���[�^�̋^�������𗐐��Ƃ��Ďg�p����ꍇ�́A���̂悤�ȏ��������Ȃ���Ȃ�܂���B
�@�@��������������
�^�������ł́A�܂������������J��Ԃ��o������ꍇ������܂��B���̎������Z���Ɨ����Ƃ��Ă̈Ӗ����Ȃ��Ȃ�܂��B
�A ���v�I����ɑς��邱��
���Ƃ��A�����������Ƃ��A
�@�@�@�@�@�@�@�@�O�A�@�O�A�@�O�A�@�P�A�@�P�A�@�P�A�@�Q�A�@�Q�A�@�Q�A�@�Q
�Ƃ������A�����̖@���ɏ]���ďo�����鐔��́A�����Ƃ͌����܂���B���Ƃŏq�ׂ铝�v�I����Ƃ������@�ŁA���������܂��B
�B �Č��������邱��
�@�V�~�����[�V�����ɗp����ꍇ�A����̗������g�p���āA�قȂ������f���ŃV�~�����[�V�������A��r��������ꍇ������܂��B�܂��v���O�����̃f�o�b�O���ɂ����x�������n��̗�����K�v�Ƃ���ꍇ������܂��B���Ȃ킿�����ɁA�Č������K�v����܂��B
�C ���������̃X�s�[�h����������
�@�V�~�����[�V�����ł́A���������x���J��Ԃ��p���Ď������s���A������̎������ʂ��畁�Ր��̂��鋤�ʈ��q�����߂܂��B���̂��ߗ��������ɗv����v�Z�X�s�[�h�������Ȃ���Ȃ�܂���B
�@���ɏq�ׂ�悤�ɁC�b����ɂ́Crand()���Ƃ������������@�\������C����́C��L�@�`�C�̏������悭��������܂��B
rand()��
�@rand()���́C�b�̃}�j���A���ɂ��C�W�����C�u�������̃��[�e�B���e�B�istdlib.h�j�̒��ɂ���C
int�@rand(void);
�ƒ�`����Ă���C���̊����Ăяo����邽�тɁC���̐����^�̗�������������܂��B�����^�͈̔͂́C�R���s���[�^���邢�̓R���p�C���ɂ���ĈقȂ�C�ʏ�P�U�r�b�g�̃p�\�R���ł͍ő�32,767�i���Ȃ킿215 - 1�j�C�R�Q�r�b�g�̃��[�N�X�e�[�V�����ł͍ő�2,147,483,647�i���Ȃ킿232 - 1�j�ƂȂ�܂��B rand()������o�͂���闐���́C�O���炱�̐����̍ő�l�͈̔͂ł��B�܂��C�V�X�e���ɂ���ẮCstdlib.h�̒��ŁC�ő�l��
#define RANDMAX 32767
�Ƃ��āC��`����Ă���CRANDMAX�ōő�l��m�邱�Ƃ��ł��܂��B�i�s���������@�b�ł͌���Ă��܂��B�j
�@�{���ɂ����ẮC����rand()�������ׂẴv���O�����ŗp���܂��̂ŁC�ڂ������ׂĂ݂邱�Ƃɂ��܂��傤�B
�@���߂��ɊȒP�ȃv���O���� s0220.c���R���p�C�����Ď��s���Ă݂܂��B���ʂ́C�}�Q�D�Q�D�P�̂Ƃ���ł��B�Q�O�̂O���琮���^�̍ő�l�͈̗̔͂������o�͂���܂����B
�@������x�C���̃v���O���������s���Ă݂Ă��C�o�͓͂����ł��B�b��rand()���ŏo�͂���闐���́C�Č�����������܂��B
| �@ s0220.c �@�@�@rand()���g���Ă݂� |
/* s0220.c rand()�� */
#include <stdio.h> /* printf() */
#include <stdlib.h> /* rand() */
#define NUMBER 20
int main(void)
{
int j,r;
for (j = 1; j <= NUMBER; j++){
r = rand();
printf("%10d\n",r);
}
return 0;
}
|
| �}�Q�D�Q�D�P�@s0220.c�̎��s���� |
 |
�O�ȏ�P�����̗��������|�|RAND()�}�N���|�|
�@�V�~�����[�V�����ŗp���闐���́C�@��ɂ�炸�C�O�ȏ�łP�����ł���ƕ֗��ł��B���̂��߁CsO221.c �̂悤�ɁCrand()���̒l���i�ő�l�{�P�j�Ŋ����Ďg�����ƂƂ��܂��B�ő�l�́C�P�U�r�b�g�n�̃p�\�R���̏ꍇ32767�C�R�Q�r�b�g�n�̃��[�N�X�e�[�V�����̏ꍇ2147483647�ł��Bs0221.c�ł͂��̂��Ƃ��C#define�łP�U�r�b�g�n�̏ꍇ
#define RAND() ((double)rand()/(32767.0+1.0))
�R�Q�r�b�g�n�̏ꍇ
#define RAND() ((double)rand()/(2147483647.0+1.0)
�̂悤�ɁC�}�N���Ƃ��Ē�`���Ă��܂��B�is0221.c�ł́C�����̂����g��Ȃ������폜���邩�C�R�����g�Ƃ��Ė����ɂ��Ă���R���p�C�����ĉ������B�j���̂悤�ɂ��Ă����C�V�~�����[�V�����̃v���O�����ɂ����āC�v���v���b�Z�b�T���C���ׂĂ�RAND()�Ƃ����ӏ��ŁC���̒�`�ɏ]���Ēu�������Ă���܂��B�{���ɂ����ẮC�啶����RAND()���O�ȏ�P�����̗��������@�\�Ƃ������ƂɂȂ�܂��B�Ȃ��C�}�N����`�ł͂Ȃ��C�O�ȏ�P�����̗����������C���Ƃ��Ē�`������@������܂��B
| �@ s0221.c �@�@�@�O�ȏ�P�����̗��� |
/* s0221.c �O�ȏ�P�����̗��� */
#include <stdio.h> /* printf() */
#include <stdlib.h> /* rand() */
/* �P�U�r�b�g */
#define RAND() ((double)rand()/(32767+1.0))
/* �R�Q�r�b�g */
/* #define RAND() ((double)rand()/(2147483647.0+1.0)) */
#define NUMBER 20
int main(void)
{
int j;
double random;
for (j = 1; j <= NUMBER; j++){
random = RAND();
printf(" %1.10f\n", random);
}
return 0;
}
|
| �}�Q�D�Q�D�Q�@s0221.c�̎��s���� |

|
srand()��
�@����rand()���́g���� �h�iseed�j��ݒ肷��srand()�����g���Ă݂܂��Bsrand()���́C
void srand(unsigned seed);
�ƒ�`����C����ɂ��Crand()�����C�j�V�����C�Y���C�������ς��邱�Ƃ��ł��܂��B�v���O����s0222.c�̍s16�̂悤�ɁCsrand(2)�������Ă݂܂��B�������ɁC��قǂƂ͈قȂ��������o�͂���܂��B
| �@ s0222.c �@�@�@rand()���g���Ă݂� |
/* s0222.c �O�ȏ�P�����̗����i���˂�ݒ�j */
#include <stdio.h> /* printf() */
#include <stdlib.h> /* rand() */
/* �P�U�r�b�g */
#define RAND() ((double)rand()/(32767.0+1.0))
/* �R�Q�r�b�g */
/* #define RAND() ((double)rand()/(2147483647.0+1.0)) */
#define NUMBER 20
int main(void)
{
int j;
double random;
srand(2); /*���˂�ݒ�*/
for (j = 1; j <= NUMBER; j ++){
random = RAND();
printf(" %1.10f\n", random);
}
return 0;
}
|
| �}�Q�D�Q�D�R�@�@s0222.c�̎��s���� |

|
���s���邲�ƂɈقȂ����n��̗�����������
�@rand()���́C���˂������ł��邩����C����n��̗��������܂��B����́C�V�~�����[�V�����v���O�����̃f�o�b�O���ɂ́C���s���邲�Ƃɓ���̌��ʂ������C��ϓs������낵���B�������C�ꍇ�ɂ���ẮC���s���邲�Ƃɕʌn��̗��������������ꍇ������܂��B����ɂ́C���̂悤��
srand()���̂��˂�time()���Ŏ��s���邲�Ƃɕς��邱�Ƃɂ������ł��܂��B
srand((unsigned)time(NULL));
��l�ɕ��z���Ă��邩
�@�b�̗������C�{���Ɉ�l���z���Ă��邩�ǂ����ׂ܂��B�v���O����s0230.c�̂悤�ɁCRAND()�}�N���ŗ��������X���������C0.1���Ƃ̃L�U�~���C0�`0.1, 0.1�`0.2, 0.2�`0.3, ����ɂ��ꂼ�ꉽ���邩���J�E���g���Ă݂܂��s0230.c�̍s24�ŗ����������C���ꂼ��̃L�U�~�ɑΉ����Ci= 0, 1, 2, 3, ���,9 �ƂȂ�悤�ɂP�O�{���C�������������o���Ă��܂��B�s25�ł́C���ꂼ��̃L�U�~�ɁC���������邩��f[i]�Ƃ��ăJ�E���g���܂��B
���_���z�Ƃ̔�r
�@�Ƃ���ŁC���_���zf0��10000 / 10 = 1000�ƂȂ�͂��ł����C�v���O����s0230.c�̌��ʂ��C�ʂ����āC��l�����ƌ�����̂��S�z�ɂȂ�܂��B��ʂɓ��v�w�ł͕�W�c���T���v�����O���ē���ꂽ���z�ƁC���m�̕��z�Ƃ̊Ԃɍ������邩�ǂ����肷�邱�Ƃ��C�g�K���x�̌���h�i�ȉ��ł͒P�Ɍ���j�ƌ����܂��B�Ⴆ�C�S�����̔N�ߕʂ̍\�����킩���Ă��鎞�C�����s���̔N�ߍ\�����S���ƍ������邩�ǂ������C�����s���̐��S�l�̔N�ߍ\�������C���̃T���v�����O�E�f�[�^���画�f����ꍇ�ȂǂɁC���̌��肪�p�����܂��B
�@�����قǂ́C��l���������̗�ł́C�T���v�����O�E�f�[�^��f(i)�C���m�̕��z��f0 = 1000�ɑ������܂��B
����
�@����́C���̂悤�ɍs�Ȃ��܂��B
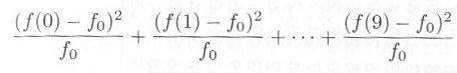 |
�E�E�E�E�E |
���Q�D�R�D�P |
�Ƃ������̂��l���Ă݂܂��B�����ʏ�@��2�@�i�J�C����Ɠǂށj�ƌ����܂��B���̗ʂ́A�T���v�����O�E�f�[�^�ƁA���_�x���Ƃ̂����Ⴂ�̒��x��\�킵�Ă��܂��B�����T���v�����O�E�f�[�^�Ɨ��_�x���̂����Ⴂ���܂������Ȃ���A��2 = 0 �ƂȂ�A�����Ⴂ���傫���قǁ@��2�@ �͑傫���Ȃ�܂��B
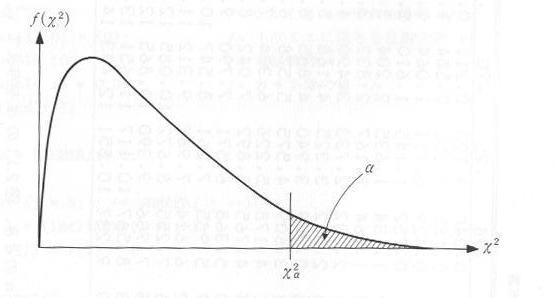
�@������W�c����̃T���v�����O�̂����́A���ʂ������̂ŁA�@��2�@�́h��2���z�h�Ƃ������z�ɏ]�����Ƃ��m���Ă��܂��B��2���z�͎��R�x�ƌĂ��p�����[�^�������Ă��āA���̗�ł͂X�i�L�U�~�̐��|�P�j�ł��B��2���z�͐}�Q�D�R�D�P�̂悤�Ȍ`�����Ă���A��2���z�\���\�Q�D�R�D�P�Ɏ����܂��B���̕\�́A �@����2 �@�Ɓ@ ����2 �@�̉E���̖ʐσ��̊W��\�킵�Ă���A�T���v�����O�E�f�[�^���瓾��ꂽ �@��2 �@���@����2�@��菬������A�h�댯�����ŗ��_�x���ƃT���v�����O�E�f�[�^���������h�ƌ����邱�ƂɂȂ�܂��B
| �}�Q�D�R�D�P�@��2���z |
 |
�p�x����̃v���O����
�@�v���O����s0230.c�́@�s32�� xs �Ƃ��� ��2�@���v�Z���Ă��܂��B���̃v���O�����̏o�͂͐}�̂悤�ɁC��2 = 9.17�ƂȂ�܂��B����A�\�Q�D�R�D�P����댯���T���� ����2 �� 16.919 �ł�����Axs �͂��̒l��菬�����A���������ĂT���̊댯���ň�l���z�ł���ƌ����Ă悢���Ƃ��킩��܂��B���Ȃ킿�ARAND()�̕p�x�e�X�g�͍��i�������ƂɂȂ�܂��B
| �@ s0230.c �@�@�p�x����v���O���� |
/* s0230.c �p�x���� (C) H.Ishikawa 1994 2018*/
#include <stdio.h> /* printf() */
#include <stdlib.h> /* rand() */
/* �P�U�r�b�g */
#define RAND() ((double)rand()/(32767.0+1.0))
/* �R�Q�r�b�g */
/* #define RAND() ((double)rand()/(2147483647.0+1.0))*/
#define NUMBER 10000 /* ���������闐���̐� */
int main(void)
{
int j; /* for�̃J�E���^ */
int i; /* 0.1���Ƃ̃L�U�~�̔ԍ� */
int f[10] = {0}; /* �L�U�~i�ɗ����闐���̐� */
double f0; /* ���_�x�� */
double xs = 0.0; /* �J�C����̒l */
srand(15);
f0 = NUMBER/10.0;
for (j = 1; j <= NUMBER; j ++){
i = (int)(RAND() * 10);
f[i] = f[i] + 1;
}
printf(" i f[i]\n");
/*�p�x�̌���*/
for (i = 0; i <= 9; i ++){
printf("%10d %10d\n", i, f[i]);
xs = xs + (f[i] - f0) * (f[i] - f0) / f0;
}
printf("xs = %f\n", xs);
return 0;
}
|
| �}�Q�D�R�D�Q�@s0230.c�̎��s���� |

|
�|�[�J����Ƃ�
�@�p�x����l������ƌ����āA�������Ɉ�l�����ł���Ƃ͌����܂���B�Ⴆ�A
�@�@�@�@0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, ����
�͕p�x����ɂ͍��i���܂����A�J��Ԃ����K���I�ŗ����Ƃ͔F�߂��Ȃ��ł��傤�B�|�[�J����́A���K�����̌���̎�@�ŁA�����̗����̗��A�����ĂT��
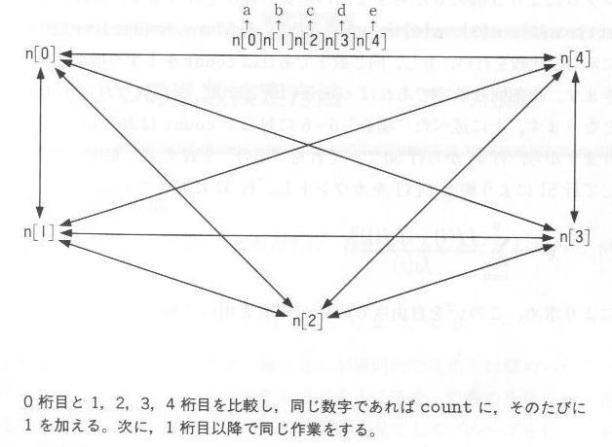
�܂Ƃ߁A�T���̐����Ƃ݂ăO���[�v�����A�g�����v�̃|�[�J�Ɠ����悤�Ɏ������Ē��ׂ܂��B�O����X�̎�ނ̃J�[�h���T���������ƍl����ƁA���́h
�ꍇ�h������܂��B
�O�@ abcde: �@5�̐������S���قȂ��Ă���B
�P�@ aabcd: �@���������Q����Ȃ�y�A����g����B
�Q�@ aabbc: �@�y�A����g����B
�R�@ aaabc: �@�����������R����B
�S �@aaabb: �@�����������R�ƁA�y�A���P����B
�T�@ aaaab: �@�����������S����B
�U�@ aaaaa: �@�S���̐����������ł���B�@
�@�����̋N����m���͗��_�I�ɋ��߂��A���̒l���\�Q�D�S�D�P�Ɏ����܂��B
�|�[�J����̃v���O����
�@���̗��_�l�ƁC���ۂɃR���s���[�^�Ŕ����������^�������ɂ�鐔���̂Ȃ�тƔ�r���Ă݂܂��傤�B�v���O���� s0240.c�ł́C�s33����s35�ɂ����āCRAND()�}�N���ɂ��T�̂O����X�܂ł̐����̂Ȃ�т����܂��B����� n[0], n[1], n[2], n[3], n[4] �Ƃ��܂��B���ɍs37����s43�ɂ����āC�}�Q�D�S�D�P�̂Ƃ���̔�r���s���C�������������ł���Ccount���P���������Ă����܂��B�S�����������ł����count = 10�ƂȂ�C�S���قȂ��count = 0�ƂȂ�܂��B��ɏq�ׂ��h�ꍇ�h�O�`�U�ɑ��āCcount���\�Q�D�S�D�P�̒l���Ƃ�܂�����C�s44����s50�ŁC������h�ꍇ�h��\�킷 i �ɕϊ����܂��B�����čs51�ɂ��C�p�xf[i]���J�E���g���C�s57�ɂ����āC��2��
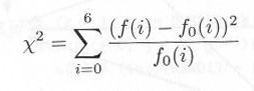 |
�E�E�E�E�E |
���Q�D�S�D�P |
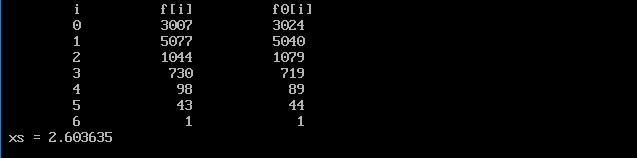
�ɂ����Ƃ߁A���� ��2�@�����R�x�U ����2 ���z�\��p���Č��肵�܂��B
�@���̃v���O�����̎��s���ʂ�}�Q�D�S�D�Q�Ɏ����܂��B��2�̒l�� 2.602�ƂȂ�C�b��RAND()���́C�|�[�J�e�X�g�ɂ����Ă����i���܂��B
| �}�Q�D�S�D�P�@�|�[�J�[�e�X�g�̕��@ |
 |
| �@s0240.c �|�[�J���� |
/* s0240.c �|�[�J���� (C) H.Ishikawa 1994 2018*/
#include <stdio.h> /* printf() */
#include <stdlib.h> /* rand() */
/* �P�U�r�b�g */
#define RAND() ((double)rand()/(32767.0+1.0))
/* �R�Q�r�b�g */
/* #define RAND() ((double)rand()/(2147483647.0+1.0)) */
#define NUMBER 10000 /* ���������闐���̐� */
int main(void)
{
int i; /* �\�Ɏ���i */
int count; /* �\�Ɏ���count */
int j, j1, j2, k; /* for�̃J�E���^ */
int f[7] = {0}; /* i���Ƃ̓x�� */
int f0[7]; /* ���_�x�� */
int n[5]; /* �T�̐����̕��� */
double xs = 0.0; /* �J�C����l */
double diff; /* ���_�l�Ƃ̍� */
srand(2);
f0[0] = NUMBER * 0.3024;
f0[1] = NUMBER * 0.5040;
f0[2] = NUMBER * 0.1080;
f0[3] = NUMBER * 0.0720;
f0[4] = NUMBER * 0.0090;
f0[5] = NUMBER * 0.0045;
f0[6] = NUMBER * 0.0001;
for (k = 1; k <= NUMBER; k ++){
for (j = 0; j < 5; j ++){
n[j] = (int)(RAND() * 10);
}
count = 0;
for (j1 = 0; j1 < 4; j1 ++){
for (j2 = j1 + 1; j2 < 5; j2 ++){
if (n[j1] == n[j2]) {
count = count + 1;
}
}
}
if (count == 10){
i = 6;
} else if (count == 6){
i = 5;
} else{
i = count;
}
f[i] = f[i] + 1;
}
printf(" i f[i] f0[i]\n");
for (i = 0; i <= 6; i++){
printf("%10d %10d %10d\n", i, f[i], f0[i]);
diff = f[i] - f0[i];
xs = xs + diff * diff / f0[i];
}
printf(" xs = %f\n", xs);
return 0;
}
|
| �}�Q�D�S�D�Q�@s0240.c�̎��s���� |
|
�@�P�D�@�v���O�����@s0230.c�ŁC���˂̒l��ς��Ď��s���C ��2�̒l���ǂ��ς�邩�C���ׂȂ����B
�@�@�i�ȗ��j
�@�Q�D�@�P����U�܂ł̐��������m���ŏo�����邳������̃V�~�����[�V�������s�Ȃ��Ȃ����B����������ӂ邽�тɁC�ł���߂Ȑ����ł�悤�ɂ��Ȃ����B
�@�@�i�j�@
| �@a0220.c �@�@�Q�͂Q�D�̉� |
/* a0220.c �Q�͂Q�D�̉�
* �T�C�R��
* (C) H.Ishikawa 1994 2018
*/
#include <time.h>
#include <stdio.h>
#include <stdlib.h>
/* �P�U�r�b�g */
#define RAND() ((double)rand()/(32767.0+1.0))
/* �R�Q�r�b�g */
/* #define RAND() ((double)rand()/(2147483647.0+1.0)) */
#define END 20
int d;
int t;
int main(void)
{
srand((unsigned)time(NULL)); /* �����n���� */
for (t = 1; t <= END; t ++) {
d = (int)(RAND() * 6.0) + 1;
printf("%d\n",d);
}
returen 0;
}
|
�@�R�D�@�P���̋�ԂO����X�܂ł̗������������Ƃ��C��������������܂ł̊Ԋu���C�M���b�v�Ƃ����܂��B���̒�����r�ł���m���́C
�ŕ\�킳��܂��ir = 0�́C�����ē�������������ꂽ�ꍇ�j�B���̂��Ƃ�p���āC�b�̗����̃M���b�v������s�Ȃ��Ȃ����B
�@�@�i�j
| �@a0230.c �@�@�Q�͂R�D�̉� |
/* a0230.c �Q�͂R�D�̉�
* �M���b�v����
* (C) H.Ishikawa 1994 2018
*/
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
/* �P�U�r�b�g */
#define RAND() ((double)rand()/(32767.0+1.0))
/* �R�Q�r�b�g */
/* #define RAND() ((double)rand()/(2147483647.0+1.0)) */
#define NUMBER 10000
long r = 0; /* �M���b�v */
long n; /* ����������for */
long m; /* ���������o���� */
long f[100] = {0}; /* �M���b�v�̕p�x */
double f0; /* ���_�l */
double xs = 0.0; /* �J�C����l */
int main(void)
{
for (n = 1; n <= NUMBER; n ++) {
/* 0�̏o��Ԋu�ׂ� */
if ((long)(RAND() * 10.0) == 0) {
f[r] = f[r] + 1;
m = m +1;
r = 0;
} else {
r = r + 1;
}
}
for ( r = 0; r <= 19; r ++) {
f0 = pow((1.0 - 0.1),(double)r) * 0.1 * (NUMBER / 10);
printf("%6ld %6ld %6.4f\n", r, f[r], f0);
xs = xs + ((double)f[r] - f0) * ((double)f[r] - f0) / f0;
}
printf("xs = %f\n", xs);
return 0;
}
|
|
 |
