 |
|
�P�O�D�@���ł��V�~�����[�V�������Ă݂悤
|
�@�{���̍Ō�́A�u���ł��V�~�����[�V�������Ă݂悤�v�Ƒ肵�A�M�����u������A�ŋߒ��ڂ���Ă���A�W�F�l�e�B�b�N�A���S���Y���܂ŁA������p�����A���܂��܂ȁA�m���������A���݂܂��B
�N���b�v�X�Ƃ������̃Q�[�������i�W�j�i�P�R�j
�@�J�W�m�ōs���Ă���_�C�X�i�T�C�R���j���g�����A�N���b�v�X�Ƃ����Q�[�����Ƃ肠���܂��B���̃N���b�v�X�Ɍ��炸�A�J�W�m�ōs����Q�[���́A���ׂ�
�������L���ƂȂ�悤�ȃ��[������߂��Ă��܂��B���������Ē����ԕ��ς���A�K�����������d�g�݂ƂȂ��Ă���킯�ł����A�K���@�͂Ȃ����̂ł��傤
���B
�@�܂��A�N���b�v�X�̃��[����������܂��B�N���b�v�X�͂Q�̃T�C�R����p���Ă����Ȃ��܂��B�Q�̃T�C�R���̖ڂ̍��v�͂Q����P�Q�܂ł̒l���Ƃ��
���B�i�R�D�T�߂Ŏ������Ƃ���A�V�̏o��m�����ł��傫���B�j�v���[���͂Q�̃T�C�R����U���āA���̘a���V�܂��́A�P�P�̎��i������i�`�������Ƃ�����
���j�͏�����,�Q�A�R���邢�͂P�Q�̎��i������N���b�v�X�Ƃ����܂��j�͕����ł��B��������ȊO�̂Ƃ��A���Ȃ킿�A�S�A�T�A�U�A�W�A�X�܂��́A�P�O���ł�
�Ƃ��́A���̒l���|�C���g�Ƃ����A�Ђ��Â������|�C���g�܂��͂V���o��܂ŁA�T�C�R����U��܂��B�����ē����|�C���g���ł�A�v���[���̏����A�����
�O�ɂV���o��A�����ƂȂ�܂��B�����v���[�������ĂA�����̓q�����̂Q�{�̕����߂����܂��B
�@���̃Q�[���́A�����ւ�悭�ł��āA�����͂��Ȋm���̍��ŁA���������悤�ɂł��Ă��܂��B
�K���@
�@���̃Q�[���ŕK���v���[���������@�͂���ł��傤���B�������ꂪ����A���ЃJ�W�m�ɍs���Č��������̂ł��B�{���@�Ƃ����K���@���m���Ă��܂��B�{
���@�Ƃ����̂́A�܂��P�h���̓q��������X�^�[�g���A�������ĂA�����P�h����q���܂����A�������ꍇ�͂Q�h�����A����ɕ�����ΑO��̓q�����̂Q�{�̊z
�����X�ɓq���Ă������@�ł��B���̕��@�ł́A���������z���Ƃ���ǂ���̂ŁA�K���@�ƂȂ肻���ł��B�͂����āA���ꂪ�ق�Ƃ��ɕK���@�ƂȂ�̂ł��傤
���B�N���b�v�X�ɂ����āA�{���@���V�~�����[�V�������Ă݂܂��傤�B
�V�~�����[�V�����E�v���O����
�@�ł̓N���b�v�X�̃V�~�����[�V�����v���O����s1010.c�̐������s�Ȃ��܂��B�܂��A�T�C�R���̊������܂��B
�@�@ int dice(void);
�ɂ��A�����P�`�U�̈�l���z�̗����������܂��B���ɁA(2)�̂Ƃ���N���b�v�X�̃��[���ǂ���ɋL�q���āA��
�@�@ int craps(void);
�����܂��B�P��ڂ̃T�C�R���̖ڂ̘a�� sum1 , �Q��ڈȌ�̃T�C�R���̖ڂ̘a�� sum2 �Ƃ��Ă��܂��B���̊��́A�����̏ꍇ�P�A�����̏ꍇ�O�̒l��Ԃ��܂��B
�@���Ƀ��C���v���O�����ł����A�P��̓q������ k �h���A���݂̎������� q �h���Ƃ��܂��B�s30����s35���{���@�ɂ��q���ŁA�����������ꍇ�A���̓q�������P�Ƃ��A�������ꍇ�O��̂Q�{��q���邱�ƂƂ��܂��B�v���O�����ł́A�q����������J��Ԃ��A�����q���̉� t �A�c�������� q ���O���t�ɕ\������悤�ɂ��Ă��܂��B
�V�~�����[�V�����̌���
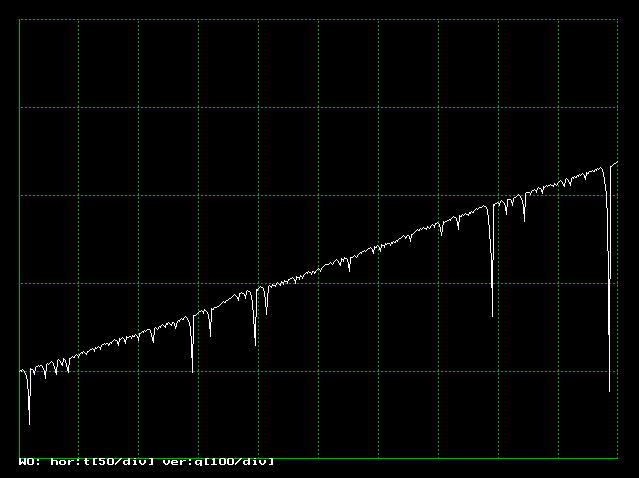
�@�v���O���������s����ƁA�}�P�O�D�P�D�P�̂悤�Ɏ��ԂƂƂ��ɁA�����Ɏ������͑������Ă����܂����A���X�����������Ɠq�������}�����A�Ԏ��ɓ]�������
��������܂��B�������̎��A���������Ȃ��Ȃ�Δj�Y�ł����A�Ȃ��]�T�������Ĕ{�X�Ɠq���邱�Ƃ��ł���A�K���v���X�ɂȂ�܂��B�������Ȃ���A�ʏ�͓�
���̂ق��������͖L�x�ŁA�����������Ă���������������̂ɑ��A�q�̂ق�����ɒ�����Ă��܂��܂��B�����\���Ȏ�����p�ӂ��邱�Ƃ��ł���A����
�J�W�m�֍s���āA�ЂƖׂ����ĉ������B
| �}�P�O�D�P�D�P�@�{���@�ɂ��K���@ |
 |
| �@ s1010.c �M�����u���K���@ |
/* s1010.c
* �M�����u���K���@
* (C) H.Ishikawa 1994 2018
*/
#include <time.h> /* time() */
#include "compati.h"
#include "window.h"
#define T_END 500
long t; /* �N���b�N */
long q = 100; /* ������ */
long k = 1; /* �P��̓q�� */
int dice(void);
int craps(void);
int main(void)
{
opengraph();
SetWindow(0, 0.0,0.0,(double)T_END,500.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "t", T_END/10, "q", 100);
MoveTo(0, 0.0, q);
srand((unsigned)time(NULL)); /* �V�~�����[�V�����̓s�x�����n���ς��� */
for (t = 1; t <= T_END; t ++) {
q = q - k;
if (craps() == 1) { /* �������ꍇ */
q = q + 2 * k;
k = 1; /* �P�h���q���� */
} else { /* �������ꍇ */
k = k * 2; /* �Q�{�q���� */
}
LineTo(0, (double)(t), (double)(q));
}
getch();
closegraph();
return 0;
}
int dice(void)
{
return((int)(RAND() * 6.0 + 1));
}
int craps(void)
{
int r; /* 1:���� 0:���� */
int sum1; /* �a�P */
int sum2; /* �a�Q */
sum1 = dice() + dice();
if (sum1 == 7 || sum1 == 11) { /* �i�`������ */
r = 1;
} else if(sum1 == 2 || sum1 == 3 || sum1 == 12) { /* �N���b�v�X */
r = 0;
} else {
sum2 = 0;
r = 0;
while (sum2 != 7) { /* �V���o��܂� */
sum2 = dice() + dice();
if (sum2 == sum1) { /* �|�C���g */
r = 1;
break;
}
}
}
return(r);
}
|
�ɊǗ����Ƃ�
�@�I�y���[�V�����Y���T�[�`�̋��ȏ��Ɋւ炸�o�Ă�����ł��B��Ƃ�Y�ƃV�X�e���ł́A������i������������v�Ќ������ė���Ă����ߒ��ɂ����āA����������@�\���K�v�ł��B���̒����e�ʂƁA������^�p�Ǘ�����œK�̕��@�����肷��̂��A�ɊǗ����ł��B
�@�Ⴆ�A���鏤�X�����i��≮����d����āA�q�ɔ̔�����ꍇ���l���Ă݂܂��傤�B���i����x�ɑ��ʎd�����ƁA�ɂ������������A���̂��߂̔�p
�������݂܂��B�t�ɏ��ʂ̍ɂł́A�傫�Ȏ��v���������ꍇ�ɕi��̊댯�������A���ׂ��肵���v�������Ȃ��A�Ђ��Ă͂��̓X�̐M�p�������܂��B������
�A�@�@�ɂɗv�����p�A�A�@�≮�ւ̔����̂��߂̔�p�A�B�@�i�ꂪ���������ꍇ�ɂ����ނ鑹���̍��v���ŏ��ɂ��āA���v���ő�ɂ���ɂ́A���ǂ�
�����≮�ɔ������ׂ��ł��傤���B
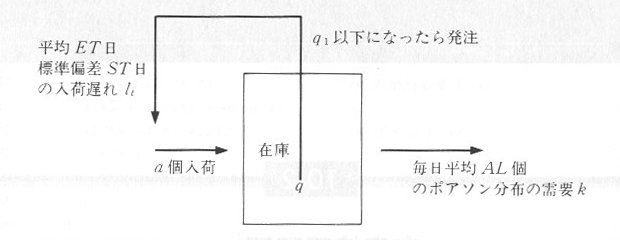
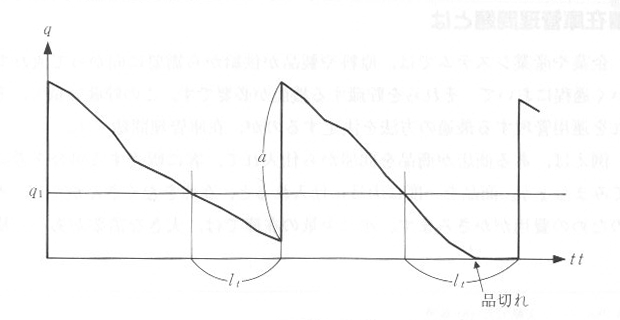
�@�̔��X�̍� q �́A�}�P�O�D�Q�D�P�̂悤�ɖ����̔��グ k ���������Ă����܂��B������_ q1 ���������A a �̔��������܂����A�����ɂ͓��ׂ����A lt ���̒x�ꂪ����܂��B�}�P�O�D�Q�D�Q�̂悤�ɁA�ɗʂ͕ω�����ł��傤�B���グ���Ɠ��ׂ����ꂪ�m���I�ł���ꍇ���l���A ������_q1 �̍œK�l�����߂邽�߂̃V�~�����[�V�����E�v���O����������Ă݂܂��傤�B
| �}�P�O�D�Q�D�P �Ƀ��f�� |
 |
| �}�P�O�D�Q�D�Q�@�� q �̕ω��� lt |
 |
�v���O�����̃|�C���g
�@���グ���́A�������� AL �̃|�A�\�����z�ɏ]���Ƃ��܂��B�܂����גx����� lt �͕��� ET �A�W���� ST �̐��K���z�ɂ����������̂Ƃ��܂��B�����̗����̔����ɂ͂S�͂ō��������p���܂��B�V�~�����[�V�����E�v���O�����̕����͂P�����N���b�N�Ƃ��Đi�߂�Œ莞�ԕ�����p���܂��B�v���O����s1020.c�̍s60����s78���C�P�������^�����܂��B�����ŏd�v�ȕϐ��́A���גx����� lt �Ŏ��̈Ӗ��������܂��B
�@�@�@lt > 0 �F���łɔ������݂ł���A���� lt ���Ŕ[�i�����B
�@�@�@lt = 0 �F�{���[�i�����B
�@�@�@lt < 0 �F�������Ă��Ȃ��B
�@�s61�łP������ k �|�A�\�����z�̔��グ���������Ƃ��܂��B�s64�Ŕ����_ q1 ������A�܂��������Ă��Ȃ���Δ������܂��B�s68�� q �����ɂȂ�A�ɂȂ��Ŕ̔��������Ȃ����� ls �𐔂��܂��B�s73�ł́A�{���[�i���ꂽ�̂ŁA�ɂ� A �������܂��B�s75�ōɔ�p�̗v���v�Z���܂��B T_END �����̃V�~�����[�V�������I��������ƁA������p�̗v sc2 �A�i�ꑹ���̗v sc3 �A������̗v yk ���v�Z���A���v rr �����߂܂��B�����ăO���t���v���b�g���A�����_ q1 �������A�V�~�����[�V�����𑱂��܂��B
�A�E�g�v�b�g
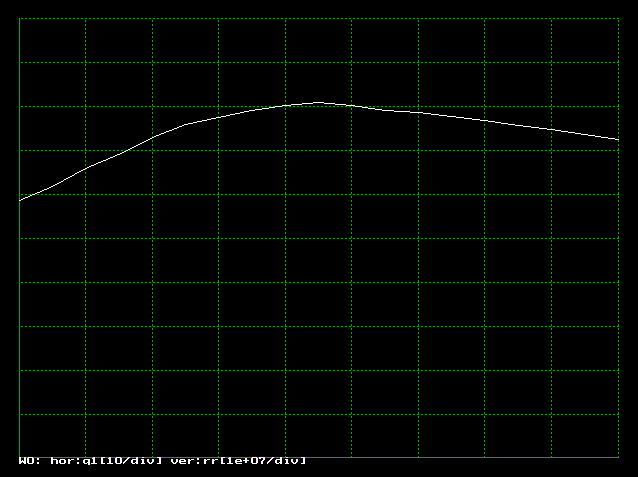
�@�P�O�O�O�O�����̃V�~�����[�V������ q1 ���O����P�O�O�܂ŕω������A�J��Ԃ��s���܂��B �����_ q1�ɑ��鑍���グ rr�̃O���t�}�P�O�D�Q�D�R������ƁAq1=45 �̎��ɁA���v���ő�ƂȂ邱�Ƃ��킩��܂��B
| �}�P�O�D�Q�D�R�@�ɊǗ��̖��@�V�~�����[�V�������� |
 |
| �@ s1020.c �@�@�ɊǗ��̖�� |
/* s1020.c
* �ɊǗ��̖��
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h>
#include <math.h>
#include "compati.h"
#include "window.h"
#define A 100 /* �P��̓��ח� */
#define AL 5 /* �P���̕��ϔ���� */
#define ET 6 /* �[�i����܂ł̕��ϓ��� */
#define ST 2 /* �[�i����܂ł̓����̕W���� */
#define SP 7000.0 /* ���l */
#define PC 5000.0 /* �d����P�� */
#define C1 20.0 /* �P���P������̍ɔ�p */
#define C2 10000.0 /* �P��̔����ɂƂ��Ȃ���p */
#define C3 500.0 /* �i��P������̑��� */
#define T_END 10000
#define Q1_MIN 0
#define Q1_MAX 90
long poisson(double lambda);
double normal(double ex, double sd);
int main(void)
{
long tt; /* �V�~�����[�V�������� */
long q; /* ���ݍɗ� */
long q1; /* �����_ */
long k; /* �P���̔���� */
long zk; /* k�̗v */
long yk; /* ������̗v */
long ls; /* �Ɋ���̂��ߔ��葹�Ȃ����� */
long nn; /* ������ */
long lt; /* ���גx����� */
double sc1; /* �ɔ�p�̗v */
double sc2; /* ������p�̗v */
double sc3; /* �i�ꑹ���̗v */
double rr; /* ���v */
/* �O���t�B�b�N���� */
opengraph();
SetWindow(0, 0.0,0.0,Q1_MAX,1.0e08,
SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "q1", 10, "rr", 1e07);
setlinestyle(0, 0, 2);
//printf(" q1 yk ls nn sc1 sc2 sc3 rr\n");
/* �J�n */
for (q1 = Q1_MIN; q1 <= Q1_MAX; q1 = q1 + 5) {
/* �����ݒ� */
srand(113);
tt = 0; q = A; zk = 0; ls = 0; nn = 0; lt = -1;
sc1 = 0.0; sc2 = 0.0; sc3 = 0.0;
/* �P�����̃V�~�����[�V���� */
while (tt <= T_END) {
k = poisson(AL); /* k���ꂽ */
q = q - k;
zk = zk + k;
if (q < q1 && lt < 0) { /* �����_���������̂Ŕ������� */
lt = (long)normal(ET, ST);
nn = nn + 1;
}
if (q < 0) { /* �Ɋ���̂��ߔ��葹�Ȃ� */
ls = ls - q;
q = 0;
}
if (lt == 0) { /* ���� */
q = q + A;
}
sc1 = q * C1 + sc1;
lt = lt - 1;
tt = tt + 1;
}
sc2 = nn * C2;
sc3 = ls * C3;
yk = zk - ls;
rr = (SP - PC) * yk - sc1 - sc2 - sc3;
//printf("%4ld %6ld %6ld %6ld %8.0f %8.0f %8.0f %8.0f\n", q1, yk, ls, nn, sc1, sc2, sc3, rr);
if (q1 == Q1_MIN) {
MoveTo(0, q1, rr);
} else {
LineTo(0, q1, rr);
}
}
getch();
return 0;
}
long poisson(double lambda)
{
double xp = RAND();
long k = 0;
while (xp >= exp(-lambda)) {
xp = xp * RAND();
k = k + 1;
}
return (k);
}
double normal(double ex, double sd)
{
double xw = 0.0;
double x;
long n;
for (n = 1;n <= 12; n ++) { /* 12�̈�l�����̍��v */
xw = xw + RAND();
}
x = sd * (xw - 6.0) + ex;
return (x);
}
|
�S�͋�������
�@�{�߂ł́A�V�~�����[�V�����Z�p��p���āA�P�P�̌��q�̓������v�Z���A�����S�̂Ƃ��Ăǂ����������������Ă��邩���A�S�̂悤�ȋ������̂��ɉ�͂��Ă݂܂��傤�B
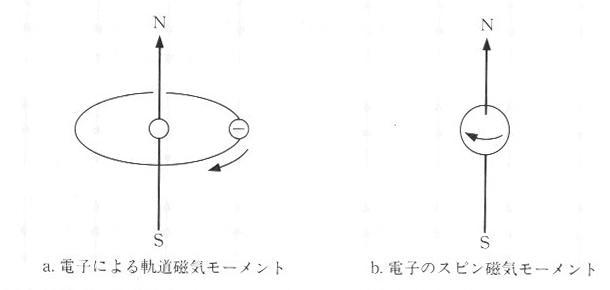
�@���q�̖͌^�́A�}�P�O�D�S�D�P�̂悤�ɁA���q�j�̂܂���d�q���܂���Ă���悤�ɏ����܂��B�d�q�̓}�C�i�X�̓d�C�������Ă���A�d�q����]�^�������
���ꂪ�ł��܂��B���̎��͌��q�̒��S��ʂ�A�d�q�̋O���ʂɑ��Đ����ł��B���̎���̂��Ƃ�d�q�̋O�����C���[�����g�ƌ����܂��B�܂��d�q�͎��]���Ȃ�
�玲�̂܂�������Ă���A����ɂ���Ă��A���ꂪ�����Ă��܂��B������X�s�����C���[�����g�ƌ����܂��B�������ނ̎��C���[�����g���������킳��A
���q�P�̎��C���[�����g�ƂȂ�܂��B
| �}�P�O�D�S�D�P�@���q�̖͌^ |
 |
�@�S�̌��q�̏ꍇ�́A�X�s�����C���[�����g�̒ލ����Ђǂ�����Ă���A���q�P�P�������Ȏ��ƂȂ��Ă���A���̋����͂��ׂĂ̌��f�̌��q�Ȃ��ň�ԋ�
���̂ł��B�S�̌��q�́A�����̊i�q�_�ɌŒ肳��ē������Ƃ��ł��܂��A���̌����͎��R�ɕς�A���낢��̕����������܂��B�S�̖_���������Ď��ɂ���
�Ƃ����̂́A�ł��邾����������̌��q�̎���̕�������s�ɂ��낦�邱�Ƃɂق��Ȃ�܂���B
�@����͂����傴���ςɂ����ƁA�S���q�̓d�q�X�s���ɂ�鎥�C���[�����g�́A�ߐڂ��錴�q�Ԃł́A�݂��ɋt�����������s�̕����G�l���M�[���Ⴍ�Ȃ�悤�ȑ��ݍ�p�������Ă��邽�߂ł��B�i�}�P�O�D�S�D�Q���j
�������łȂ��Ȃ�
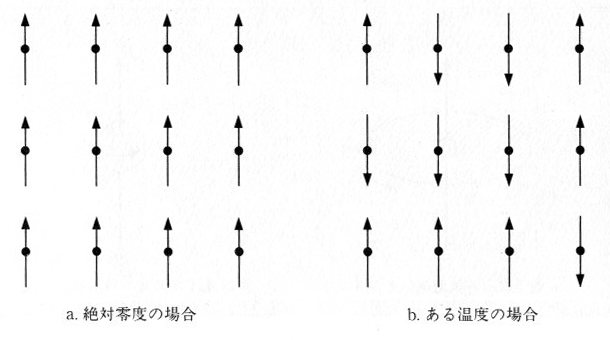
�@�Ƃ��낪���x����������ƁA���q�͂������ɖ������ɂȂ�A������������̃X�s���̌��q��������܂��B�����Ă��鉷�x�i�s�G���E�L�����[�����������B
�L�����[���x�Ƃ����j���z���ƁA���������ɂȂ�A�S�S�̂̎��C���[�����g�͂قڗ�ɂȂ�A�S�͎��łȂ��Ȃ��Ă��܂��̂ł��i�}�P�O�D�S�D�Q���j�B
���̂��Ƃ��A�������̂���̑��]�ڂƂ����܂��B�V�~�����[�V�����ɂ��A���̑��]�ڂ̎��������Ă݂܂��傤�B
| �}�P�O�D�S�D�Q�@��Η�x�̏ꍇ�Ƃ��鉷�x�̏ꍇ�̃X�s�����C���[�����g |
 |
�C�W���O�E���f��
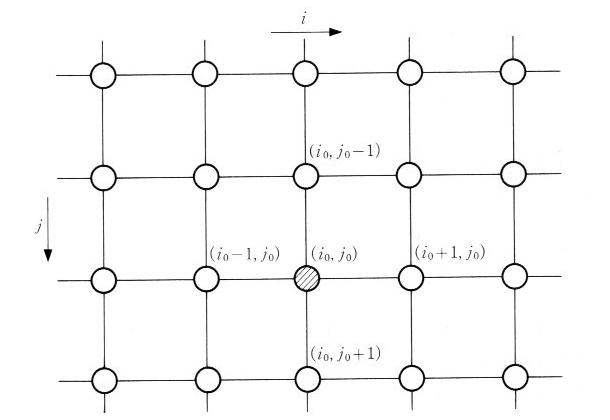
�@�����q���}�P�O�D�S�D�R�̂悤�ɂQ�����i�q��ɕ���ł���Ƃ��܂��B���q
(i,j) �̏�Ԃ́A�X�s������������A���������Ƃ����Q�̏�Ԃ������Ƃ���̂Ƃ��A�����
s(i, j)=1 , s(i, j)= -1 �Ƃ��܂��B���̒l���X�s���ϐ��Ƃ����܂��B
�@���錴�q (i0, j0) ���A�܂��̌��q�����G�l���M�[�́A�܂��̌��q�̃X�s���̕����ƁA�����̃X�s���̕����ɂ���Č��܂�A���̒l�́A
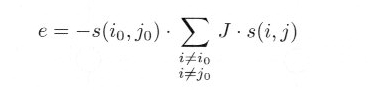 |
�E�E�E�E�E |
���P�O�D�S�D�P |
�ƂȂ�܂��B J �͕����ɂ���ĈقȂ�A (i0, j0) ���痣���ɂ��������ď����Ȓl�ƂȂ�܂��B���Ɍ��q (i0, j0) ���猩�Ă����ׂ�̌��q����̂ݑ��ݍ�p����Ƃ���A���́A
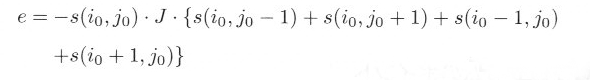 |
|
|
| �E�E�E���P�O�D�S�D�Q |
|
|
�ƂȂ�܂��B e �̒l�́A���q (i0, j0) ���猩�āA�܂��̌��q�̃X�s���̕������S���t�ł���A��ԑ傫���A�܂����q
(i0, j0) �Ƃ܂��̌��q�̃X�s�����S�������ł���A��ԏ������Ȃ�܂��B
�@���鉷�x�ŁA���q (i0, j0) �������]����m���́A���v�͊w�̋�����Ƃ���ɂ��A�P�ʎ��Ԃ�����A
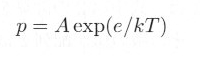 |
�E�E�E�E�E |
���P�O�D�S�D�R |
�ƂȂ�܂��B�����ŁA k �̓{���c�}���萔�A T �͐�Ή��x�A e �͎��̒l�A A �͒萔�ł��B
�@���P�O�D�S�D�Q�ƁA���P�O�D�S�D�R����A���q (i0, j0) �����]����m���́A T �������Ȃ�ƍ����Ȃ�A�t�����̌��q�ɂƂ肩���܂�Ă���Ƃ��ł������A�܂��̌��q�Ɠ��������̂Ƃ��ł��Ⴍ�Ȃ�܂��B
�@���̂悤�ȃ��f�����Ď҂̖��O���Ƃ��āA�C�W���O�E���f���Ƃ����܂��B
| �}�P�O�D�S�D�R |
 |
�v���O�����̃|�C���g
�@�ȏ�̃��f�����A�V�~�����[�V�����ɂ��������܂��i�v���O����s1040.c�j�B���x�������ɂ���ƁA�����炱����ŁA�����ɔ��]���N����܂����A�V�~�����[�V�����ł́A���v���~�����A�����_���Ɍ��q��I�яo���A�������܂��B
�@����ɂ͂܂��A���f���̎��̌��q�ɑ�������z���p�ӂ��܂��B�s14�łP�ӂ̑傫�����A MAX+2 �i�l�� 0 ���� MAX+1 �j�̔z������A���̒��� 1 ���� MAX �܂ł��g���܂��B 0 �� MAX+1 �͎��P�O�D�S�D�Q�̌v�Z������Ƃ� i �A j �� 1 �� MAX �̒l���Ƃ����Ƃ��A���ׂ̗�̒l���z����݂͂����Ȃ��悤�ɂ��邽�߂ł��B�����ď�����Ԃ́A��Η�x�Ƃ����ׂĎ��C���[�����g�͓������A���Ȃ킿
s(i,j)=1 �Ƃ��܂��B
�@���ɍs47�C�s48�łQ�P�g�� �P ���� �l�`�w �܂ł̐����l���Ƃ��l���z�̗����������܂��B���̂P�g�̗����ɂ��A���q���P�I�сA���P�O�D�S�D�Q�̑��ݍ�p�̃G�l���M�[���v�Z���i�s49�j�A���P�O�D�S�D�R�̔��]�̊m�����v�Z���܂��i�s50�j�B������
w0 = kT/J �Ƃ����Đ��K�����x�Ƃ��Ă��܂��B�܂� A = exp(-4/w0) �Ƃ��܂��B�ʂɔ������������Ƃ��̊m�����ׁi�s51�j�A�����̕�����������A���q�]�����܂��i�s52�j�B���̏����� �l�`�w�~�l�`�w ��J��Ԃ��ƁA�e���q�ɂ��āA���ςP�����s�������ƂɂȂ�̂ŁA�N���b�N���P�i�߂܂��B
�A�E�g�v�b�g
�@ s(i, j)=1 �ł��錴�q�̐��𐔂��āA���������v�Z���܂��i�s62�j�B�������͑S���̌��q�� s(i, j)=1 �ł���P, �P�Ɓ|�P�����X�ł���O�̒l�����܂��B�܂��A�f�B�X�v���C�ɁA���X�ƌ��q�̔��]�̗l�q���v���b�g�����܂��B����ɂ͔��]�̂��т�
s(i, j) ���P�̎��͐A�|�P�̎��͐Ԃŕ\�����܂��B����ɂ��~�N���Ȍ��q�̓������p�^�[���Ƃ��Ď��o�ɑi���邱�Ƃ��ł��܂��B
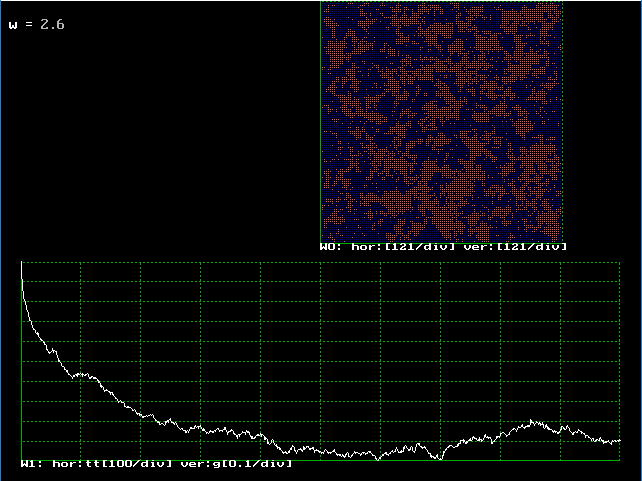
�@�v���O���������s���Ă݂܂��傤�B�}�P�O�D�S�D�S�̂悤�ɐ�Η�x�ł́A��ʂɐ��̃��[�����g�i�}�ł͐j�ł��������̂��A�������ɕ��̃��[�����g�̕����i�}�ł͐ԁj���ł��A���Ԃ̌o�߂ƂƂ��ɂ��ꂪ���̂��i��������C�h���C���Ƃ����܂��j�A�`�����X�ω����Ă����܂��B
�@�E�B���h�E�P�̃O���t�́A������������킵�܂��B
�@���鉷�x�i�L�����[�_�j�ȉ��ł́A�������͂O�ɂȂ炸���̂܂܂ŁA���鉷�x
Tc ��������ƁA���]�ڂ��N���莥�������O�ƂȂ�A�������łȂ��Ȃ��Ă����܂��B���̎��̐��K�����x�́A���_�l�́A
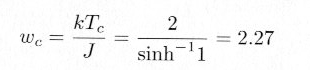 |
�E�E�E�E�E |
���P�O�D�S�D�S |
�ŗ^�����܂��B �v���O�����ł͐��K�����xw0 ��ς��邱�Ƃ��ł���悤�ɂȂ��Ă��܂�����A wc �𒆐S�ɐF�X�ς��đ��]�ڂ��N����l�q���������Ă݂ĉ������B
| �}�P�O�D�S�D�S�@�C�W���O���f���@�V�~�����[�V�������� |
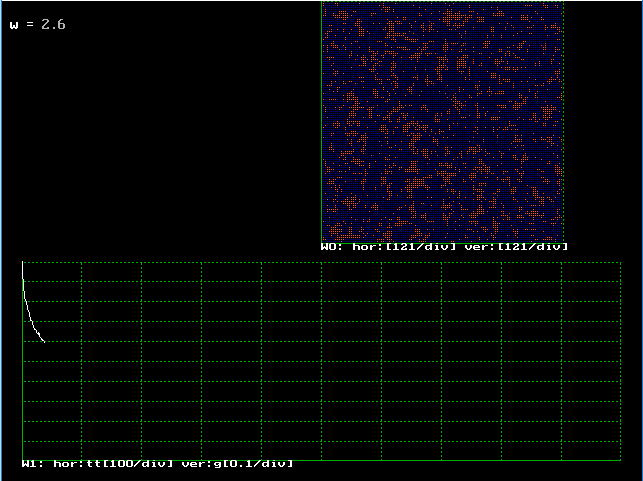 |
| �������ɕ��̃��[�����g�̕����������i�}�ł͐ԁj |
 |
| ���Ԃ̌o�߂ƂƂ��ɁA�����߂����߂��Ȃ��炻�ꂪ���̂��Ă��� |
| �@ s1040.c �@ �C�W���O���f�� |
/* s1040.c
* �C�W���O���f��
* (C) H.Ishikawa 1994 2018
*/
#include <math.h> /* exp() */
#include "compati.h"
#include "window.h"
#define MAX 120 /* �z��̑傫�� */
#define T_END 1000 /* �V�~�����[�V�������I��鎞�� */
int s[MAX+2][MAX+2]; /* ���C���[�����g�̒l
s[i][j]=1���邢��s[i][j]=�1 */
int i,j; /* ���ڂ��Ă��錴�q�̔ԍ� */
int e; /* ���ݍ�p�̒l */
int m; /* s[i][j]=1�ł��錴�q�̐� */
int n; /* for�̃J�E���^ */
int tt = 0; /* �V�~�����[�V�����̎��� */
double p; /* ���]�̊m�� */
double g; /* ������ */
double w; /* ���x�̑��Βl */
int main(void)
{
/* ���� */
opengraph();
SetWindow(0, 0,0,MAX,MAX, WIDTH/2,MAX*2,WIDTH/2+MAX*2,0);
Axis(0, "", MAX, "", MAX);
SetWindow(1, 0,0.0,T_END,1.0, SPACE,HIGHT-SPACE,WIDTH-SPACE,MAX*2+SPACE);
Axis(1, "tt", T_END / 10.0, "g", 0.1);
MoveTo(1, 0, 1.0);
w = 2.8; /*���̒l��ύX���Ď���*/
m = MAX * MAX;
for (j = 0; j <= MAX ; j ++) {
for (i = 0; i <= MAX ; i ++) {
s[i][j] = 1;
}
}
/* ���C�� */
while (tt <= T_END) {
for (n = 1; n <= MAX * MAX; n ++) {
i = (int)(MAX * RAND()) + 1; /* 1����MAX�܂ł̗��� */
j = (int)(MAX * RAND()) + 1;
e = -s[i][j] * (s[i][j - 1] + s[i][j + 1] + s[i - 1][j] + s[i + 1][j]);
p = exp((e - 4.0) / w); /* ���]�m�� */
if ( p > RAND()) {
s[i][j] = -s[i][j]; /* ���] */
m = m + s[i][j];
}
if (s[i][j] == 1) {
PutPixel(0, i, j, 1); /* �� */
} else {
PutPixel(0, i, j, 12); /* ���邢�� */
}
}
tt = tt + 1;
g = (double)(2 * m) / (double)(MAX * MAX) - 1.0;
setcolor(15);
LineTo(1, tt, g);
}
getch();
closegraph();
return 0;
}
|
�W�F�l�e�B�b�N�E�A���S���Y���Ƃ�
�@�W�F�l�e�B�b�N�E�A���S���Y���i�f�`�j�͈�`�I�A���S���Y���Ƃ����A�����̐i���ߒ����V�~�����[�V�������邱�Ƃɂ���āA��������̑g�ݍ����̂Ȃ�
����œK�ȉ��������o����@�̂��Ƃ������܂��B�_�[�E�B���̎��R�������_�Ƃ����̂�����܂����A�������b�ɁA�����̐i���ߒ����H�w�I���f���ɂ�������
�����̂ł��B
�@�i���ߒ��̊T�v�́A�����悻���̂悤�ɂ���킳���ł��傤�B�܂��A�O�ƂP�̒l������`�q(Gene)����Ȃ���F�́iChromosome)���l��
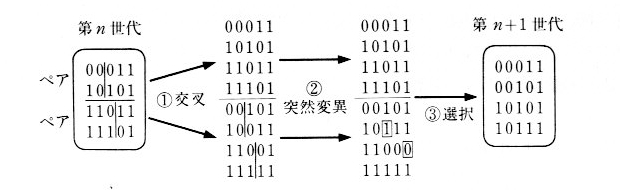
�܂��B���̐��F�̂̂��܂���W�c(Population)�Ƃ����܂��B����ɑ��}�P�O�D�T�D�P�悤�Ɂi�P�j�A�i�Q�j�A�i�R�j�̑�����قǂ����܂��B
�i�P�j�@����
�@�W�c���̂Q�̐��F�̂̑g�i�y�A�j�ɂ����āA����(crossover)�Ƃ�����`�q�̈ꕔ�̓���ւ��������Ȃ��邱�ƁB
�i�Q�j�@�ˑR�ψ�
�@�e���F�̂ɂ����āA����m���ŁA��`�q�̈ꕔ���O����P���邢�́A�P����O�ɕԓ]���邱�ƁB
�i�R�j�@�I��
�@�i�P�j�A�i�Q�j���ւ���`�q�����������F�̂̂������ւ̂�荂���K�����������̂��A�I������邱�ƁB
�i�P�j�A�i�Q�j�A�i�R�j�̈�`�q�I������P����Ƃ�сA���̑�������肩�����Ă����ƁA���̏W�c�͂����ɏ�����������ɐi�����܂��B
�@�W�F�l�e�B�b�N�E�A���S���Y���ł́A���܂��܂ȑg�ݍ��킹����`�q����Ȃ���F�̂ŕ\�����A���̑g�ݍ��킹���Ƃ̖ړI�����v�Z���܂��B�����āA���̒l
�̍������̂�I�����A������c���悤����������������ɂ��킽��s�킹��A�ŏI�I�ɂ́A�ړI���̒l���ő�ƂȂ�悤�ɂ��邱�Ƃ��ł��܂��B
�@�W�F�l�e�B�b�N�E�A���S���Y���̌����́A�����قǒP���ł����A���̒T���\�͔͂��ɍ����A�ʏ�̕��@�ł͉��������ɂ����ꍇ�ł��A��r�I�e�Ղɐ��m�ɋ߂Â����Ƃ��ł���Ƃ����Ă��܂��B
| �}�P�O�D�T�D�P�@�g�ݑւ��i�����ƓˑR�ψفj |
 |
�i�b�v�U�b�N���
�@�W�F�l�e�B�b�N�E�A���S���Y���̃��J�j�Y�����u�i�b�v�U�b�N���v�Ƃ����T�^�I�ȑg�ݍ��������ɁA�v���O����������Ă݂܂��傤�B
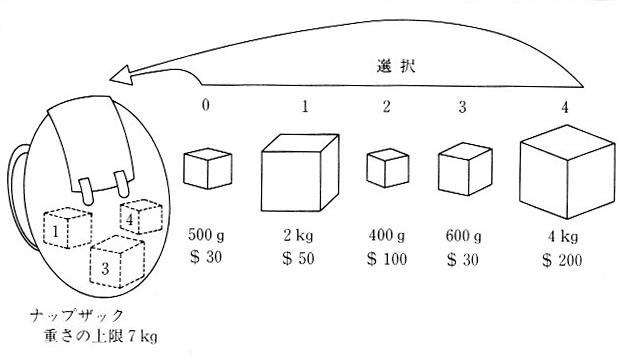
�@�}�P�O�D�T�D�Q�̂悤�ɁA�i�b�v�U�b�N������܂��B�i�b�v�U�b�N�ɂ͂��ׂ�d���ɂ͌��E������܂��B��������̈قȂ�d���́A�قȂ鉿�l�����i�����^
����ꂽ�Ƃ��A�d�����i�b�v�U�b�N�̌��E�l���ŕi��������I�����A���̎��̉��l�̍��v���ő�ƂȂ�悤�ȑg�ݍ�����������Ƃ������ł��B���Ȃ킿�A
���̏ꍇ�̖ړI���͉��l�̍��v�ŁA�i�b�v�U�b�N�������Ȃ��͈͂ŁA���l���ł������Ȃ�悤�A�i����I��ʼn^�ڂ��Ƃ�����̂ł��B�ʏ�̕��@�ł͉��������ɂ�����ł��B
| �}�P�O�D�T�D�Q�@�i�b�v�U�b�N�̖�� |
 |
�i�b�v�U�b�N���̃v���O����
�@�i�b�v�U�b�N�����A�W�F�l�e�B�b�N�E�A���S���Y���̎�@�ʼn����ꍇ�A�܂��A�i�b�v�U�b�N�ɕi���������Ă����Ԃ���F�̂ɑΉ������āA�\������K�v������܂��B�}�P�O�D�Q�D�T�̗�ł́A�i���P�A�R�A�S���i�b�v�U�b�N�ɓ���Ă����Ԃł�����A�������F�̂�
�@�@�@�@�O�P�O�P�P
�ƕ\�����܂��B
�@�v���O����s1050.c�ɂ��Đ������Ă����܂��BLENGTH�Ƃ��������������F�̂�SIZE�p�ӂ��܂��B���ۂɂ͑g�ݑւ�����̂��߁C���̂Q�{�̔z����s19�ɂ��p�ӂ��܂��B�܂��C�s20�ɂ��V����̐��F�̂�\�킷�z����������܂��B���̂ق��P�P�̕i���̏d�ʁC���l������킷�z��C���F�̂ɑΉ������d�ʂ̍��v�C���l�̍��v������킷�z���p���܂��B
�@�s50����s56�܂łŐ��F�̂�������Ԃɂ��܂��BPROB2�̊m���łP�ɃZ�b�g���C�܂��s59����s62�ɂ����āC�e�i�����Ƃ̏d�ʂƉ��l�������ŃZ�b�g���Ă����܂��B
�@�s65���炪���C���̎n�܂�ŁC��`�q�̑g�ݑւ��i�����ƓˑR�ψفj�C�ړI���̌v�Z�C�\�[�g�C�V����ւ̂��������C�\���Ƃ����葱�����CG_END�Ŏ�����鐢��ɂ킽���ČJ��Ԃ��v�Z���܂��B
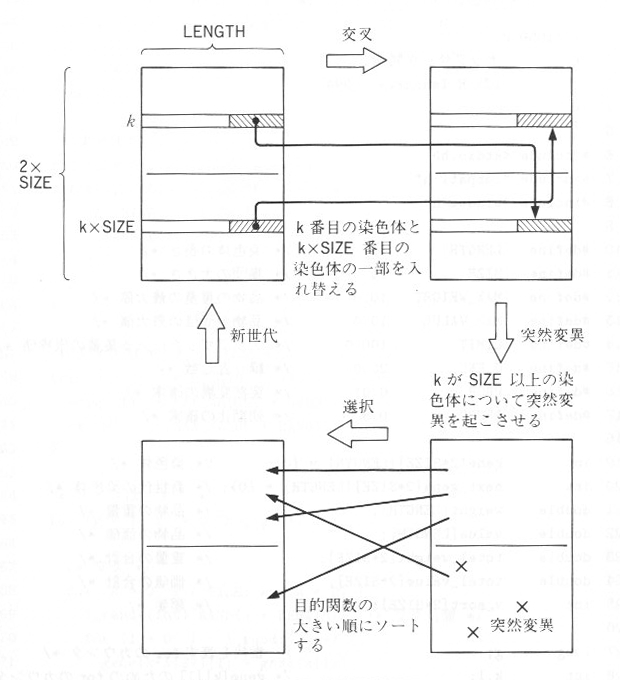
�@��`�q�̑g�ݑւ��́C�}�P�O�D�T�D�R�̂悤�ɍs���܂��Bk�Ԗڂ̐��F�̂ƁCk+SIZE�Ԗڂ̐��F�̂��y�A�ł���Ƃ��āC�����̑�����s���܂��B�s69�̂悤�Ɍ����ʒu�𗐐��Ŕ��������Ck�Ԗڂ̌㔼��k+SIZE�Ԗڂ̌㔼����ꊷ���܂��B���ɍs85�ȉ��̂悤��k�̒l��SIZE�ȏ�̐��F�̂ɂ���PROB�Ƃ����m���ŁC�P�ƂO�]�����C�ˑR�ψق��N�������܂��B
�@���ɁC�ړI�����v�Z���܂��B�ړI���́C���F�̂��Ƃ́C���v�̏d�ʂƍ��v�̉��l�ł��Bgene[k][l]�ɑI�ꂽ�i���̑g�ݍ�����������Ă��܂�����C�s98���邢�͍s99�̂悤�ɁC���̔z��ɏd�ʁC���邢�͉��l�̔z��������C���v�̏d�ʁC���l���v�Z���܂��B���̏ꍇ�C�d�ʂ̍��v���C�i�b�v�U�b�N�̏d�ʂ̏��LIMIT���������ꍇ�C�s102�ɂ�艿�l���[���Ƃ��C���̐��F�̂��I������Ȃ��悤�ɂ��܂��B
�@���ɁC�s107�ȉ��̂悤�ɁC���l�̍��v��傫�����Ƀ\�[�g���܂��B�\�[�g�̃A���S���Y���͂��܂��܂Ȃ��̂�����܂����C�����ł́C�ȒP�ȑI��@�Ƃ����A���S���Y����p���܂��Btotal_value[k]�ɂ��āC�܂��Ck���Œ肵�Ck+1�ȉ��̂��̂Ɣ�r���C���傫�����̂�����C����ƒu�������܂��B�����āCk�����X���₵�čs���ƁCtotal_value[k]���傫�����ɕ��т܂��B�܂��Cv_sort�k]�ɁC0,1,2,3,����̒l�����Ă����ƁC���̃\�[�g���I�������Ԃ�v_sort[k]��,total_value[k]�̑傫�������珇�Ԃ̒l������܂��B
�@�\�[�g�̌��ʂ�����v_sort[k]�ɂ��C�s126�̂悤�ɁC�傫�����ɁCgene[k][l]�����o���C�����V�����next_gene[k][l]�̐��F�̂����C�s131�ɂ��gene[k][e]����ꊷ���܂��B
�@
| �}�P�O�D�T�D�R�@��`�q�̑g�݊��� |
 |
���ʂ̏o��
�@�Q�̃E�C���h�E�ɉ�������A�c�����ꂼ��d�ʂ̍��v�A���l�̍��v���O���t�\�����܂��B�܂��A�����Ƃ��ړI���̑傫�� k = 0 �̐��F�̂̍\���A�܂����̂Ƃ��̏d�ʂ̍��v�A���l�̍��v��\�����܂��B
�@���̃v���O�����𑖂点��ƁA�}�P�O�D�T�D�S�̂悤�ɁA�P�O�O����قǂŁA�œK�ɋ߂��l�������Ă��܂����A�P�O�O�O���キ�肩�������s����K�v������܂��B
| �}�P�O�D�T�D�S�@�i�b�v�U�b�N���@�V�~�����[�V�������� |
 |
| �@ s1050.c �@�@ �i�b�v�U�b�N��� |
/* s1050.c
* �i�b�v�U�b�N���
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h>
#include "compati.h"
#include "window.h"
#define LENGTH 40 /* ���F�̂̒��� */
#define SIZE 10 /* �W�c�̑傫�� */
#define MAX_WEIGHT 10.0 /* �i���̏d�ʂ̍ő�l */
#define MAX_VALUE 10.0 /* �i���̉��l�̍ő�l */
#define LIMIT 100.0 /* �i�b�v�U�b�N�ɓ���d�ʂ̌��E�l */
#define G_END 2000 /* �J��Ԃ��� */
#define PROB 0.01 /* �ˑR�ψق̊m�� */
#define PROB2 0.5 /* �������̊m�� */
int gene[2*SIZE][LENGTH] = {0}; /* ���F�� */
int next_gene[2*SIZE][LENGTH] = {0}; /* �V����̐��F�� */
double weight[LENGTH]; /* �i���̏d�� */
double value[LENGTH]; /* �i���̉��l */
double total_weight[2*SIZE]; /* �d�ʂ̍��v */
double total_value[2*SIZE]; /* ���l�̍��v */
int v_sort[2*SIZE]; /* ���� */
long g; /* �����\��for�̃J�E���^ */
int k,l; /* gene[k][l]�̂��߂�for�̃J�E���^ */
int l_rand; /* �����ʒu */
int k_sort; /* �\�[�g�p��for�̃J�E���^ */
int i_swap; /* �X���b�v�p�ϐ� */
double swap; /* �X���b�v�p�ϐ� */
int main(void)
{
/* �O���t�B�b�N�̏��� */
opengraph();
SetWindow(0, 0.0,0.0,G_END,120,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "generation", G_END / 10, "weight", 20);
MoveTo(0, 0.0, 0.0);
SetWindow(1, 0.0,0.0,G_END,250,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "generation", G_END / 10, "value", 50);
MoveTo(1, 0.0, 0.0);
setlinestyle(0, 0, 2);
srand(3);
/* ���F�̂̃C�j�V�����C�Y */
for (k = 0 ; k < SIZE; k ++) {
for (l = 0; l < LENGTH; l ++) {
if (RAND() < PROB2){
gene[k][l] = 1;
}
}
}
/* �i���̏d���Ɖ��l�̐ݒ� */
for (l = 0; l < LENGTH; l ++) {
weight[l] = MAX_WEIGHT * RAND();
value[l] = MAX_VALUE * RAND();
}
/* ���C���n�܂� */
for (g = 1; g <= G_END; g ++) {
/* ���� */
for (k = 0; k < SIZE; k = k + 2) {
l_rand=(int)(RAND() * LENGTH); /* �����ʒu */
for (l = 0; l < l_rand; l ++) {
gene[k+SIZE][l] = gene[k][l];
}
for (l = l_rand; l < LENGTH; l ++) {
gene[k+SIZE][l] = gene[k+1][l];
}
for (l = 0; l < l_rand; l ++) {
gene[k+1+SIZE][l] = gene[k+1][l];
}
for (l = l_rand; l < LENGTH; l ++) {
gene[k+1+SIZE][l] = gene[k][l];
}
}
/* �ˑR�ψ� */
for (k = SIZE ; k < 2 * SIZE; k ++) {
for (l = 0; l < LENGTH; l ++) {
if (RAND() < PROB) {
gene[k][l] = 1 - gene[k][l];
}
}
}
/* �ړI���̌v�Z */
for (k = 0; k < 2 * SIZE; k ++) {
total_weight[k] = 0.0;
total_value[k] = 0.0;
for (l = 0; l < LENGTH; l ++) {
total_weight[k] = total_weight[k] + gene[k][l] * weight[l];
total_value[k] = total_value[k] + gene[k][l] * value[l];
}
if (total_weight[k] > LIMIT) {
total_value[k] = 0.0;
}
}
/* �\�[�g */
for (k = 0; k < 2 * SIZE; k ++) {
v_sort[k] = k;
}
for (k = 0; k < 2 * SIZE; k ++) {
for (k_sort = k + 1; k_sort < 2 * SIZE; k_sort ++) {
if (total_value[k] < total_value[k_sort]) {
swap = total_value[k_sort];
total_value[k_sort] = total_value[k];
total_value[k] = swap;
i_swap = v_sort[k_sort];
v_sort[k_sort] = v_sort[k];
v_sort[k] = i_swap;
}
}
}
/* �V����ɂ������� */
for (k = 0; k < 2 * SIZE; k ++) {
for (l = 0 ;l < LENGTH; l ++) {
next_gene[k][l] = gene[v_sort[k]][l];
}
}
for (k = 0; k < 2 * SIZE; k ++) {
for (l = 0; l < LENGTH; l ++) {
gene[k][l] = next_gene[k][l];
}
}
/* �\�� */
gotoxy(1,1); printf(" %5d ",g);
for (l = 0; l < LENGTH; l ++) {
printf("%1d", gene[k][l]);
}
printf(" %8.3f %8.3f\n", total_weight[v_sort[0]], total_value[0]);
LineTo(0, g, total_weight[v_sort[0]]);
LineTo(1, g, total_value[0]);
}
getch();
closegraph();
return 0;
}
/* s1050.c
* �i�b�v�U�b�N���
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h>
#include "compati.h"
#include "window.h"
#define LENGTH 40 /* ���F�̂̒��� */
#define SIZE 10 /* �W�c�̑傫�� */
#define MAX_WEIGHT 10.0 /* �i���̏d�ʂ̍ő�l */
#define MAX_VALUE 10.0 /* �i���̉��l�̍ő�l */
#define LIMIT 100.0 /* �i�b�v�U�b�N�ɓ���d�ʂ̌��E�l */
#define G_END 2000 /* �J��Ԃ��� */
#define PROB 0.01 /* �ˑR�ψق̊m�� */
#define PROB2 0.5 /* �������̊m�� */
int gene[2*SIZE][LENGTH] = {0}; /* ���F�� */
int next_gene[2*SIZE][LENGTH] = {0}; /* �V����̐��F�� */
double weight[LENGTH]; /* �i���̏d�� */
double value[LENGTH]; /* �i���̉��l */
double total_weight[2*SIZE]; /* �d�ʂ̍��v */
double total_value[2*SIZE]; /* ���l�̍��v */
int v_sort[2*SIZE]; /* ���� */
long g; /* �����\��for�̃J�E���^ */
int k,l; /* gene[k][l]�̂��߂�for�̃J�E���^ */
int l_rand; /* �����ʒu */
int k_sort; /* �\�[�g�p��for�̃J�E���^ */
int i_swap; /* �X���b�v�p�ϐ� */
double swap; /* �X���b�v�p�ϐ� */
int main(void)
{
/* �O���t�B�b�N�̏��� */
opengraph();
SetWindow(0, 0.0,0.0,G_END,120,
SPACE,HIGHT/2-SPACE/2,WIDTH-SPACE,SPACE);
Axis(0, "generation", G_END / 10, "weight", 20);
MoveTo(0, 0.0, 0.0);
SetWindow(1, 0.0,0.0,G_END,250,
SPACE,HIGHT-SPACE,WIDTH-SPACE,HIGHT/2+SPACE/2);
Axis(1, "generation", G_END / 10, "value", 50);
MoveTo(1, 0.0, 0.0);
setlinestyle(0, 0, 2);
srand(3);
/* ���F�̂̃C�j�V�����C�Y */
for (k = 0 ; k < SIZE; k ++) {
for (l = 0; l < LENGTH; l ++) {
if (RAND() < PROB2){
gene[k][l] = 1;
}
}
}
/* �i���̏d���Ɖ��l�̐ݒ� */
for (l = 0; l < LENGTH; l ++) {
weight[l] = MAX_WEIGHT * RAND();
value[l] = MAX_VALUE * RAND();
}
/* ���C���n�܂� */
for (g = 1; g <= G_END; g ++) {
/* ���� */
for (k = 0; k < SIZE; k = k + 2) {
l_rand=(int)(RAND() * LENGTH); /* �����ʒu */
for (l = 0; l < l_rand; l ++) {
gene[k+SIZE][l] = gene[k][l];
}
for (l = l_rand; l < LENGTH; l ++) {
gene[k+SIZE][l] = gene[k+1][l];
}
for (l = 0; l < l_rand; l ++) {
gene[k+1+SIZE][l] = gene[k+1][l];
}
for (l = l_rand; l < LENGTH; l ++) {
gene[k+1+SIZE][l] = gene[k][l];
}
}
/* �ˑR�ψ� */
for (k = SIZE ; k < 2 * SIZE; k ++) {
for (l = 0; l < LENGTH; l ++) {
if (RAND() < PROB) {
gene[k][l] = 1 - gene[k][l];
}
}
}
/* �ړI���̌v�Z */
for (k = 0; k < 2 * SIZE; k ++) {
total_weight[k] = 0.0;
total_value[k] = 0.0;
for (l = 0; l < LENGTH; l ++) {
total_weight[k] = total_weight[k] + gene[k][l] * weight[l];
total_value[k] = total_value[k] + gene[k][l] * value[l];
}
if (total_weight[k] > LIMIT) {
total_value[k] = 0.0;
}
}
/* �\�[�g */
for (k = 0; k < 2 * SIZE; k ++) {
v_sort[k] = k;
}
for (k = 0; k < 2 * SIZE; k ++) {
for (k_sort = k + 1; k_sort < 2 * SIZE; k_sort ++) {
if (total_value[k] < total_value[k_sort]) {
swap = total_value[k_sort];
total_value[k_sort] = total_value[k];
total_value[k] = swap;
i_swap = v_sort[k_sort];
v_sort[k_sort] = v_sort[k];
v_sort[k] = i_swap;
}
}
}
/* �V����ɂ������� */
for (k = 0; k < 2 * SIZE; k ++) {
for (l = 0 ;l < LENGTH; l ++) {
next_gene[k][l] = gene[v_sort[k]][l];
}
}
for (k = 0; k < 2 * SIZE; k ++) {
for (l = 0; l < LENGTH; l ++) {
gene[k][l] = next_gene[k][l];
}
}
/* �\�� */
gotoxy(1,1); printf(" %5d ",g);
for (l = 0; l < LENGTH; l ++) {
printf("%1d", gene[k][l]);
}
printf(" %8.3f %8.3f\n", total_weight[v_sort[0]], total_value[0]);
LineTo(0, g, total_weight[v_sort[0]]);
LineTo(1, g, total_value[0]);
}
getch();
closegraph();
return 0;
}
|
�P�D�P�O�D�P�߂̃N���b�v�X�͓������L���ȃQ�[���ł��B�����Ă������Ă��A����P�h�����q���������ꍇ�A�ǂ̂��炢�̉Ńv���[�����j�Y���邩�m���߂Ȃ����B
�@�@�i�j�@
| �@ a1010.c �P�O�͂P�D�� |
/* a1010.c �P�O�͂P�D��
* �N���b�v�X
* (C) H.Ishikawa 1994 2018
*/
#include <time.h> /* time() */
#include "compati.h"
#include "window.h"
#define T_END 10000 /* �����Ԃ���Ă݂� */
long t; /* �N���b�N */
long q = 100; /* ������ */
long k = 1; /* �P��̓q�� */
int dice(void);
int craps(void);
int main(void)
{
opengraph();
SetWindow(0, 0.0,0.0,(double)T_END,200.0,
SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "t", T_END/10, "q", 100);
MoveTo(0, 0.0, q);
srand((unsigned)time(NULL)); /* �V�~�����[�V�����̓s�x�����n���ς��� */
for (t = 1; t <= T_END; t ++) {
q = q - k;
if (craps() == 1) { /* �������ꍇ */
q = q + 2 * k;
k = 1; /* �P�h���q���� */
}
LineTo(0, (double)(t), (double)(q));
if (q == 0) { break; } /* �j�Y������~�܂� */
}
getch();
closegraph();
return 0;
}
int dice(void)
{
return((int)(RAND() * 6.0 + 1));
}
int craps(void)
{
int r; /* 1:���� 0:���� */
int sum1; /* �a�P */
int sum2; /* �a�Q */
sum1 = dice() + dice();
if (sum1 == 7 || sum1 == 11) { /* �i�`������ */
r = 1;
} else if(sum1 == 2 || sum1 == 3 || sum1 == 12) { /* �N���b�v�X */
r = 0;
} else {
sum2 = 0;
r = 0;
while (sum2 != 7) { /* �V���o��܂� */
sum2 = dice() + dice();
if (sum2 == sum1) { /* �|�C���g */
r = 1;
break;
}
}
}
return(r);
}
|
�Q�D�@�P�O�D�Q�߂̍ɊǗ����ł́A�����_����������ɔ������Ă������A���T�P��莞�ɓ��ׂ�����Ƃ��āA���̓��חʂ�O�X���̍ɗʂɂ�茈�肵�A����ɂ�蔭��������@�ɂ��āA�V�~�����[�V�������A�œK���חʁ@�����߂Ȃ����B
�@�@�i�j�@
| �@ a1020.c �P�O�͂Q�D�� �@ �ɊǗ��̖�� �@�i������ׁj |
/* a1020.c �P�O�͂Q�D��
* �ɊǗ��̖�� �@�i������ׁj
* (C) H.Ishikawa 1994 2018
*/
#include <stdio.h>
#include <math.h>
#include "compati.h"
#include "window.h"
#define FRIDAY 4 /* ���ד��͋��j�� */
#define AL 5 /* �P���̕��ϔ���� */
#define SP 7000.0 /* ���l */
#define PC 5000.0 /* �d����P�� */
#define C1 20.0 /* �P���P������̍ɔ�p */
#define C2 10000.0 /* �P��̔����ɂƂ��Ȃ���p */
#define C3 500.0 /* �i��P������̑��� */
#define T_END 10000
#define A1_MIN 20
#define A1_MAX 200
long poisson(double lambda);
int main(void)
{
long tt; /* �V�~�����[�V�������� */
long a; /* �P��̓��ח� */
long q; /* ���ݍɗ� */
long a1; /* �������f�� */
long k; /* �P���̔���� */
long zk; /* k�̗v */
long yk; /* ������̗v */
long ls; /* �Ɋ���̂��ߔ��葹�Ȃ����� */
long nn; /* ������ */
double sc1; /* �ɔ�p�̗v */
double sc2; /* ������p�̗v */
double sc3; /* �i�ꑹ���̗v */
double rr; /* ������ */
/* �O���t�B�b�N���� */
opengraph();
SetWindow(0, 0.0,0.0,A1_MAX,1.0e08,
SPACE,HIGHT-SPACE,WIDTH-SPACE,SPACE);
Axis(0, "q1", 10, "rr", 1e07);
setlinestyle(0, 0, 2);
printf(" a1 yk ls nn sc1 sc2 sc3 rr\n");
/* �J�n */
for (a1 = A1_MIN; a1 <= A1_MAX; a1 = a1 + 10) {
/* �����ݒ� */
srand(113);
tt = 0; q = a1; zk = 0; ls = 0; nn = 0;
sc1 = 0.0; sc2 = 0.0; sc3 = 0.0;
/* �P���� */
while (tt <= T_END) {
k = poisson(AL); /* k���ꂽ */
q = q - k;
zk = zk + k;
if (q < 0) { /* �Ɋ���̂��ߔ��葹�Ȃ� */
ls = ls - q;
q = 0;
}
if ((tt % 7) == (FRIDAY - 2)) { /* ���חʌ��߂���͋��j�̂Q���O */
a = a1 - q; /* a1�ƍ����̍ɂ̍������� */
if (a <= 0) {
a = 0;
} else {
nn = nn + 1;
}
}
if ((tt % 7) == FRIDAY) { /* ���ד� */
q = q + a;
}
sc1 = q * C1 + sc1;
tt = tt + 1;
}
sc2 = nn * C2;
sc3 = ls * C3;
yk = zk - ls;
rr = (SP - PC) * yk - sc1 - sc2 - sc3;
printf("%4ld %6ld %6ld %6ld %8.0f %8.0f %8.0f %8.0f\n",
a1, yk, ls, nn, sc1, sc2, sc3, rr);
if (a1 == A1_MIN) {
MoveTo(0, a1, rr);
} else {
LineTo(0, a1, rr);
}
}
getch();
closegraph();
return 0;
}
long poisson(double lambda)
{
double xp = RAND();
long k = 0;
while (xp >= exp(-lambda)) {
xp = xp * RAND();
k = k + 1;
}
return (k);
}
|
�R�D�v���O����s1040.c�� w �� wc �𒆐S�ɕς��Ď��s���Ă݂Ȃ����B w �� wc ��菬�����ꍇ�A���������O�ƂȂ炸���̂܂܂ł��邱�Ƃ��������߂Ȃ����B�܂�
w �� wc ���傫���ꍇ�A���������O�ƂȂ鑬�x���������Ƃ��������߂Ȃ����B
�@�@�i�ȗ��j
|
 |
