|
シミュレーションとは
シミュレーションとは何でしょうか。子供の頃、何なにごっこという遊びをしました。本物ではなくまねごとですが、実際の大人になったつもりで、小さな世
界を作りだしていました。シミュレーションはまさにこの”ごっこ”なのです。実際に起るであろうさまざまな事象をコンピュータにまねをさせること、それが
シミュレーションです。
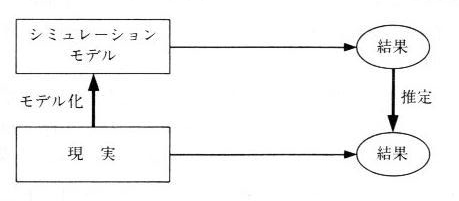
図1.1.1をご覧下さい。まず、現実の現象をモデル化します。そのモデルにしたがって、コンピュータにより、まねのための計算をし、実際の結果を推定
するものです。コンピュータによるシミュレーションによれば、実際の現象があまりに大規模であったり危険が伴うような場合でも、経済的に安全に実験ができ
ます。またソフトウェアによって構成されるので、その条件を任意にかつ簡単に変更でき、融通性に富むという利点があります。シミュレーションの使い方は、
さまざまですが、システムの設計において事前にその特性を評価したり、施策の予測を行い、意志決定に反映させる場合などに用いられます。また最近では、シ
ミュレーションを用いたゲームも、ポピュラーになってきました。
| 図1.1.1 コンピュータシミュレーション |
 |
連続変化モデルと離散変化モデル
コンピュータ・シミュレーションでは、現実をモデル化し、それをコンピュータの上で計算をして結果を得ます。そのモデル化の方法として、シミュレーショ
ンする対象により、連続変化モデルと、離散変化モデルに大きく分けられます。連続変化モデルは、時間経過に伴う事象を微分方程式によって記述します。この
微分方程式をコンピュータによって解くことが、連続変化モデルのシミュレーションです。たとえば、機械系の振動、電気回路の振舞いなどは、微分方程式で記
述できます。
それにたいし、離散変化モデルは、確率的に不規則に起る現象を、コンピュータによって実験し、再現しようとするものです。例えば、放射性原子の寿命を調
べる、公衆電話の待行列の長さを予測する、電話のお話中である確率を調べる、高速道路の料金所でならぶ時間を調査する、コンピュータの内部処理の性能を解
析するなどの問題がこれにあたります。一般に、離散変化モデルのほうが連続変化モデルより、解析が困難な場合が多く、コンピュータ・シミュレーションのあ
りがたみが大きいわけです。この本であつかうシミュレーションの範囲は、おもにこの離散変化モデルのシミュレーションです。
モンテカルロ法
確率的に不規則な現象をコンピュータで再現するには、不規則な数、すなわち乱数を用います。乱数を用いたコンピュータ実験のことをモンテカルロ法という
ことがあります。離散変化モデルのシミュレーションは、モンテカルロ法が基本となっています。モンテカルロ法の最初の例は、18世紀のスランスの自然科学
者
Comte de Buffon
の実験に見られます。5.1節でそれを再現しますが、2本の平行線を引いた平面の上に針を落し、針と平行線の交わる回数を数えることにより、πの値を計算
できるというものです。
また、モンテカルロ法が実用化されたのは、第2次大戦中の研究です。ロスアラモス科学研究所の
John von Neumann
らは、中性子が物質の中を動くさまを知るために、通常の方法では危険で時間がかかりすぎるため、ビュホンの珍奇と思われてきた方法(5.1参照)を、コン
ピュータで再度採用したのです。そしてこのやり方の暗号名を、知的な賭遊びと同じ原理に基づいていることから、モンテカルロ法と呼びました。
離散シミュレーションをもっと手軽に
離散シミュレーションのためには,通常大型コンピュータや,場合によっては,スーパコンピュータが用いられます。それは確率実験の場合,十分な計算時間をかけないと,精度の高い,結果が得られないからです。後でのべるように,1桁の精度を上げるためには,それまでに要した計算の100倍の計算をしなければなりません。ですから手元にある,パーソナル・コンピュータや,ワーク・ステーションでは,とても手におえない範囲のこととされていました。また,離散モデルをうまく記述するためのコンピュータ言語,例えばGPSS,SIMSCRIPTなどは,もっぱら大型コンピュータの上でのみしか,動けませんでした。
この本では,パーソナル・コンピュータあるいはワーク・ステーションを用いて,シミュレーションをおこないます。最近のパーソナル・コンピュータや,ワーク・ステーションの性能向上には目を見張るものがあります。パーソナル・コンピュータについていえば,高速のCPUと,十分なメモリにより,数年前と比べると1桁以上の性能となり,ワーク・ステーションも,大型コンピュータと,なんら性能の差がなくなってきています。また,これらの機器は,手元にあり,占有時間について気にすることなく,場合によっては,一晩中シミュレーションを続けても他の人に迷惑をかけることはありません。さらに,ディスプレイで,途中経過をグラフ表示しながらシミュレーションを進めることができますから,結果の収束状態を監視することができます。
Cを用いる
本書ではシミュレーション・プログラミングにCを用いることとしました。その理由は,まず第一に,Cのコンパイラは,他の言語に比べ実行速度の速いコードを出力するからです。シミュレーションでは,実行速度が最もシビアな問題です。BASICに比べ10倍以上,またPASCALに比べても,ほぼ確実に速い。つぎにCは,構造化プログラミング技術と大変よく適合するということです。Cを使うと,自然にプログラム構造がきちんとなり,デバッグがしやすく,後で読み返しやすいプログラムとなります。第三に,これが最も重要なことかもしれませんが,現在Cが最もポピュラな言語であるということです。とりわけここ数年,Cの人気は爆発的で,たくさんのコンパイラや書籍があり,実用的な,また趣味の領域でも急成長を,遂げています。
しかしながら,Cにも欠点があります。Cは,軽快で融通がきき,拡張性がある反面,逆にそのことが,プログラムの表現に多様性をゆるし,分かりにくくしがちとなります。本書においては,この分かりにくいC独特のいいまわしを,極力避け,BASICや,PASCALの利用者にも,とっつきやすいプログラムとなるよう心がけました。特に,Cの初心者が,つまずきやすい,ポインタ,構造体,共用体は使用しませんでした。また,Cにおいて,もっとも特徴的な,a++というような,表現方法すらも最小限にしました。
簡易ウインドウシステム
画面上のスクリーンにシミュレーションの結果を,グラフにして出力すると,全体が把握できたいへんわかりやすい。ところが,パーソナル・コンピュータやワーク・ステーションのスクリーンは,一般に左上が原点で,右へあるいは,下へ行くほど座標の値が増える方向にあります。いっぽう,物理,数学などで用いるグラフは,原点は左下で,増加方向は,右あるいは,上が通常です。また,一つの,スクリーン上に,二つ以上のグラフを同時に表示できるようにすると大変便利です。簡易なウインドウシステムをつくり,座標変換をあわせて行なうように,"window.h"というヘッダファイルを作りしました。これらの説明は付録にあります。
この本の使い方
この本では,2章でシミュレーションで基本となる,乱数の発生方法,乱数の性質を学びます。3章では乱数を用い,確率的な簡単な実験をおこないます。4章においては,さまざまな分布の乱数を作りシミュレーションに備えます。5章では,シミュレーションの基本となったモンテカルロ・シミュレーションを,実際にプログラミングしてみます。
6章では,ランダムウォークとその応用をのシミュレーションします。7章では通信分野で,進展が大きい信号処理の初歩を,学びます。8章が,本書の最も重要な部分で,同時に進行する,状態変化をシミュレーションする手法を学び,9章でその手法を用い通信トラヒックの問題を解析します。最後にシミュレーションの様々な応用例,ギャンブルからジェネティック・アルゴリズムまでをプログラミングしてみます。
この本は単なる解説の本ではなく,実際にシミュレーションプログラムを作り,動かすことを目的にしています。すべてのプログラムは,リストを用意していますから,それを土台に,自分の問題の解決のためのプログラムを作成して下さい。また各章の終りには,演習問題を用意しましたから,理解を深めるため,挑戦してください。
きっと新しい発見と喜びがあるでしょう。
|
